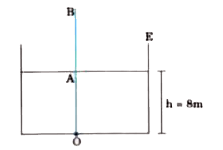
An object O is placed at the bottom of a container in which water is filled up to a height of 8m. Refractive index of water is 4/3. OAB is a vertical line. Observer is looking at O from point E as shown in figure. For the observer, position of O will appear to be
Somewhere on line OAB
To the left of line OAB
At a depth 6m below water surface
At a depth less than 6 m below the water surface
The correct Answer is:B, D
If observer looks from point B then apparent depth would be 84/3=6m. But for the observer at E image will be shifted further away from E in horizontal direction and hence will be on the left side of line OAB. Image will also be shifted a little upward to make apparent depth less than 6m. Hence, options (b) and (d) are correct.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - OBJECTIVE TYPE QUESTIONS (D. MULTIPLE CHOICE QUESTIONS)
5 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - OBJECTIVE TYPE QUESTIONS (ASSERTION REASON TYPE QUESTIONS)
10 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - OBJECTIVE TYPE QUESTIONS (JEE (ADVANCED) FOR IIT ENTRANCE)
20 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
12 Videos
Similar Questions
A coin placed at the bottom of a beaker appears to be raised by 4.0 cm. If the refractive index of water is 4/3, find the depth of the water in the beaker.
View SolutionAn object O is kept in air and a lens of focal length 10cm (in air) is kept at the botton of a container which is filled upto a height 44cm by water. The refractive index of water is 4/3 and that of glass is 3/2. The botton of the container is closed by a thin glass slab of refractive index 3/2. Find the distance (in cm) of the final image formed by the system from botton of container (refer to figure shown below).
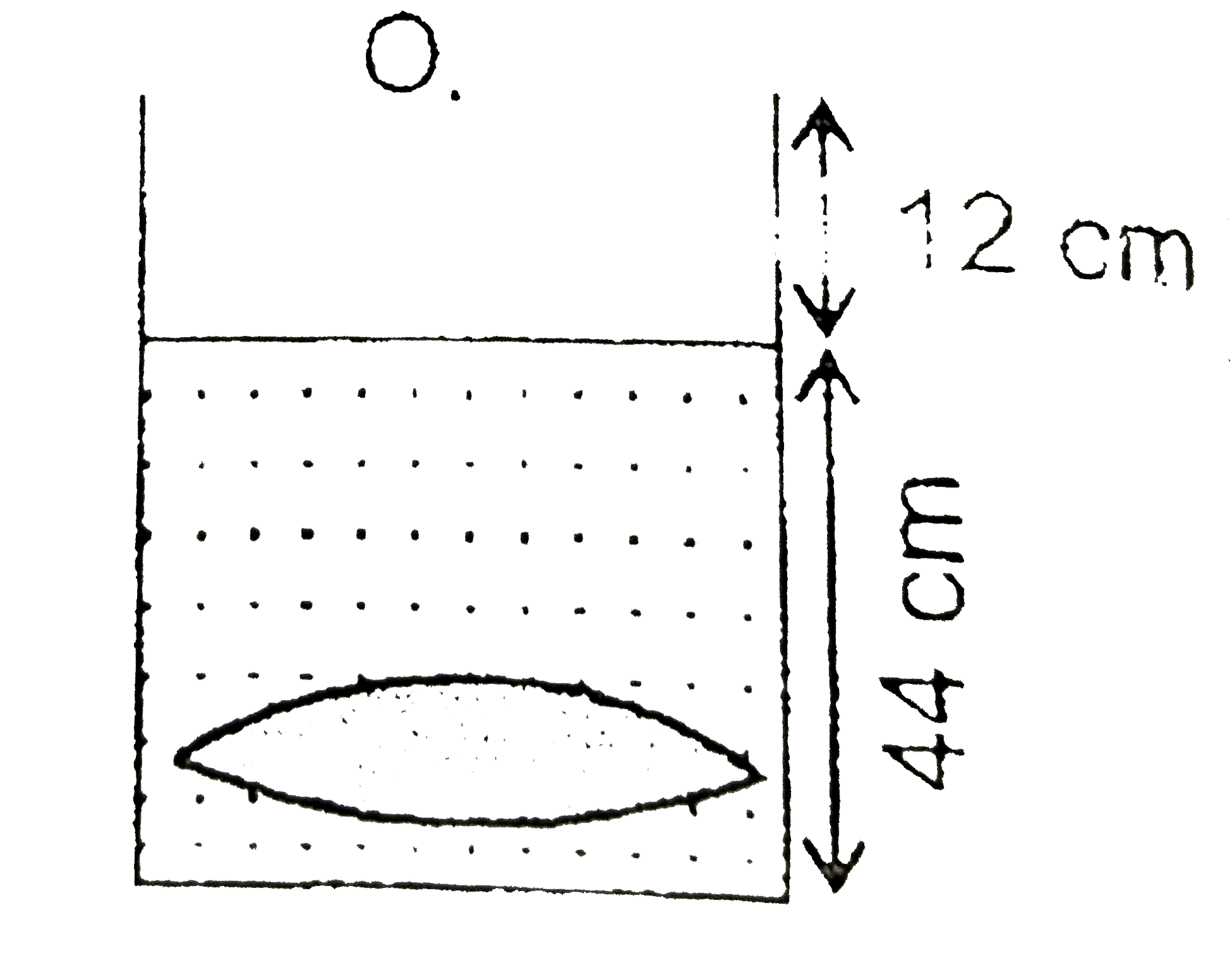
View Solution
Knowledge Check
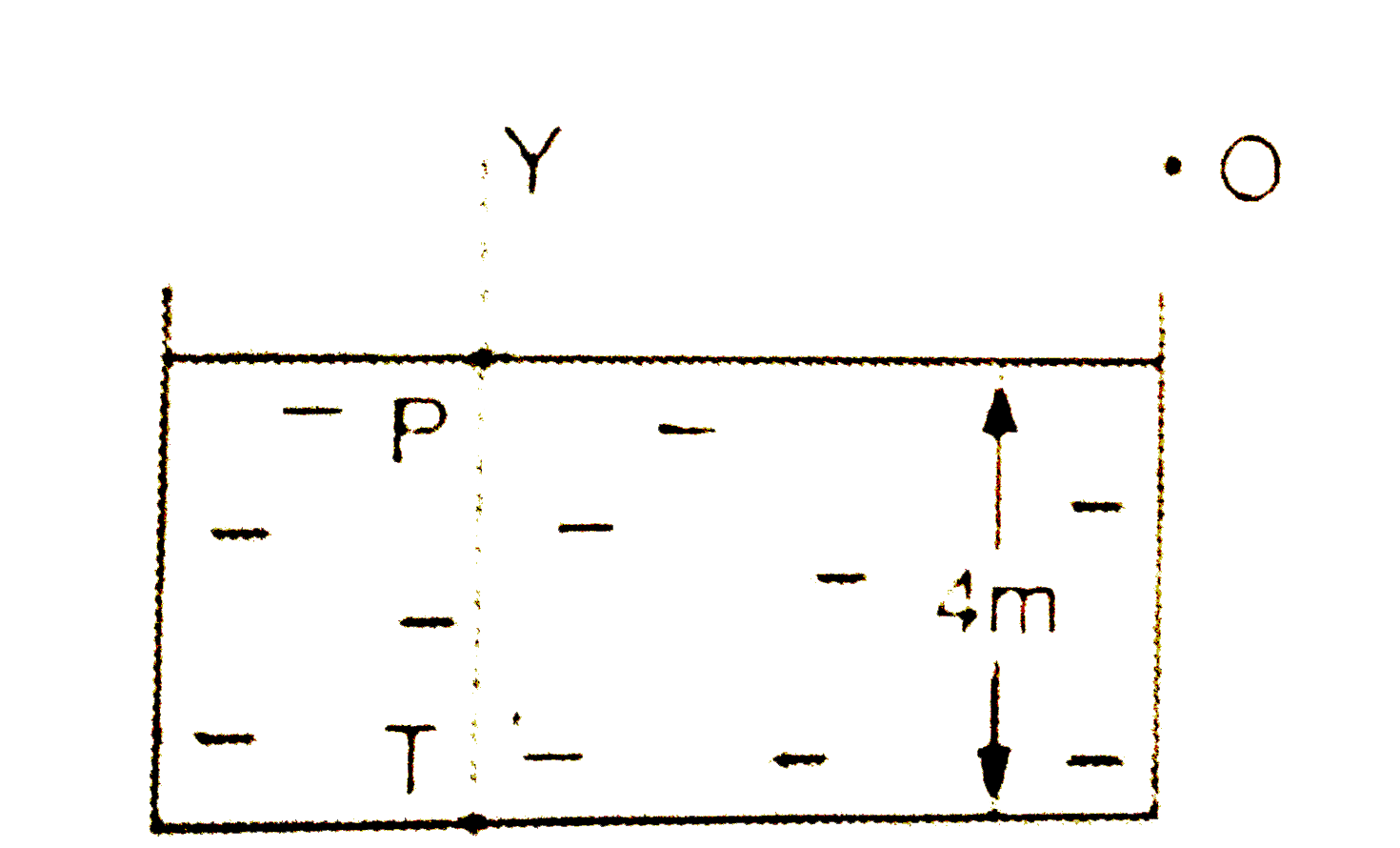
T is a point at the bottom of a tank filled with water, as shwon. The refractive index of water is 4/3. YPT is the vertical line through T. To an observer at the position O,T will appear to beAto the left of YTBsomewhere on YTCat a depth 3m below TDat a depth <3m below TThe time taken by the sunlight to reach the bottom of a tank of depth 4.5 m filled completely with water is …………. Ns. The refractive index of water is 43.
A2B20C1.5D200A point luminous object (O) is at a distance h from front face of a glass slab of width d and of refractive index μ. On the back face of slab is a refracting plane mirror. An observer sees the image of object in mirror as shown in figure. Distance of image from front face as seen by observer will be
 Ah+2dμB2h+2dCh+dDh+dμ
Ah+2dμB2h+2dCh+dDh+dμ
An object O is kept in air and a lens of focal length 10cm (in air) is kept at the botton of a container which is filled upto a height 44cm by water. The refractive index of water is 4/3 and that of glass is 3/2. The botton of the container is closed by a thin glass slab of refractive index 3/2. Find the distance (in cm) of the final image formed by the system from botton of container (refer to figure shown below).

View SolutionA coin is placed at the bottom of a beaker containing water (refractive index=4/3) at a depth of 12cm. By what height the coin appears to be raised when seen from vertical above ?
View SolutionA rectangular tank 8m deep is full of water. By how much does the bottom appear to be raised if the refractive index of water is 4/3?
View SolutionA plane mirror is fixed at the bottom of a tank containing water. A small object is kept at a height of 24 cm from the bottom and is viewed from a point vertically above it. The distance between the object and the image in the mirror as appears to the person is
View SolutionA coin is placed at the bottom of a glass trough containing water (refractive index = 43 ) up to a height 20 cm. At what depth it will appear when it is viewed from air, vertically above the coin. Draw a suitable ray diagram in support of your answer.
View Solution
