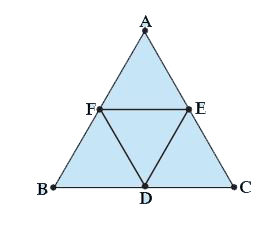
D, E और F क्रमशः त्रिभुज ABC की भुजाओं BC, CA और AB के मध्य बिन्दु हैं। दर्शाइए कि
(i) BDEF एक समांतर चतुर्भुज हैं।
(ii)ar(DEF)=14ar(ABC)
(iii)ar(BDEF)=12ar(ABC)
Step by step video & image solution for D, E और F क्रमशः त्रिभुज ABC की भुजाओं BC, CA और AB के मध्य बिन्दु हैं। दर्शाइए कि (i) BDEF एक समांतर चतुर्भुज हैं। (ii)ar(DEF)=1/4ar(ABC) (iii)ar(BDEF)=1/2ar(ABC) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- समांतर चतुभुजों और त्रिभुजों के क्षेत्रफल BOOK - SCIENCE PUBLICATIONCHAPTER - समांतर चतुभुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9.3 पर आधारित अभ्यास प्रश्न
8 Videos
- समांतर चतुभुजों और त्रिभुजों के क्षेत्रफल BOOK - SCIENCE PUBLICATIONCHAPTER - समांतर चतुभुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9.2 पर आधारित अभ्यास प्रश्न
6 Videos
- वृत्त BOOK - SCIENCE PUBLICATIONCHAPTER - वृत्त EXERCISE - प्रश्नावली 10.5 (पर आधारित अभ्यास प्रश्न )
10 Videos
- सांख्यिकीBOOK - SCIENCE PUBLICATIONCHAPTER - सांख्यिकीEXERCISE - प्रश्नावली 14.4 पर आधारित अभ्यास प्रश्न
10 Videos
Similar Questions
चित्र में यदि AD||BC है, तो सिद्ध कीजिए कि -
ar(COD)=ar(ABO)

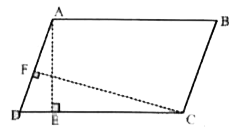
View Solutionचित्र में ABCD एक समान्तर चतुर्भुज हैं। AE ⊥DC तथा CF ⊥AD यदि AD = 6cm, CF = 10 cm और AE = 8 cm तो AB का मान ज्ञात कीजिए।
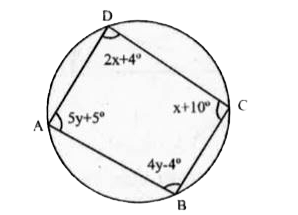
View Solutionआकृति में ABCD एक चक्रीय चतुर्भुज है। और y ज्ञात कीजिए
View Solution5 संख्याओं का माध्य 18 है। यदि एक संख्या हटा दी जाये तो, उनका माध्य 16 हो जाता है। हटायी गयी संख्या ज्ञात कीजिए।
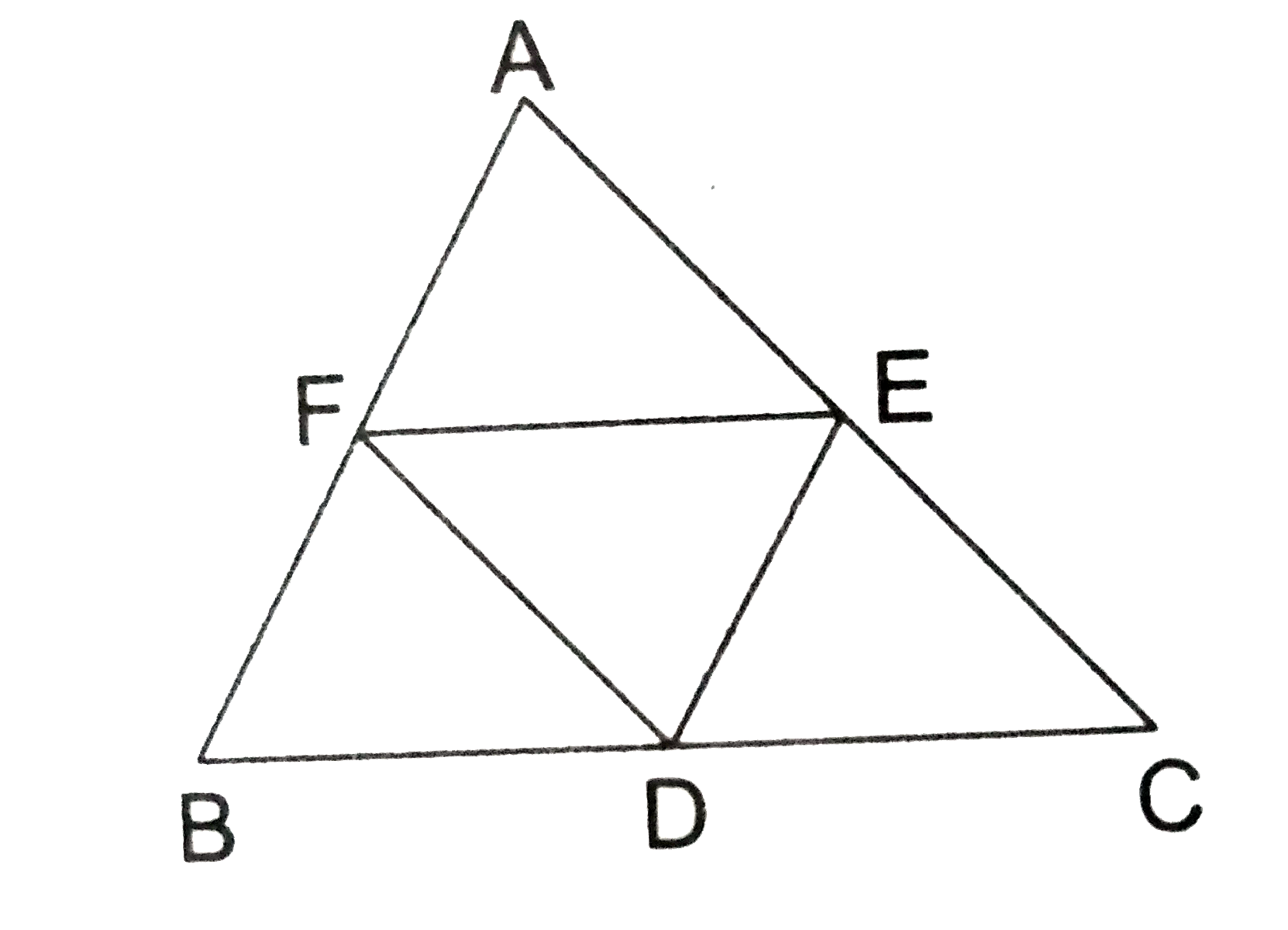
View SolutionD, E, F are the midpoints of the sides BC, CA and AB respectively of △ABC. Prove that
(i) BDEF is a ||gm,
(ii) ar(△DEF)=14ar(△ABC)and
(iii) ar(||gm BDEF)=12ar(△ABC)
View Solutionत्रिभुज ABC की भुजाओं BC , CA तथा AB के मध्य-बिंदु क्रमशा D , E तथा F है। सिद्ध कीजिए कि BDEF एक समांतर चतुर्भुज है जिसका क्षेत्रफल ΔABC का आधा है। साथ ही, सिद्ध कीजिए कि ar(ΔDEF)=14ar(ΔABC) तथा ar(।।gmBDEF)=12ar(ΔABC)
View Solutionदिए गए आकृति में ABC और BDF दो समबाहु त्रिभुज इस प्रकार है की D भुजा BC का मध्य बिंदु है |यदि AE भुजा BC को F पर प्रतिच्छेद करती है तो दर्शाई की
ar(BDF)=14ar(ABC)
(ii) ar(BDE)=12ar(BAE) ltBrgt (iii) ar(ABC)=2ar(BEC)
(iv) ar(BEF)=ar(AFD) ltBrgt (v) ar(BEF)=2ar(FED)
(vi)ar(FED)=18ar(AFC)
View SolutionP और Q क्रमशः त्रिभुज ABC की भुजाओं AB और BC के मध्य बिंदु है तथा R रेखाखण्ड AP का मध्य बिंदु है |दर्शाइए
(i)ar(PQR)=12ar(ARC)
(ii)ar(RQC)=38ar(ABC)
View Solutionयदि दो त्रिभुज ABC और DEF इस प्रकार है कि ABDE=BCEF=CAFD=25 तो ar(ΔABC):ar(ΔDEF)=
View SolutionD, E और F क्रमशः त्रिभुज ABC की भुजाओं BC, CA और AB के मध्य-बिन्दु है। दर्शाइए कि :
(i) BDEF का समान्तर चतुर्भुज है।
(ii) ar(DEF)=14ar(ABC)
(iii) ar(BDEF)=12ar(ABC)
View SolutionD, E तथा F, ΔABC कि क्रमश : भुजाओ BC, CA तथा AB के मध्यबिंदु है। सिद्ध कीजिए कि BDEF एक समांतर चतुर्भुज है तथा इसका क्षेत्रफल ΔABC के क्षेत्रफल का आधा है।
यह भी दिखाइए कि ar(DEF)=14ar(ABC).
View Solutionसत्य/असत्य बताइए तथा उत्तर का औचित्य भी बताइए -
ABC और BDE दो समबाहु त्रिभुज इस प्रकार है की D भुजा BC का मध्य-बिंदु है। तब
ar(BDE)=14ar(ABC).
View SolutionD,E and F are respectively the mid-points of the sides BC, CA and AB of △ABC show that
(i) BDEF is a parallelogram.
(ii) ar (DEF) = 14 ar (ABC)
(iii) ar(BDEF)=12 ar (ABC)
View SolutionIn the following figure , ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, show that
(i) ar (BDE) = 14 ar (ABC)
(ii) ar (BDE) = 12 ar (BAE)
(iii) ar (ABC)= 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = 18 ar(AFC)
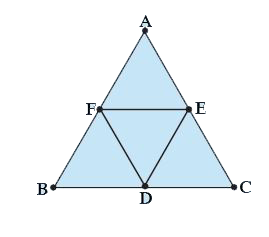
View SolutionIn the figure, ΔABC, D, E, F are the midpoints of sides BC, CA and AB respectively. Show that
(i) BDEF is a parallelogram
(ii) ar(ΔDEF)=14ar(ΔABC)
(iii) ar(BDEF)=12ar(ΔABC)
View SolutionIn the figure, ΔABC, D, E, F are the midpoints of sides BC, CA and AB respectively. Show that
(i) BDEF is a parallelogram
(ii) ar(ΔDEF)=14ar(ΔABC)
(iii) ar(BDEF)=12ar(ΔABC)
View Solution
