आकृति में, ABC और ABD एक ही आधार AB पर बने दो त्रिभुज हैं। यदि रेखाखंड CD रेखाखंड AB से बिन्दु O पर समद्विभाजित होता है, तो दर्शाइए कि ar(ABC) = ar(ABD) है।
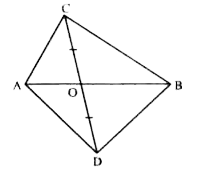
Step by step video & image solution for आकृति में, ABC और ABD एक ही आधार AB पर बने दो त्रिभुज हैं। यदि रेखाखंड CD रेखाखंड AB से बिन्दु O पर समद्विभाजित होता है, तो दर्शाइए कि ar(ABC) = ar(ABD) है। by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- समांतर चतुभुजों और त्रिभुजों के क्षेत्रफल BOOK - SCIENCE PUBLICATIONCHAPTER - समांतर चतुभुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9.3 पर आधारित अभ्यास प्रश्न
8 Videos
- समांतर चतुभुजों और त्रिभुजों के क्षेत्रफल BOOK - SCIENCE PUBLICATIONCHAPTER - समांतर चतुभुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9.2 पर आधारित अभ्यास प्रश्न
6 Videos
- वृत्त BOOK - SCIENCE PUBLICATIONCHAPTER - वृत्त EXERCISE - प्रश्नावली 10.5 (पर आधारित अभ्यास प्रश्न )
10 Videos
- सांख्यिकीBOOK - SCIENCE PUBLICATIONCHAPTER - सांख्यिकीEXERCISE - प्रश्नावली 14.4 पर आधारित अभ्यास प्रश्न
10 Videos
Similar Questions
चित्र में यदि AD||BC है, तो सिद्ध कीजिए कि -
ar(COD)=ar(ABO)

View Solutionचित्र में ABCD एक समान्तर चतुर्भुज हैं। AE ⊥DC तथा CF ⊥AD यदि AD = 6cm, CF = 10 cm और AE = 8 cm तो AB का मान ज्ञात कीजिए।
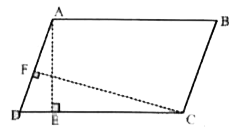
View Solutionआकृति में ABCD एक चक्रीय चतुर्भुज है। और y ज्ञात कीजिए
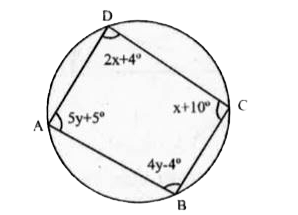
View Solution5 संख्याओं का माध्य 18 है। यदि एक संख्या हटा दी जाये तो, उनका माध्य 16 हो जाता है। हटायी गयी संख्या ज्ञात कीजिए।
View SolutionIn the given figure (not to scale), O is the centre of the circle. A,B,C and D are concyclic and AB=CD . If /_MON =120^(@) , then find /_ OPN .
View Solution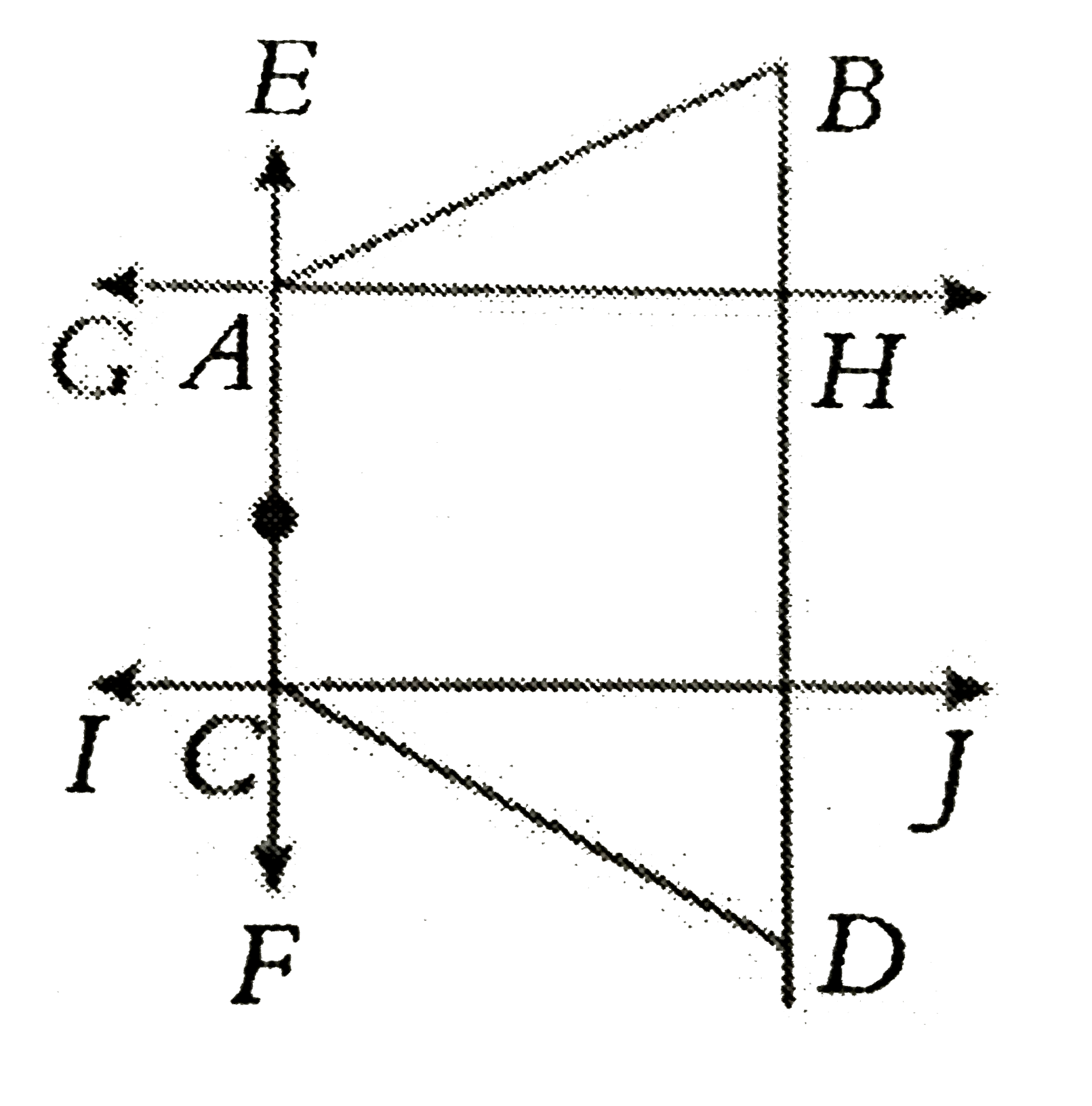
In the above figure, GH∣∣IJ and AC∣∣BD,AB and CD are bisectors of ∠EAH and ∠FCJ respectively. Find the ∠ABD+∠BDC, if ∠BAC=3∠BDC.
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionIn the figure above (not to scale), ¯¯¯¯¯¯AB⊥¯¯¯¯¯¯CDandAD is the bisector of ∠BAE.AB=3cm and AC=5cm. Find CD.
View SolutionIn the following figure, AB and BC are equidistant from the centre 'O' of the Show that
(a) ABC is an isosceles triangle.
(b) OB bisects angle ABC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_X_C13_E02_006_Q01.png" width="80%"gt
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionIn the figure (not to scale) AB = AC and BD = CD. Find ∠ADB
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C15_E05_003_Q01.png" width="80%"gt
View Solution
