यदि परस्पर लम्बवत दो ऊर्ध्वाधर तलों में नति कोण, $δ_{1}$ और $δ_{2}$ दिखें और वास्तविक नति कोण $δ$ हो, तो सिद्ध करें कि ${cot}^{2} δ = {cot}^{2} δ_{1} + {cot}^{2} δ_{2}$

Video Solution

Text Solution

Verified by Experts

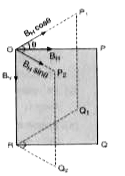
मान लें कि स्थान O पर OPOR, चुम्बकीय याम्योत्तर दर्शाता है जहाँ OP, पृथ्वी के चुम्बकीय क्षेत्र का क्षैतिज घटक $B_{H}$ दर्शाता है। फिर $O P_{1} Q_{1} R$ और पर $O P_{2} O_{2} R$ कोई दो परस्पर लम्बवत तल | दर्शाते हैं जिस प्रकार चित्र 8.29 में $B_{V}$ दर्शाया गया है। यदि OPQR और $O P_{1} O_{1} R$ के बीच कोण $θ$ हो, तो $O P_{1}$ दिशा में $B_{H}$ का घटक $B_{H_{I}}$ है और $O P_{2}$ दिशा में $B_{H_{2}}$ जहाँ $B H_{1} = B_{H} = cos θ$ और $B_{H_{2}} = B_{H} = sin θ$ यहाँ O पर नति कोण का वास्तविक मान $= δ$ तल $O P_{1} Q_{1} R$ में O पर नति कोण का आभासी मान $= δ$ तल $O P_{2} Q_{2} R$ में O पर नति कोण का आभासी मान $= δ$ और स्थान O पर पृथ्वी के चुम्बकीय क्षेत्र का ऊर्ध्वाधर घटक $= B_{V}$ स्पष्टतया
$tan δ = \frac{B_{V}}{B_{H}} ... . (i)$
${tan δ}_{1} = \frac{B_{V}}{B_{H_{1}}} = \frac{B_{V}}{B_{H} cos θ} ... (i i)$
और ${tan δ}_{2} = \frac{B_{V}}{B_{H_{2}}} = \frac{B_{V}}{B_{H} sin θ} ... . . (i i i)$
समीकरण (i), (ii) और (iii) से
$cot δ = \frac{B_{H}}{B_{V}} ... (i v)$
${cot δ}_{1} = \frac{B_{H} cos θ}{B_{V}} ... (v)$
और ${cot δ}_{2} = \frac{B_{H} sin θ}{B_{V}} ... (v i)$
समीकरण (v) और (vi) का वर्ग करके जोड़ने पर हम पाते हैं
${cot}^{2} δ_{1} + {cot}^{2} δ_{2} = \frac{B_{H}^{2} {cos}^{2} θ}{B_{V}^{2}} + \frac{B_{H}^{2} {sin}^{2} θ}{B_{V}^{2}}$
$= \frac{B_{H}^{2}}{B_{V}^{2}} ({cos}^{2} θ + {sin}^{2} θ)$
$= \frac{B_{H}^{2}}{B_{V}^{2}} {cot}^{2} δ$ [ समीकरण (iv) से]
इस प्रकार ${cot}^{2} δ = {cot}^{2} δ_{1} + {cot}^{2} δ_{2}$

Updated on:21/07/2023

|

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

GRB PUBLICATION HINDI-चुम्बकत्व-विषय-आधारित समस्याएँ : हल सहित

Home
Ask Doubt
Profile