$\frac{1}{f} = (μ - 1) \frac{1}{r_{1}} - \frac{1}{r_{2}}$ सूत्र का स्थापित करें।

Video Solution

Text Solution

Verified by Experts

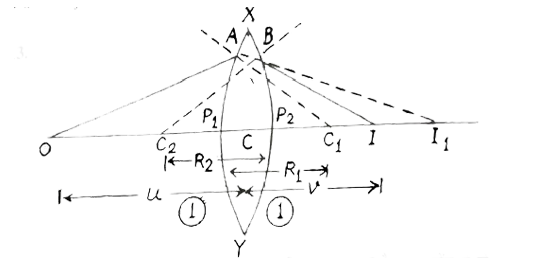
माना XY एक लेंस है तथा इसके मुख्य अक्ष पर एक विन्दुवत वस्तु O है। इस लेंस में दो सतह $X P_{1} Y$ तथा $X P_{2} Y$ है।
अब सतह $X P_{1} Y$ से अपवर्तन- यहाँ अपवर्तन विरल माध्यम से सघन माध्यम में हो रहा है।
अंत: $\frac{- n_{1}}{P_{1} O} + \frac{n_{2}}{P_{1} l_{1}} = \frac{n_{2} - n_{1}}{P_{1} C_{1}}$ ...(i)
अब सतह $X P_{2} Y$ से अपवर्तन- अब यह स्थिति है कि वस्तु सघन माध्यम में स्थित है और प्रतिबिम्ब विरल माध्यम में बना रहा है।
अंत $\frac{- n_{2}}{P_{2} l_{1}} + \frac{n_{1}}{P_{2} l} = \frac{n_{1} - n_{2}}{P_{2} C_{2}} = \frac{(n_{2} - n_{1})}{P_{2} C_{2}}$ ...(ii)
समी (i) और (ii) को जोड़ने पर हम पाते है
$\frac{- n_{1}}{P_{1} O} + \frac{n_{2}}{P_{1} l_{1}} + \frac{- n_{2}}{P_{2} l_{1}} + \frac{n_{1}}{P_{2} l} = (n_{2} - n_{1}) [\frac{1}{P_{1} C_{1}} - \frac{1}{P_{2} C_{2}}]$
चूँकि लेंस बहुत पतला है अंत: बिंदु $P_{1}$ तथा $P_{2}$ बिंदु (से बहुत नजदीक है। )
अंत $P_{1}$ तथा $P_{2}$ की जगह हम C लिख सकते है, तो समी (iii) निम्न रूप में हो जाएगा।
$\frac{- n_{1}}{C O} + \frac{n_{1}}{C l} = (n_{2} - n_{1}) (\frac{1}{R_{1}} - \frac{1}{R_{2}})$
चिह्र पढ़ती लगने पर $C O = - u$ , तथा $C l = + V$
अंत $\frac{- n_{1}}{u} + \frac{n_{1}}{V} = (n_{2} - n_{1}) [\frac{1}{R_{1}} - \frac{1}{R_{2}}]$
या $\frac{1}{u} + \frac{1}{V} = [\frac{n_{2}}{n_{1}} - 1] [\frac{1}{R_{1}} - \frac{1}{R_{2}}]$
परन्तु $\frac{n_{2}}{n_{1}} = n$ विरल माध्यम के सापेक्ष सघन माध्यम का अपवर्तनांक
$∴ \frac{1}{u} + \frac{1}{V} = (n - 1) [\frac{1}{R_{1}} - \frac{1}{R_{2}}]$
यदि वस्तु अनंत पर है, तो प्रतिबिम्ब, लेंस के मुख्य फोकस पर बनता है अर्थात यदि $u = \infty$ तथा V=f अंत: smi (iv) निम्न रूप में होगी :
$\frac{1}{\infty} + \frac{1}{f} = (n - 1) [\frac{1}{R_{1}} - \frac{1}{R_{2}}]$
या $\frac{1}{f} = (n - 1) [\frac{1}{R_{1}} - \frac{1}{R_{2}}] (∴ \frac{1}{\infty} = 0)$ यह फर्मूला सत्यापित हुआ।

|

Updated on:21/07/2023

Class 12 PHYSICS PHYSICAL WORLD

Topper's Solved these Questions

Similar Questions

BIHAR BOARD- PREVIOUS YEAR PAPER-भौतिक विज्ञान 2012-खंड-II (गैर-वस्तुनिष्ठ)

Home
Ask Doubt
Profile