व्यतिकरण का परिभाषित करें। यंग के द्विक छिद्र प्रयोग में फ्रिंज की चौड़ाई का व्यंजक ज्ञात करें।

Video Solution

Text Solution

Verified by Experts

व्यक्तिकरण-दो कला सम्बद्ध स्रोतों से निकली प्रकाश तरंगो के व्यक्तिकरण के कारण प्रकाश ऊर्जा का पुनर्वितरण ही व्यक्तिकरण कहलाता है। यंग ने प्रकाश में व्यतिकरण की घटना को दिखाया। उसने सूर्य प्रकाश को बारीक़ स्लिट S (पिन-छिद्र) के बराबर गिरने दिया, जैसा कि निचे चित्र में दिखाया गया है।

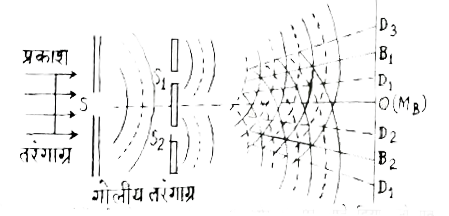
स्लिट (S) से प्रकाश तरंगो की दो बारीक़ स्लिट $S_{1}$ और $S_{2}$ पर जाने दिया, तो एक दूसरे निकट तथा समांतर थी। $S_{1}$ और $S_{2}$ ,S से समान दुरी पर थी। ये स्लिट $S_{1}$ तथा $S_{2}$ समान आयाम और समान तरंगदैर्ध्य की तरंगे देती है। इन तरंगो को एक दूसरे पर अध्यारोपित किया गया और व्यक्तिकरण कराया गया और उन्होंने पर्दे पर काले और चमकीले बैंड प्राप्त किये। ऊपर चित्र में काले बैंड D से प्रदर्शित किया गए है, जबकि चमकीले बैंड .B. से प्रदर्शित किये गए है । फ्रिंज चौड़ाई का व्यंजक : फ्रिंज चौड़ाई- दो क्रमागत दीप्त अथवा अदीप्त फ़्रिजो की मध्य दुरी फ्रिंज चौड़ाई कहलाती है।

माना $S_{1}$ तथा $S_{2}$ के बीच की दुरी d है तथा दोनों स्रोतों के पृष्ठ से पर्दा की दुरी D है। चूँकि $S_{1}$ और $S_{2}$ से निकली प्रकाश की किरण पर्दे पर O बिंदु पर समान दुरी तय करके पहुंचती है । अंत: इन दोनों का पथांतर और कलांतर शून्य है । अंत बिंदु O पर चमकीली फ्रिंज प्राप्त होते है। चित्र से, किरण $S_{1} P$ तथा $S_{2} P$ के बीच पथांतर होगा
$Δ x = S_{2} P - S_{1} P$
समकोण त्रिभुज $Δ S_{2} P B$ में $S_{2} P = {(S_{2} B^{2} + P B^{2})}_{2}^{1 / 2}$
या $S_{2} P = {[D^{2} + {(y + \frac{d}{2})}^{2}]}^{1 / 2} = D {⎡ ⎢ ⎢ ⎢ ⎣ 1 + \frac{{(y + \frac{d}{2})}^{2}}{D^{2}} ⎤ ⎥ ⎥ ⎥ ⎦}^{1 / 2}$
द्विपद प्रमेय के प्रयोग से, उच्च घात वाले पदों का नगण्य मानकर
$S_{2} P = D ⎡ ⎢ ⎢ ⎢ ⎣ 1 + \frac{{(y + \frac{d}{2})}^{2}}{2 D^{2}} ⎤ ⎥ ⎥ ⎥ ⎦ ∴ S_{2} P = D + \frac{{(y + \frac{d}{2})}^{2}}{2 D}$ ...(ii)
इसी प्रकार समकोण त्रिभुज $Δ S_{1} A P$ से $S_{1} P = D + \frac{{(y - \frac{d}{2})}^{2}}{2 D}$ ...(iii)
समी (ii) और (iii) से मान (i) में रखने पर
$Δ x = D + \frac{{(y + \frac{d}{2})}^{2}}{2 D} - D - \frac{{(y - \frac{d}{2})}^{2}}{2 D}$
या $Δ x = \frac{{(y + \frac{d}{2})}^{2}}{2 D} - \frac{{(y - \frac{d}{2})}^{2}}{2 D}$ या $Δ x = \frac{{(y + \frac{d}{2})}^{2} - {(y - \frac{d}{2})}^{2}}{2 D}$
या $Δ x = \frac{[y + \frac{d}{2} + y - \frac{d}{2}] [v + \frac{d}{2} - \frac{y_{d}}{2}]}{2 D}$
$Δ x = \frac{2 y d}{2 D} = \frac{y d}{D} Δ x = \frac{y d}{D}$
(दीप्त फ्रिंज- अगर पथांतर $λ$ का समगंज है तब दीप्त फ्रिज का निर्माण होगा । अर्थात P पर दीप्त फ्रिज बनेगी।
अंत $\frac{y d}{D} = m λ$ या $y = \frac{m λ D}{d}$
जो m वीं दीप्त फ्रिज की केंद्रीय दीप्त फ्रिज से स्थिति है। यदि $m = 1, y_{1} = \frac{λ D}{d}$ , केंद्रीय दीप्त फ्रिंज से प्रथम दीप्त फ्रिंज की स्थिति यदि $m = 2, y_{2} = \frac{2 λ D}{d}$ , केंद्रीय दीप्त फ्रिंज से द्वितीय दीप्त फ्रिज की स्थिति यदि $m = (m - 1), y_{m - 1} = \frac{(m - 1) λ D}{d}$
जो $(m - 1)$ वीं दीप्त फ्रिज की केंद्रीय दीप्त फ्रिज से स्थिति है। दीप्त फ्रिंज चौड़ाई $(β)$ -
अर्थात $β = y_{2} - y_{1} = \frac{2 λ D}{d} - \frac{λ D}{d}$
अथवा $β = y_{2} = y_{1} = \frac{2 λ D}{d} - \frac{λ D}{d}$ अथवा $β = \frac{λ D}{d}$
अदीप्त फ्रिजे -यदि पथांतर $λ / 2$ का विषम गुणज हो तब P पर अदीप्त फ्रिज बनती है। अर्थात $\frac{y d}{D} = (2 n + 1) \frac{λ}{2}$ जहाँ n=1,2,3
या $y = \frac{(2 m + 1) λ D}{2 d}$
जो m वां अदीप्त फ्रिज को केंद्रीय फ्रिज से स्थिति है।
यदि $m = 0, y_{0} = \frac{λ D}{2 d}$ , प्रथम अदीप्त फ्रिंज की केंद्रीय दीप्त फ्रिंज से स्थिति
यदि $m = 0.1, y_{1} = \frac{3 λ D}{2 d}$ , द्वितीय अदीप्त फ्रिंज की केंद्रीय दीप्त फ्रिंज से स्थिति
यदि $m = (m - 1), y_{(m - 1)} = \frac{(2 m + 1) λ D}{2 d}, (m - 1)$
अदीप्त फ्रिंज की केंद्रीय दीप्त फ्रिंज स्थिति।
अदीप्त फ्रिंज चौड़ाई $(β)$ = दो क्रमागत अदीप्त फ्रिज से के मध्य की दुरी फ्रिंज चौड़ाई कहलाता है।
अर्थात $β = y_{1} - y_{0} = \frac{3 λ D}{2 d} - \frac{λ D}{2 d}$ अथवा $β = \frac{λ D}{2 d}$

|

Updated on:21/07/2023

Class 12 PHYSICS PHYSICAL WORLD

Topper's Solved these Questions

Similar Questions

BIHAR BOARD- PREVIOUS YEAR PAPER-भौतिक विज्ञान 2012-खंड-II (गैर-वस्तुनिष्ठ)

Home
Ask Doubt
Profile