A cube of side 'b' has a charge 'q' at each of its vertices. Determine

A cube of side x has a charge q at each of its vertices. Determine the potential due to this charge array at the center of the cube.
A $\frac{4 q}{3 π ε_{0} x}$
B $\frac{4 q}{\sqrt{3} π ε_{0} x}$
C $\frac{3 q}{4 π ε_{0} x}$
D $\frac{2 q}{\sqrt{3} π ε_{0} x}$
A hexagon of side 'a' has a charge 'q' at each of its vertices. The electric field at the centre of hexagon is
A $0$
B $\frac{1}{4 π \in_{0}} . \frac{q}{a^{2}}$
C $\frac{1}{4 π \in_{0}} . \frac{6 q}{a^{2}}$
D $\frac{1}{4 π \in_{0}} . \frac{6 q^{2}}{a^{2}}$
A cube of side 'a' has point charges +Q located at each of its vertices except at the origin where the charge is -Q. The electric field at the centre of cube is :

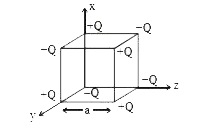A $\frac{- Q}{3 \sqrt{3} π ε_{0} a^{2}} (ˆ x + ˆ y + ˆ z)$
B $\frac{- 2 Q}{3 \sqrt{3} π ε_{0} a^{2}} (ˆ x + ˆ y + ˆ z)$
C $\frac{2 Q}{3 \sqrt{3} π ε_{0} a^{2}} (ˆ x + ˆ y + ˆ z)$
D $\frac{Q}{3 \sqrt{3} π ε_{0} a^{2}} (ˆ x + ˆ y + ˆ z)$

A cube of side 'b' has a charge 'q' at each of its vertices. Determine the potential and electric field due to this charge array at the centre of the cube.