Let S be a square of nit area. Consider any quadrilateral, which has none vertex on each side of S. If a,b,candd denote the lengths of the sides of het quadrilateral, prove that 2≤a2+b2+c2+x2≤4.
Let the squares S is to be bounded by the lines x=±1/2andy=±1/2
We have, a2=(x1−12)2+(12−y1)2
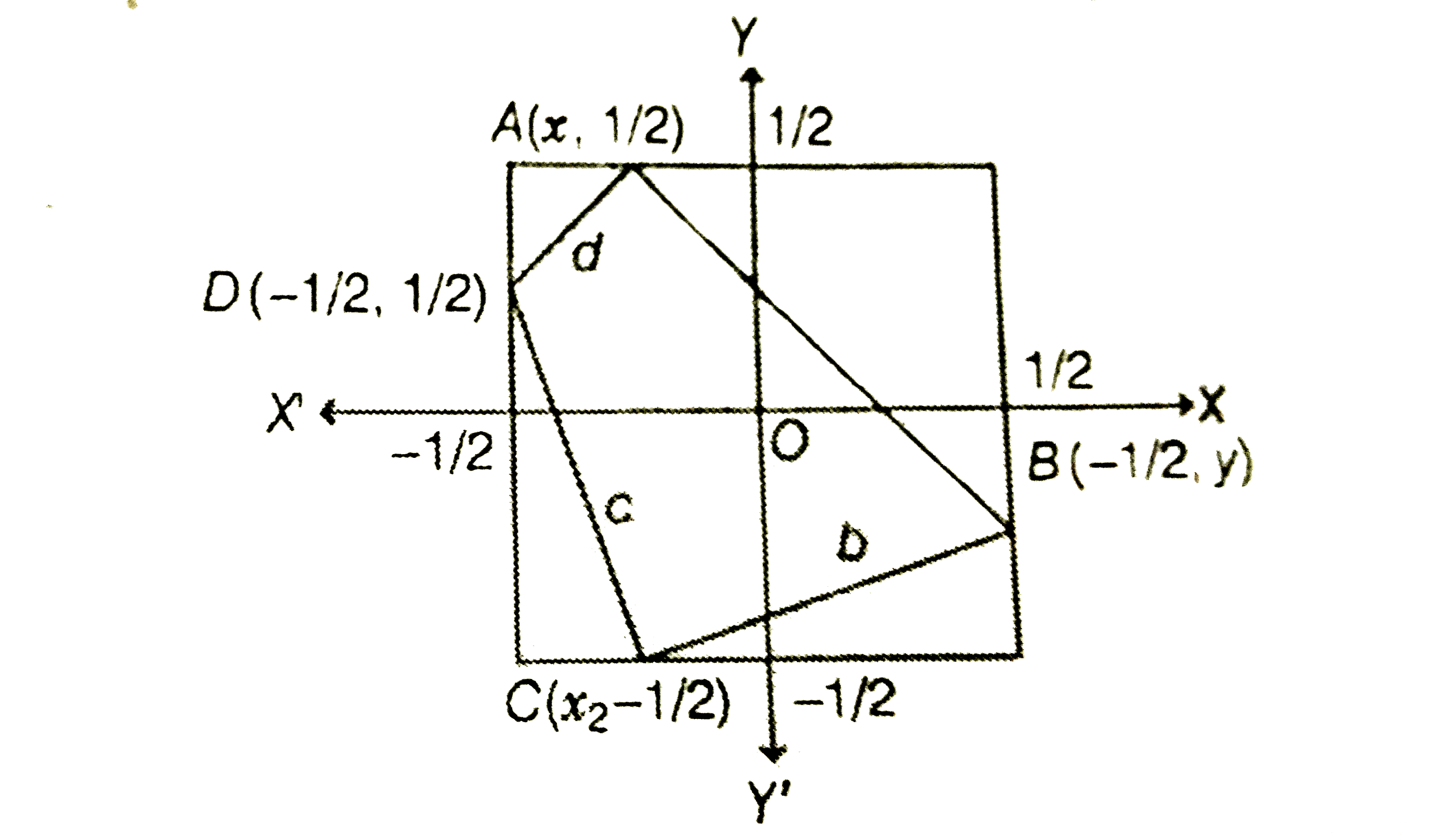
=x21−y21−x1−y1+12
Similarly, b2=x22−y21−x2+y1+12
c2=x22−y22+x2+y2+12
d2=x21−y22+x1−y2+12
∴a2+b2+c2+d2=2(x21+y21+x22+y22)+2
Therefore, 0≤x21,x22,y21,y22≤14
0≤x21+x22+y21+y22≤1
⇒ 0≤2(x21+x22+y21+y22)≤2
But 2≤2(x21+x22+y21+y22)+2≤4
Alternate solution
c2=x22+y22 ... (i)
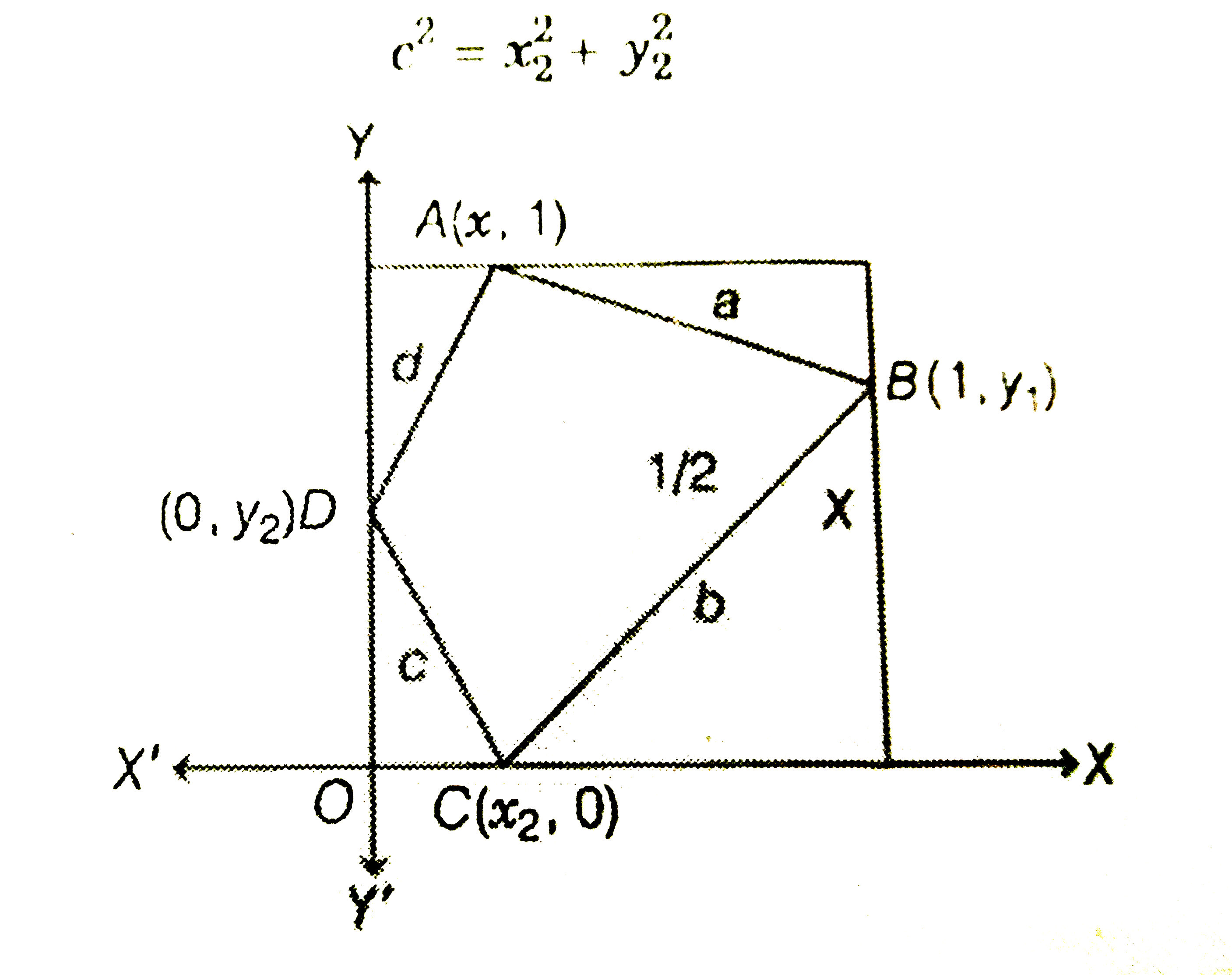
b2=(1−x2)2+y21 ... (ii)
a2=(1−y1)2+(1−x1)2 ... (iii)
d2=x21+(1−y2)2 ... (iv)
On adding Eqs. (i), (ii), (iii) and (iv), we get
a2+b2+c2+d2={x21+(1−x1)2}+{y21+(1−y1)2}+{x22+(1−x2)2}+{y22+(1−y2)2}
where x1,y1,x2,y2 all vary in the interval [0,1]
Now, consider the function y=x2+(1−x2),0≤x≤1
differentiating ⇒dydx=2x−2(1−x). For maximum or minimum dydx=0.
⇒2x−2(1−x)=0⇒2x−2+2x=0
⇒4x=2 ⇒x=1/2
Again, d2ydx2=2+2=4
Hence, y is minimum at x=12 and its minimum value is 1/4. Clearly, value is maximum when x=1.
∴ Minimum value of a2+b2+c2+d2=12+12+12+12=2
and maximum value is 1+1+1+1=4
Topper's Solved these Questions
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - MAXIMA AND MINIMA ( INTEGER ANSWER TYPE QUESTIONS)8videos
APPLICATION OF DERIVATIVES
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - MAXIMA AND MINIMA (PASSAGE BASED PROBLEMS)3videos
APPLICATION OF DERIVATIVES
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - 3D GeometryEXERCISE - Equation of Plane Objective Question II (Integer Answer Type Question)1videos
3D Geometry
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - AREAEXERCISE - AREA USING INTEGRATION55videos
AREA
Similar Questions
Let S be a square of nit area. Consider any quadrilateral, which has none vertex on each side of S. If a,b,candd denote the lengths of the sides of het quadrilateral, prove that 2≤a2+b2+c2+x2≤4.
View SolutionLet S be a square of unit area. Consider any quadrilateral which has one vertex on each side of S. If a,b,c and d denote the lenghts of the sides of the quadrilateral,
Prove that 2≤a2+b2+c2+d2≤4.View Solution
Knowledge Check
- Question 1 - Select One
A quadrilateral has one vertex on each side of a square of side-length 1. If the lengths of the quadrilateral are a, b, c, d, then
A2≤a2+b2+c2+d2≤4B1≤a2+b2+c2+d2≤4C√2≤a2+b2+c2+d2≤4D2√2≤a2+b2+c2+d2≤4 - Question 2 - Select One
Which of the following best describes the values of k, if a, b and c are the lengths of the sides of the triangle and k=a2+b2+c2ab+bc+ca ?
AA. 1≤k<2BB. 0≤k<2CC. 0<k<98DD. 1≤k≤2 - Question 3 - Select One
A quadrilateral has the vertices at the points (-4, 2), (2, 6), (8, 5) and (9, -7). Show that the mid-points of the sides of this quadrilateral are the vertices of a parallelogram
ARectangleBSquareCParallelogramDRhombus
Let S be the square of unit area. Consider any quadrilateral which has one vertex on each side of S. If a, b, c and d denote the lengths of the sides of the quadrilateral, prove that 2≤a2+b2+c2+d2≤4.
View SolutionIf a,b,c are the lengths of the sides of a triangle,then the range of ab+bc+caa2+b2+c2
View SolutionIf a,b,c,d are the side of a quadrilateral, then find the the minimuym value of a2+b2+c2d2
View SolutionA quadrilateral has the vertices at the points (−4,2), (2,6), (8,5) and (9,−7) . Show that the mid points of the sides of this quadrilateral are the vertices of a parallelogram.
View SolutionLet a≤b≤c be the lengths of the sides of a triangle. If a2+b2<c2, then prove that triangle is obtuse angled .
View Solution

