Let be the vertices of triangle ABC. A parallelogram AFDE is drawn with D,E, and F on the line segments BC, CA and AB, respectively. Using calculus, show that the maximum area of such a parallelogram is
Let are similar.
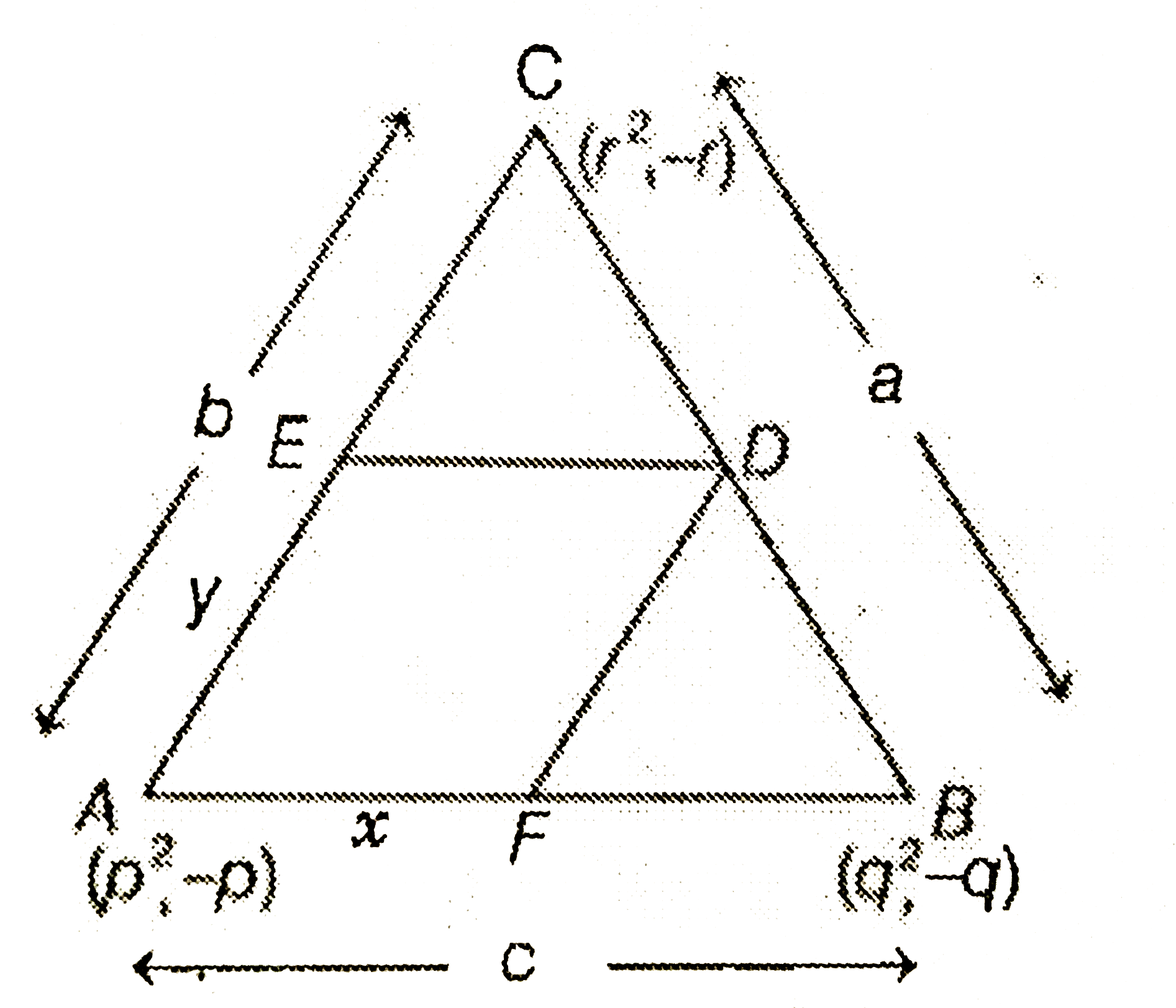
Let z denotes the area of par
allelogram AFDE.
Then,
... (i)
On differentiating w.r.t. y we get
For maximum or minimum values of z, we must have
Clearly,
Hence, z is maximum, when .
On putting in Eq. (i), we get
the maximum value of z is
area of
Applying
Topper's Solved these Questions
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - MAXIMA AND MINIMA ( INTEGER ANSWER TYPE QUESTIONS)8videos
APPLICATION OF DERIVATIVES
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - MAXIMA AND MINIMA (PASSAGE BASED PROBLEMS)3videos
APPLICATION OF DERIVATIVES
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - 3D GeometryEXERCISE - Equation of Plane Objective Question II (Integer Answer Type Question)1videos
3D Geometry
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - AREAEXERCISE - AREA USING INTEGRATION55videos
AREA
Similar Questions
Let A(1,−1),B(4,−2)andC(9,3) be the vertices of the △ABC. A parallelogram AFDE is drawn with vertices D, E and F on the line segments BC, CA and AB respectively Find the maximum area of parallelogram AFDE.
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
View Solution
Knowledge Check
- Question 1 - Select One
Let P be an interior point of a triangle ABC , Let Q and R be the reflections of P in AB and AC , respectively if Q .A , R are collinear then ∠A equals -
A30∘B60∘C90∘D120∘ - Question 2 - Select One
If G(3,−5,r) is centroid of triangle ABC where A(7,−8,1),B(p,q,5)andC(q+1,5p,0) are vertices of a triangle then values of p,q,r are respectively
A6,5,4B−4,5,4C−3,4,3D−2,3,2 - Question 3 - Select One
If G(3, -5, r) is centroid of triangle ABC where A(7, - 8, 1), B(p, q, 5) and C(q + 1, 5p, 0) are vertices of a triangle then values of p, q, r are respectively ...
A6,5,4B−4,5,4C−3,4,3D−2,3,2
If P(–2,4),Q(4,8),R(10,5)andS(4,1) are the vertices of a quadrilateral, show that it is a parallelogram.
View SolutionProve that the figure formed by joining the mid-points of the pair of consecutive sides of a quadrilateral is a parallelogram. OR BACD is a parallelogram in which P,Q,R and S are mid-points of the sides AB,BC,CD and DA respectively. AC is a diagonal. Show that : PQ∣∣AC and PQ=12AC SR∣∣AC and SR=12AC PQ=SR (iv) PQRS is a parallelogram.
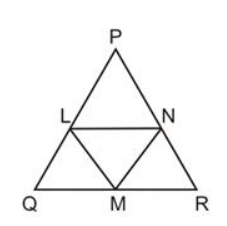
View SolutionIn ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.
 View Solution
View SolutionABCD is a parallelogram. P is the mid-point of AB.BD and CP intersect at Q such that CQ:QP=3:1. If ar (PBQ)=10 cm2, find the area of parallelogram ABCD
View SolutionThe sides AB,BC and AC of a triangle ABC touch a circle with centre O and radius r at P, Q, and R respectively.
View Solution

