For balmer series in the spectrum of atomic hydrogen the wave number of each line is given by ¯¯¯V=R[1n21−1n22] where RH is a constant and n1 and n2 are integers. Which of the following statements (s), is (are correct)
1. As wave length decreases the lines in the series converge
2. The integer n1 is equal to 2.
3. The ionisation energy of hydrogen can be calculated from the wave numbers of three lines.
4. The line of shortest wavelength corresponds to = 3.
1, 2 and 3
2 , 3 and 4
1,2 and 4
2 and 4 only
The correct Answer is:C
(1)Beyond a certain wavelength the line spectrum becomes band spectrum.
(2)For Balmer series n1=2
(4)The line of longest wavelength in this series , n2=3
Topper's Solved these Questions
- ATOMIC STRUCTUREBOOK - ERRORLESS CHAPTER - ATOMIC STRUCTUREEXERCISE - Dual nature of electron
28 Videos
- ATOMIC STRUCTUREBOOK - ERRORLESS CHAPTER - ATOMIC STRUCTUREEXERCISE - Uncertainty principle and Schrodinger wave equation
22 Videos
- ATOMIC STRUCTUREBOOK - ERRORLESS CHAPTER - ATOMIC STRUCTUREEXERCISE - Atomic number, Mass number, Atomic species
56 Videos
- SURFACE CHEMISTRYBOOK - ERRORLESS CHAPTER - SURFACE CHEMISTRYEXERCISE - JEE Section (Matching Column)
2 Videos
Similar Questions
Knowledge Check
For balmer series in the spectrum of atomic hydrogen the wave number of each line is given by ¯¯¯V=R[1n21−1n22] where RH is a constant and n1 and n2 are integers. Which of the following statements (s), is (are correct)
1. As wave length decreases the lines in the series converge
2. The integer n1 is equal to 2.
3. The ionisation energy of hydrogen can be calculated from the wave numbers of three lines.
4. The line of shortest wavelength corresponds to = 3.A1, 2 and 3B2, 3 and 4C1, 2 and 4D2 and 4 onlyFor balmer series in the spectrum of atomic hydrogen the wave number of each line is given by
¯¯¯V=RH1n21−1n22 where RH is a constant and n1 and n2 are integers which of the following statement (S) is / are correct
1 as wavelength decreases the lines in the series converge
2 The integer n1 is equal to 2
3 The ionization energy of hydrogen can be calculated from the wave number of these lines
4 The line of longest wavelength corresponds to n2=3A1,2 and 3B2,3 and 4C1,2 and 4D2 and 4 onlyFor Balmer series in the spectrum of atomic hydrogen, the wave number of each line is given by v=RII(1n21−1n22) where RII is a constant and n1andn2 are integers. Which of the following statement (s) is (are) correct ?
(i) As wavelength decreases, the lines in the series converge.
(ii) The interger n1 is equal to 2.
(iii) The ionization energy of hydrogen can be calculated from the wave number of these lines.
(iv) The line of longest wavelength corresponds to n2=3.A(i), (ii) and (iii)B(ii), (iii) and (iv)C(i), (ii) and (iv)D(ii) and (iv)
For the Paschen series thr values of n1 and n2 in the expression ΔE=RHc[1n21−1n22] are
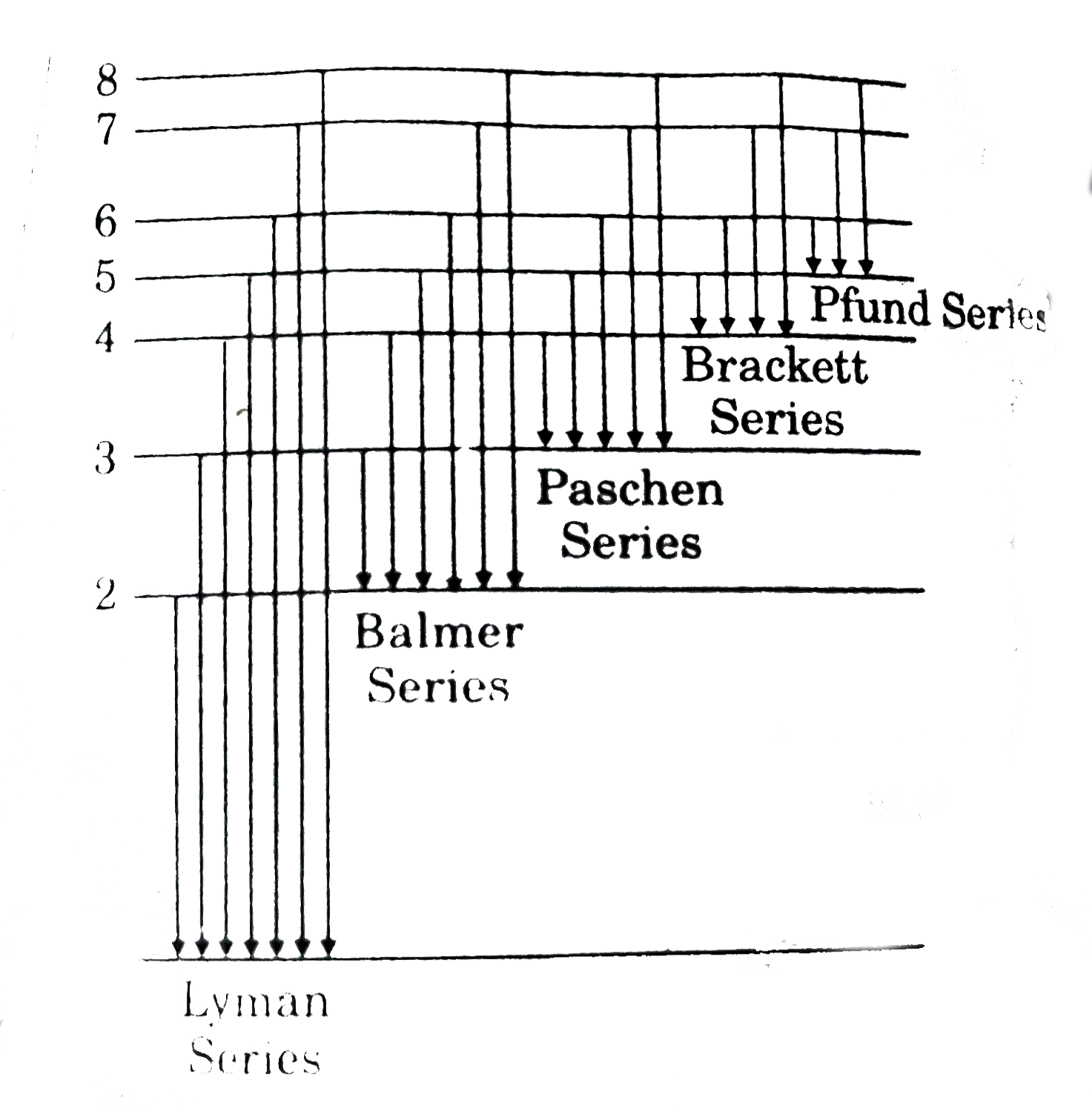
View Solutionthe only electron in the hydrogen atom resides under ordinary conditions in the first orbit. When energy is supplied the electron moves to higher energy orbit depending on the amount of energy absorbed. It emits energy. Lyman series is formed when the electron returns to the lowest orbit while Balmer series is formed when the electron returns to second. Similarly, Paschen, Breakett and Pfund series are formed when electron returns to the third, fourth and fifth orbits from higher energy orbits respectively (as shown in figure).

Maximum number of different lines produced when electron jump from nth level to ground level is equal to
n(n−1)2.
For example in the case of n=4, number of lines produced is 6.(4→3,4→2,4→1,3→2,3→1,2→1).When an electron returns from n2ton1 state, the number of different
lines in the spectrum will be equal to (n2−n1)(n2−n1+1)2
If the electron comes back from energy level having energy E2 to energy level having energy E1, then the difference may be expressed in terms of energy of photon as:
E2−E1=ΔE,λ=hcΔE,ΔE=hv(v−frequency)
Since h and c are constants ΔE corresponds to definite energy: thus each transition from one energy level to another will produce a light of definite wavelength. This is actually observed as a line in the spectrum of hydrogen atom.
Wave number of line is given by the formula:
¯v=RZ2(1n21−1n22)
where R is a Rydberg constant (R=1.1×107m−1).
(i) First line of a series : It is called line of longest wavelength of line of smallest energy'.
(ii) Series limit or last line of a series : It is the line of shortest wavelength or line of highest energy.
Last line of breakett series for H-atom has wavelength λ1Å and 2nd line of Lyman series has wavelength λ2Åthen:
View Solutionthe only electron in the hydrogen atom resides under ordinary conditions in the first orbit. When energy is supplied the electron moves to higher energy orbit depending on the amount of energy absorbed. It emits energy. Lyman series is formed when the electron returns to the lowest orbit while Balmer series is formed when the electron returns to second. Similarly, Paschen, Breakett and Pfund series are formed when electron returns to the third, fourth and fifth orbits from higher energy orbits respectively (as shown in figure).
Maximum number of different lines produced when electron jump from nth level to ground level is equal to
n(n−1)2.
For example in the case of n=4, number of lines produced is 6.(4→3,4→2,4→1,3→2,3→1,2→1).When an electron returns from n2ton1 state, the number of different
lines in the spectrum will be equal to (n2−n1)(n2−n1+1)2
If the electron comes back from energy level having energy E2 to energy level having energy E1, then the difference may be expressed in terms of energy of photon as:
E2−E1=ΔE,λ=hcΔE,ΔE=hv(v−frequency)
Since h and c are constants ΔE corresponds to definite energy: thus each transition from one energy level to another will produce a light of definite wavelength. This is actually observed as a line in the spectrum of hydrogen atom.
Wave number of line is given by the formula:
¯v=RZ2(1n21−1n22)
where R is a Rydberg constant (R=1.1×107m−1).
(i) First line of a series : It is called line of longest wavelength of line of smallest energy'.
(ii) Series limit or last line of a series : It is the line of shortest wavelength or line of highest energy.
wave number of the first line of Paschen series in Be3+ ion is :
View SolutionFor the Paschen series the values of n1 and n2 in the expression ΔE=RH.c(1n21−1n22)
View Solutionthe only electron in the hydrogen atom resides under ordinary conditions in the first orbit. When energy is supplied the electron moves to higher energy orbit depending on the amount of energy absorbed. It emits energy. Lyman series is formed when the electron returns to the lowest orbit while Balmer series is formed when the electron returns to second. Similarly, Paschen, Breakett and Pfund series are formed when electron returns to the third, fourth and fifth orbits from higher energy orbits respectively (as shown in figure).
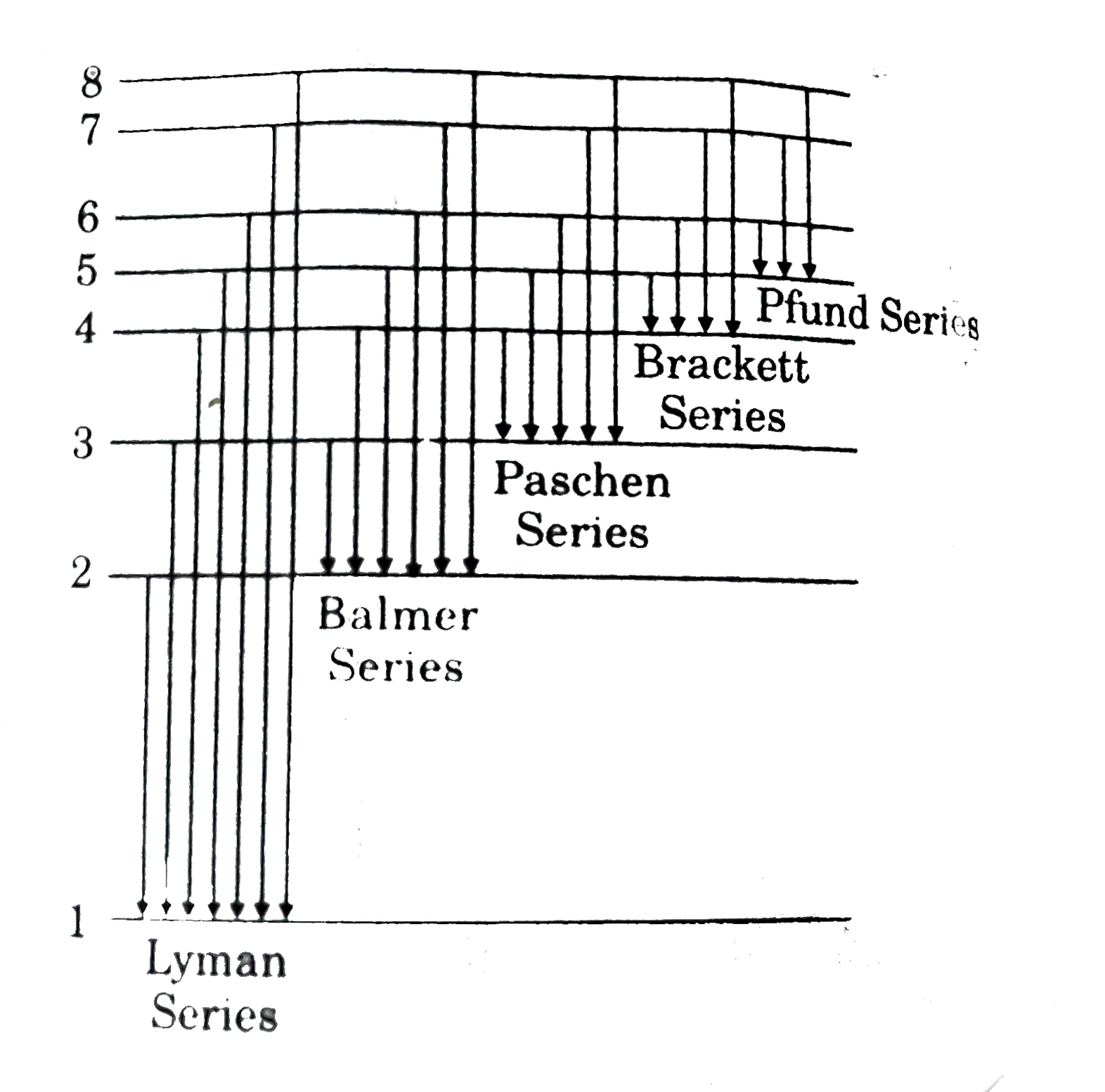
Maximum number of different lines produced when electron jump from nth level to ground level is equal to
n(n−1)2.
For example in the case of n=4, number of lines produced is 6.(4→3,4→2,4→1,3→2,3→1,2→1).When an electron returns from n2ton1 state, the number of different
lines in the spectrum will be equal to (n2−n1)(n2−n1+1)2
If the electron comes back from energy level having energy E2 to energy level having energy E1, then the difference may be expressed in terms of energy of photon as:
E2−E1=ΔE,λ=hcΔE,ΔE=hv(v−frequency)
Since h and c are constants ΔE corresponds to definite energy: thus each transition from one energy level to another will produce a light of definite wavelength. This is actually observed as a line in the spectrum of hydrogen atom.
Wave number of line is given by the formula:
¯v=RZ2(1n21−1n22)
where R is a Rydberg constant (R=1.1×107m−1).
(i) First line of a series : It is called line of longest wavelength of line of smallest energy'.
(ii) Series limit or last line of a series : It is the line of shortest wavelength or line of highest energy.
Consider the following statements
(i) Spectral lines of He+ion belonging to Balmer series are not in visible range.
(ii) In the Balmer series of H-atom maximum lines are in ultraviolet ragion.
(iii) 2nd line of Lyman series of He+ ion has energy 48.35eV
The above statement (i), (ii), (iii) respectively are(T=True,F=False):
View Solution
