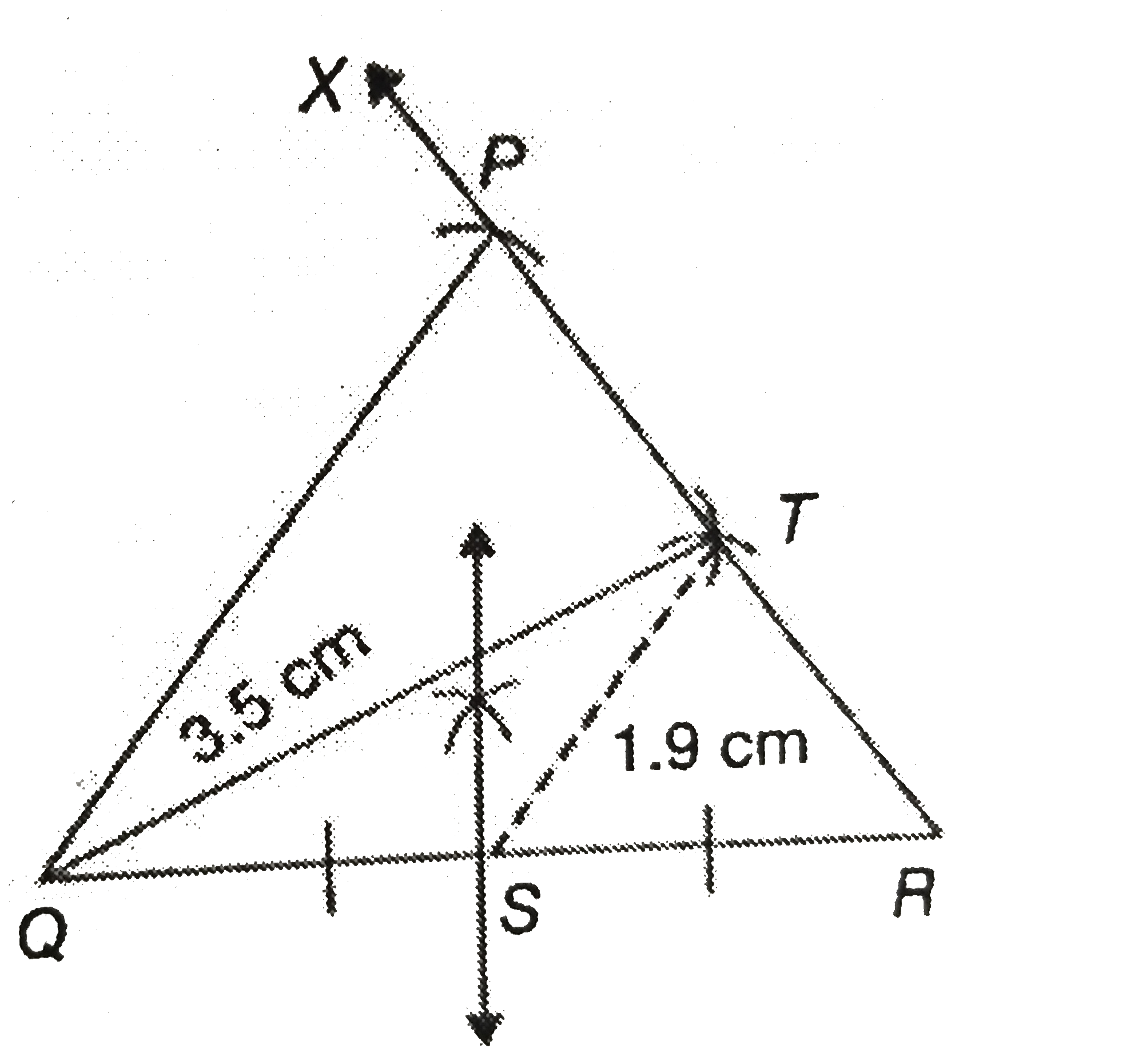
Construct a triangle PQR, such that PQ=38cm, QR=4.3cm and the median from Q to PR is 3.5cm.
Step 1: Draw a line segment QR of length 43cm.
Step 2: Draw the perpendicular bisector of ¯¯¯¯¯¯QR and mark the mid-point of QR as S.
Step 3: Taking Q as the center and radius equal to 3.5cm, draw an arc.
Step 4: Taking S as the center and radius =1.9cm (12PQ), draw another arc intersecting the already drawn arc (in Step 3) at T.
Step 5: Join R and T and produce RT to X.
Step 6: With Q as the center and radius =3.8 cm, draw an arc to intersect ¯¯¯¯¯¯RX at P. Join PQ. △PQR is the required triangle.
Topper's Solved these Questions
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - TEST YOUR CONCEPTS
29 Videos
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - SHORT ANSWER TYPE QUESTIONS
18 Videos
- COORDINATE GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - Level 3
9 Videos
- LINEAR EQUATIONS AND INEQUATIONSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LINEAR EQUATIONS AND INEQUATIONSEXERCISE - level 3
10 Videos
Similar Questions
Construct a triangle PQR such that PQ=6 cm, QR=7cm and PR=4.5cm.
View SolutionConstruct a parallelogram PQRS such that PQ=5cm, PR=7cm and QS=8cm.
View SolutionConstruct a parallelogram PQRS, when PQ =3.7cm, QR =2.3 cm and PR=4.8 cm.
View SolutionConstruct a triangle PQR with sides PQ = 5 cm, QR = 4 cm, and ∠PQR=100∘.
View SolutionConstruct a triangle PQR, in which PR=6cmandPQ=QR=6.8cm.
Mark S the mid-point of PQ.
View SolutionConstruct a triangle PQR, in which QR=4.5cm, ∠Q=44∘ and PQ−PR=2cm.
View SolutionConstruct a rectangle PQRS with PQ=5.3 cm and diagonal PR=5.8 cm.
View SolutionConstruct a triangle PQR in which QR=4.7 cm PR−PQ=2.3cm and ∠Q−∠R=50∘.
View SolutionConstruct a triangle PQR given that PQ = 5 cm, QR = 4 cm and PR = 3 cm . Measure ∠PRQ and name the triangle.
View SolutionConstruct a triangle PQR in which QR = 6cm, ∠Q=60∘ and PR – PQ = 2cm.
View Solution
