A straight highway leads to the foot of a tower of height 50 m. From the top of tower, the angles of depression of two cars standing on the highway are 30∘ and 60∘ respectively. What is the distance between the two cars and how far is each car from the tower?
100√3
50√3
50√3
100√3
The correct Answer is:D
Use tanθ = opposite side/adjacent side in the triangle so formed.
Topper's Solved these Questions
Similar Questions
A straight highway leads to the foot of a tower of height 50 m. From the top of the tower, the angles of depression of two cars standing on the highway are 30o and 60o respectively. What is the distance between the two cars and how far is each car from the tower?
View SolutionFrom the top of a 96 m tower, the angles of depression of two cars, on the same side of the tower are α and βrespectively. If tanα=14 and tanβ=17, then find the distance between two cars.
View Solution
Knowledge Check
A straight highway leads to the foot of a tower of height 50 m . From the top of the tower, angles of depressions of two cars standing on the highway are 30∘and60∘ , What is the distance between the cars ?
A100 mB125 mC50√3mD150 mA straight highway leads to the foot of a tower of height 50 m. From the top of tower, the angles of depression of two cars standing on the highway are 30∘ and 60∘ respectively. What is the distance between the two cars and how far is each car from the tower?
A100√3mB100√3mC86.50 mDNone of theseFrom the top of a tower of height 180 m the angles of depression of two objects on either sides of the tower are 30∘and45∘ . Then the distance between the objects are
A180(3+√3)mB180(3−√3)mC180(√3−1)mD180(√3+1)m
From the top of a cliff 90 m high, the angles of depression of the top and bottom of a tower are observed to be 30∘ and 60∘ respectively. The height of the tower is :
View SolutionFrom the top of the cliff 150 m high, the angles of depression of the top and bottom of a tower are observed to be 30° and 60°, respectively. The height of the tower is
View SolutionTwo ships A and B are sailing straight away from the foot of a tower OP along routes such that ∣AOB––––––– is always 120∘. At a certain instance, the angles of depression of the ships A and B from the top P of the towers are 60∘and30∘ respectively. The distance between the ships when the height of the tower is 15m is
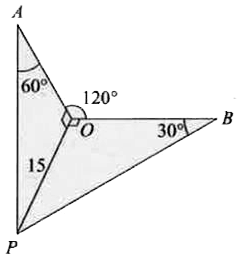
View SolutionFrom the top of a building, the angle of elevation and depression of top and bottom of a tower are 60∘and30∘ respectively. If the height of the building is 5 m, then find the height of the tower.
View SolutionThe angles of elevation of the top of a tower at the top and the foot of a pole 10 m high are 30∘and60∘ respectively. The height of the tower is
View Solution
