If cotθ=247 and θ is not in the first quadrant, then find the value of tanθ−secθ
A
1
B
43
C
32
D
54
Video Solution
Text Solution
The correct Answer is:B
Given, ∴sinθ=12⇒θ=30∘
As cotθ=247tanθ is positive and θ∉Q1,
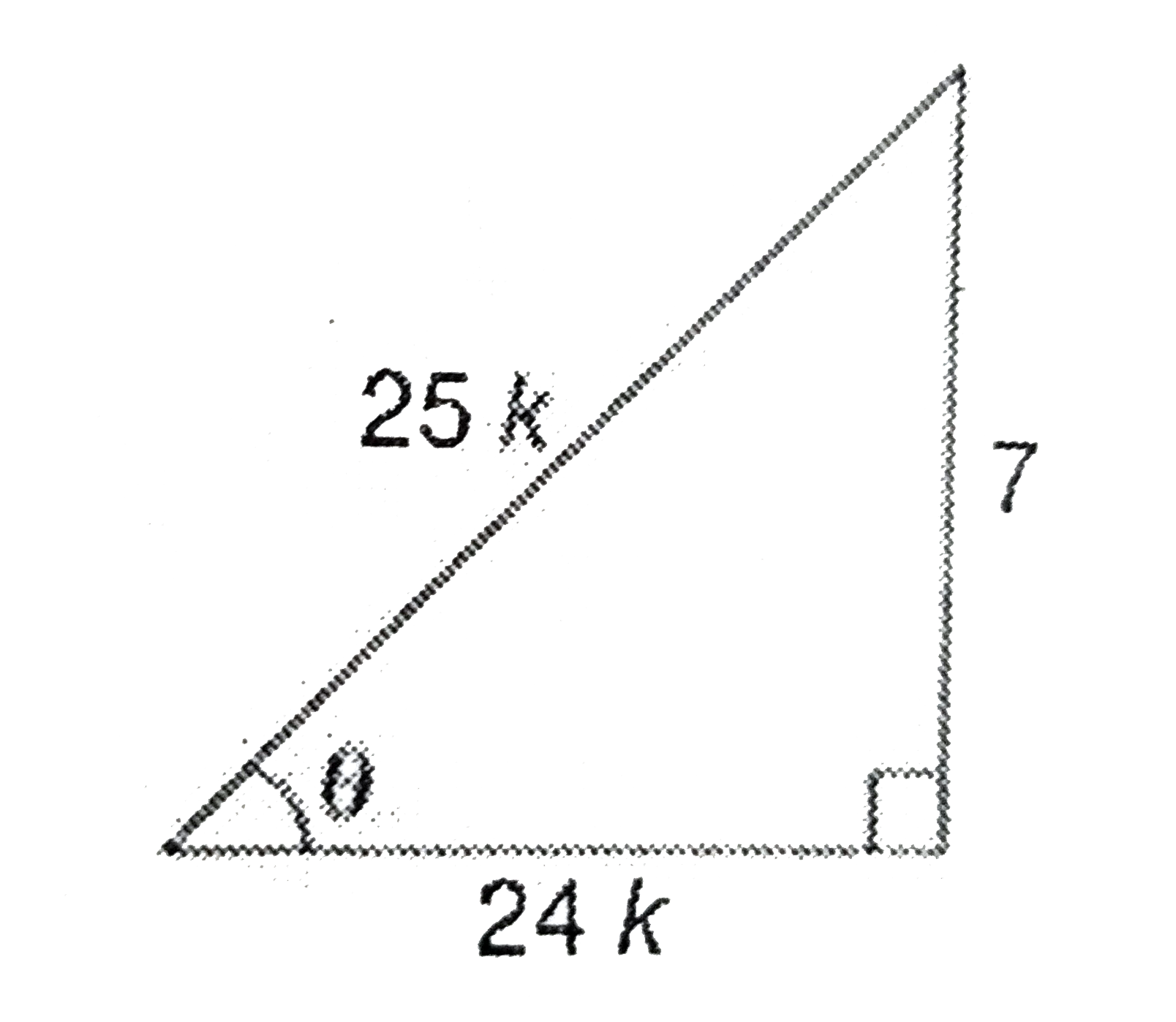
θ∉Q3⋅
∴secθ=−2524
tanθ=724
Now tanθ−secθ=724+2524
=3224=43
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If secθ+tanθ=3, then find the value of secθ.
A34B53C16D9 - Question 2 - Select One
If secθ+tanθ=2, then find the value of sinθ.
A35B23C−35D−25
If sinθ=35, then find the value of tanθandsecθ.
View SolutionIf cotθ=−125 and θ lies in the second quadrant,find the values of the other five functions.
View SolutionIf cotθ=43andθ is acute, then find the value of tanθ+cotθsecθ+cosecθ.
View SolutionIf tanθ=√2−1,then find the value of cotθ.
View SolutionIf secθ+tanθ=p. Then find the value of tanθ.
View SolutionIf tanθ=724andθ lie in 3rd quadrant, then the value of sinθ−cosθ will be-
View Solution

