A load of 600 kgwt is raised over an inclined plane as shown in the following figure.
How much force forming a couple should act on the pulley so that the load is just raised?
(i) Use the definition of mechanical advantage and principle of moments.
(ii) Calculate the effort (E) required to pull the load, using E = mg .
(iii) Part of the total force required to pull the load is provided by 100 kgwt.
(iv) Calculate the remaining force by .
(v) forms anti-clockwise moment on the pulley, where R = radius of the pulley.
(vi) Let be the force forming a couple so that the load is just raised.
(vii) Calculate using : .
(viii) 1000 N.
Topper's Solved these Questions
- SIMPLE MACHINESBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - SIMPLE MACHINESEXERCISE - Level- 2
25 Videos
- MODERN PHYSICSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MODERN PHYSICSEXERCISE - Level 3
5 Videos
- WAVES MOTION AND SOUND BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - WAVES MOTION AND SOUND EXERCISE - Level 3
10 Videos
Similar Questions
In the following figure :
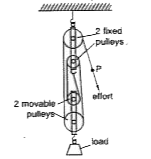
How far does the point P have to move down in order to raise the load by 1 m?
View SolutionA block of mas M is resting on an inclined plane as shown in the figure. The inclination of the plane to the horizontal is gradually increased. It is found that when the angle of inclination is θ the block just begins to slide down the plane. What is the minimum force F applied parallel to the plane that would just make the block move up the plane ?
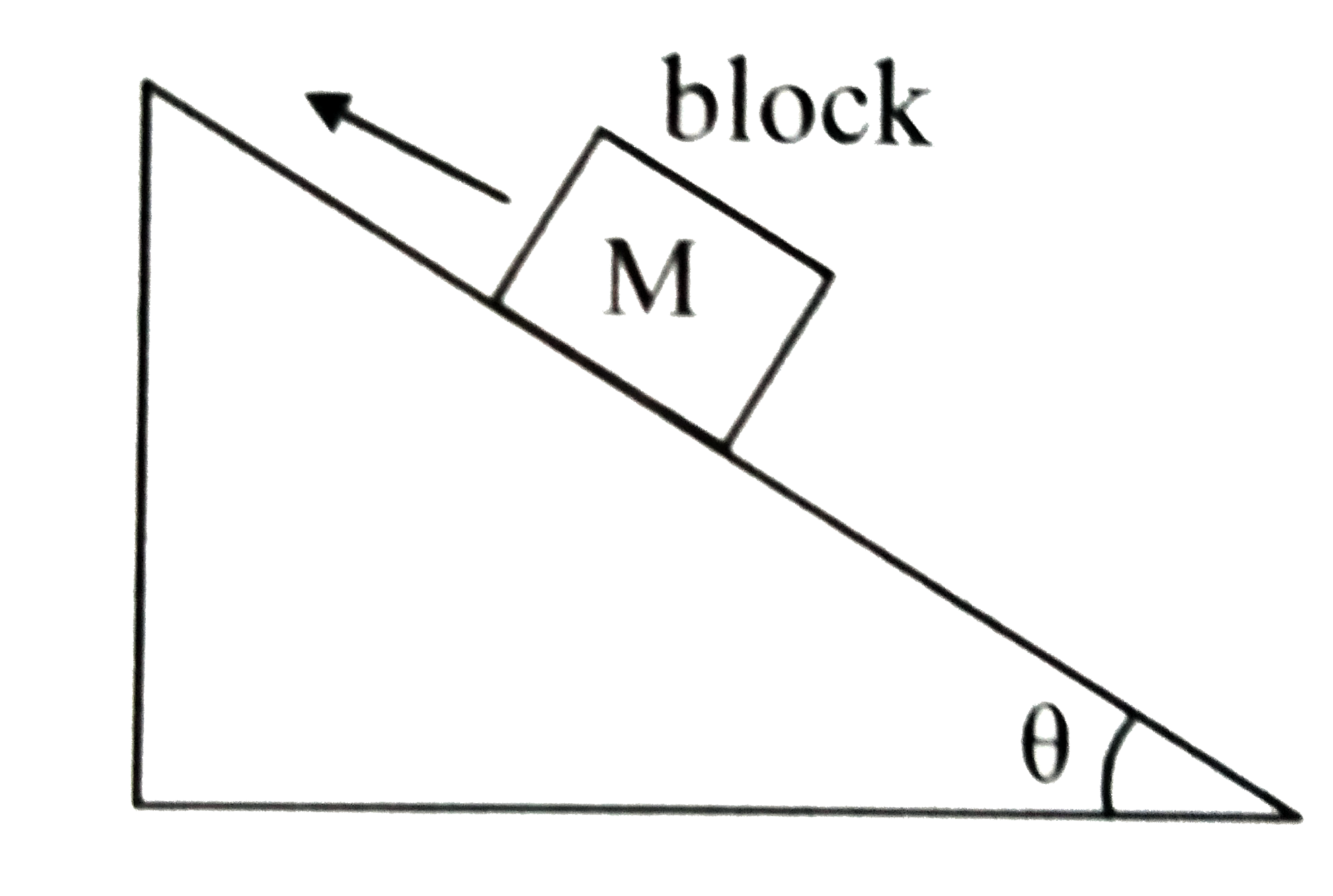
View Solution
Knowledge Check
A block of mass m = 4 kg is placed over a rough inclined plane as shown in figure. The coefficient of friction between the block and the plane is u=0.5. A force F= 10 N is applied on the block at an angle of 30°. The friction force between the block and wedge is
Astatic in nature in the direction up the plane and have the value 30.2 NBstatic in nature in the direction down the plane and have the value 30.2 NCkinetic in nature in the direction up the plane and have the value 13.5 NDNone of theseA horizontal force acting on a block of mass m which is placed on an inclined plane (as shown in the figure). What is the normal reaction N on the block?
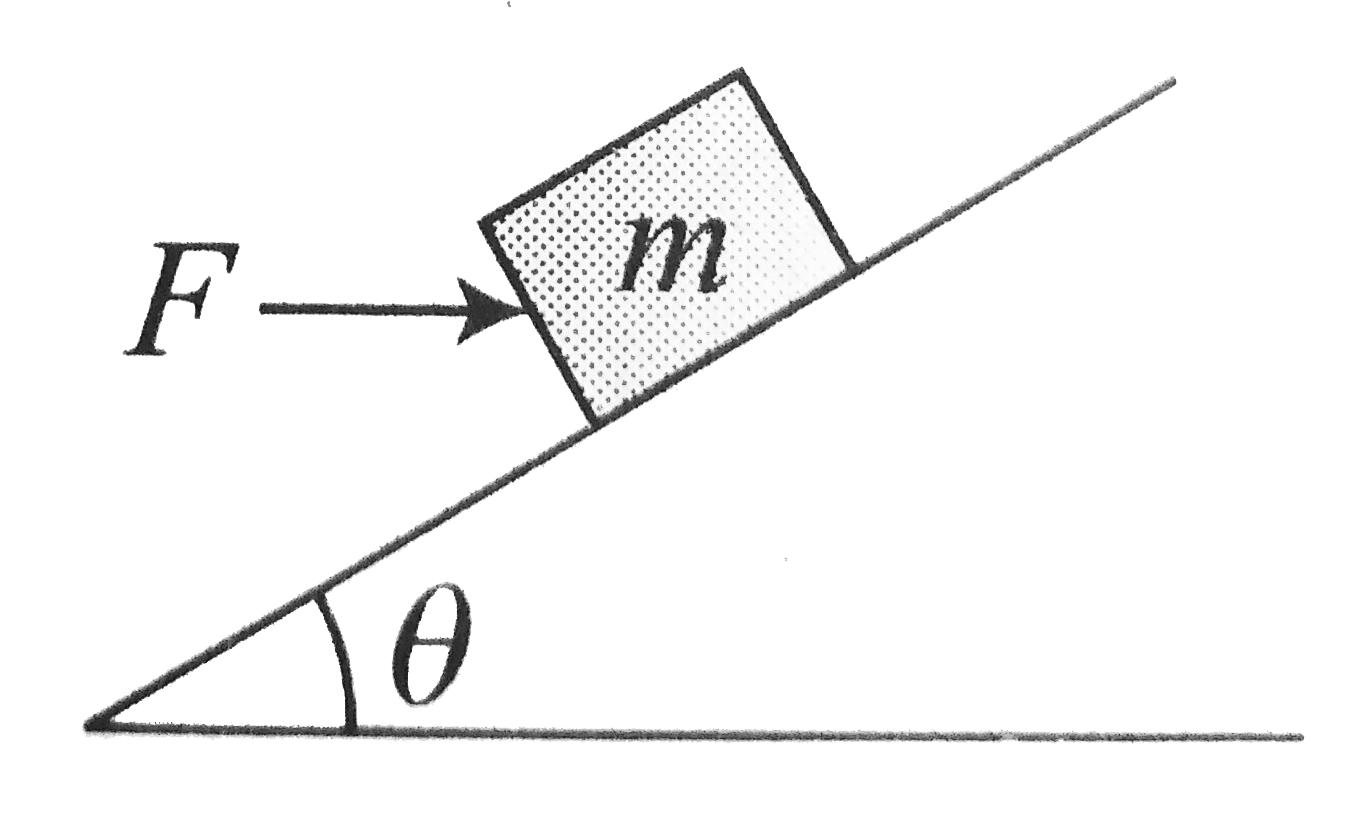Amgsinθ+FcosθBmgcosθ−FsinθCmgcosθ+FsinθDmgsinθ−FcosθA block of mass 10 kg is released from top of rough inclined plane as shown in the figure if coefficient of friction between the block and inclined plane is then total work done on the block by all the forces acting on it till it reaches the bottom s = 10 ms
A200 jB300 jC100 jD-200 j
A solid cylinder of mass m is wrapped with an inextensible light string and, is placed on a rough inclined plane as shown in the figure. The frictional force acting between the cylinder and the inclined plane is :
[The coefficient of static friction, μs is 0.4]
View SolutionA block of mas M is resting on an inclined plane as shown in the figure. The inclination of the plane to the horizontal is gradually increased. It is found that when the angle of inclination is θ the block just begins to slide down the plane. What is the minimum force F applied parallel to the plane that would just make the block move up the plane ?
View SolutionA block of mass m=2kg is resting on a inclined plane of inclination 30∘ as shown in figure The coefficient of friction between the block and the plane is μ=0.5 what minimum force F (in newton) should be applied perpendicular to the plane on the block so that the does not slip on the plane?
View SolutionTwo blocks of masses mi=2kg and m2=4kg hang, over a massless pulley as shown in the figure. A force F0=100N acting at the axis of the pulley accelerates the system upwards Then :
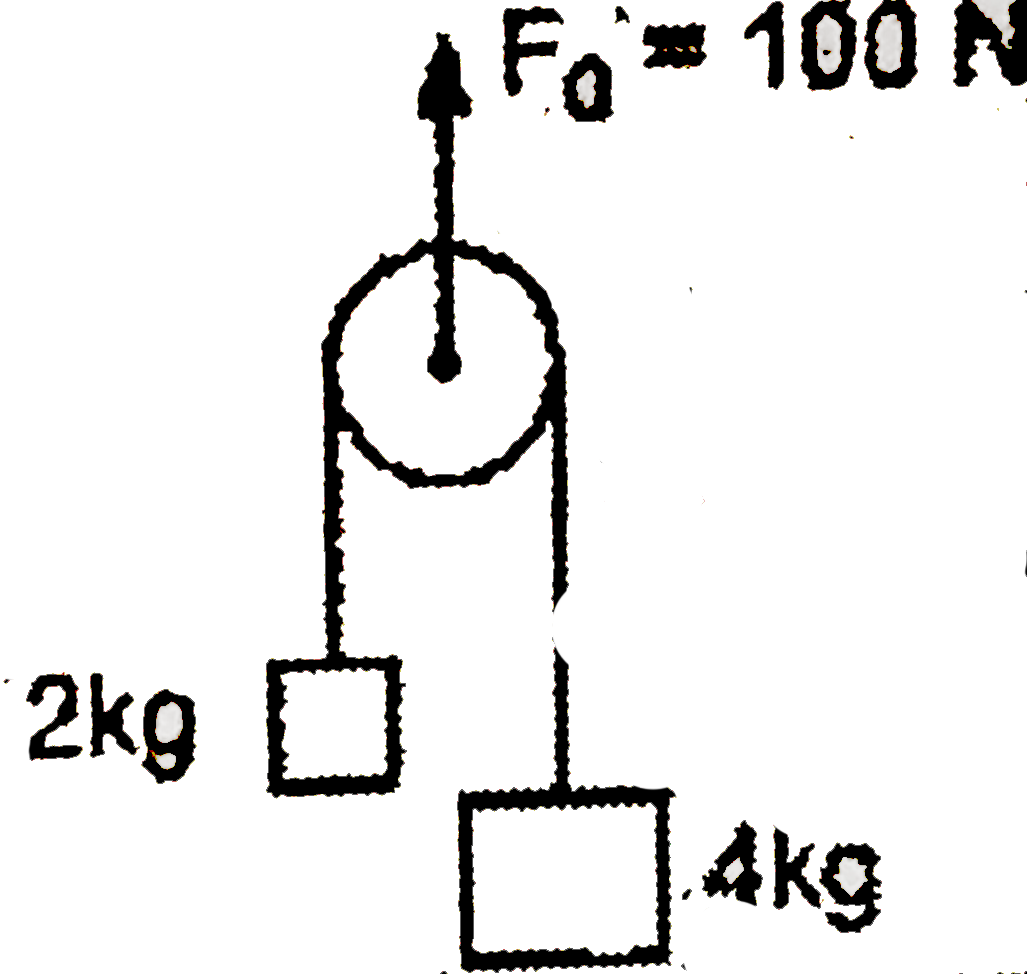
View SolutionA block of mass m=2kg is resting on a rough inclined plane of inclination of 30∘ as shown in figure. The coefficient of friction between the block and the plane is μ=0.5. What minimum force F should be applied perpendicular to the plane on the block, so that blocks does not slip on the plane? (g=10m/s2)
View Solution