State the conditions for stable, unstable and neutral equilibria.
To state the conditions for stable, unstable, and neutral equilibrium, we can follow these steps:
1. Understanding Equilibrium:
- Equilibrium occurs when the net force acting on a body is zero. This means the body is at rest, or moving with constant velocity.
2. Stable Equilibrium:
- A body is said to be in stable equilibrium if, when displaced slightly from its mean position, it experiences a restoring force that returns it to that position.
- Condition: The second derivative of potential energy with respect to displacement is positive:
d2Uds2>0
- This indicates that the potential energy is at a minimum at the equilibrium position.
3. Unstable Equilibrium:
- A body is in unstable equilibrium if, when displaced slightly from its mean position, it experiences a force that moves it further away from that position.
- Condition: The second derivative of potential energy with respect to displacement is negative:
d2Uds2<0
- This indicates that the potential energy is at a maximum at the equilibrium position.
4. Neutral Equilibrium:
- A body is in neutral equilibrium if, when displaced slightly from its mean position, it neither returns to its original position nor moves further away; it remains in its new position.
- Condition: The second derivative of potential energy with respect to displacement is zero:
d2Uds2=0
- This indicates that the potential energy is constant in the vicinity of the equilibrium position.
Summary of Conditions:
- Stable Equilibrium: d2Uds2>0 (Potential energy is at a minimum)
- Unstable Equilibrium: d2Uds2<0 (Potential energy is at a maximum)
- Neutral Equilibrium: d2Uds2=0 (Potential energy is constant)
- Equilibrium occurs when the net force acting on a body is zero. This means the body is at rest, or moving with constant velocity.
- A body is said to be in stable equilibrium if, when displaced slightly from its mean position, it experiences a restoring force that returns it to that position.
- Condition: The second derivative of potential energy with respect to displacement is positive:
d2Uds2>0
- This indicates that the potential energy is at a minimum at the equilibrium position.
- A body is in unstable equilibrium if, when displaced slightly from its mean position, it experiences a force that moves it further away from that position.
- Condition: The second derivative of potential energy with respect to displacement is negative:
d2Uds2<0
- This indicates that the potential energy is at a maximum at the equilibrium position.
- A body is in neutral equilibrium if, when displaced slightly from its mean position, it neither returns to its original position nor moves further away; it remains in its new position.
- Condition: The second derivative of potential energy with respect to displacement is zero:
d2Uds2=0
- This indicates that the potential energy is constant in the vicinity of the equilibrium position.
- Stable Equilibrium: d2Uds2>0 (Potential energy is at a minimum)
- Unstable Equilibrium: d2Uds2<0 (Potential energy is at a maximum)
- Neutral Equilibrium: d2Uds2=0 (Potential energy is constant)
Topper's Solved these Questions
- GRAVITATIONBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GRAVITATIONEXERCISE - ESSAY TYPE QUESTIONS
5 Videos
- GRAVITATIONBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GRAVITATIONEXERCISE - LEVEL-1
44 Videos
- GRAVITATIONBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GRAVITATIONEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
30 Videos
- ElectricityBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - ElectricityEXERCISE - Level 3
10 Videos
- HEATBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - HEATEXERCISE - All Questions
115 Videos
Similar Questions
For the potential energy curve shown shown in figure.
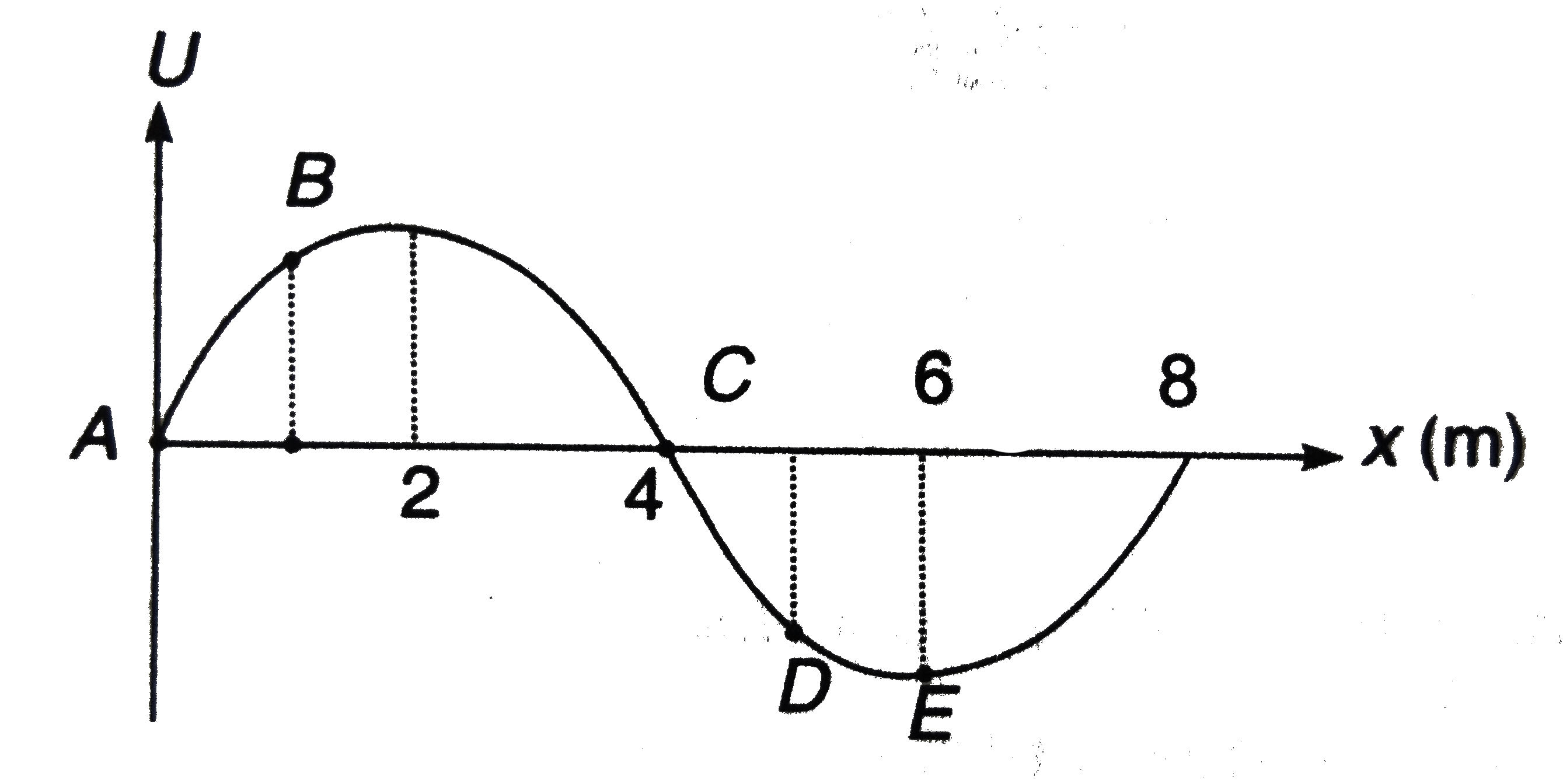
(a) Find directions of force at points A,B,C,D and E.
(b) Find positions of stable, unstable and neutral equilibriums.
View SolutionFor the potential energy curve shown in figure.
(a) Determine whether the force Fx is positive, negative, or zero at the five points indicated, (b) Indicate points of stable, unstable, and neutral equilibrium, (c) Sketch the curve for Fx versus x from x=0 to x=8m.
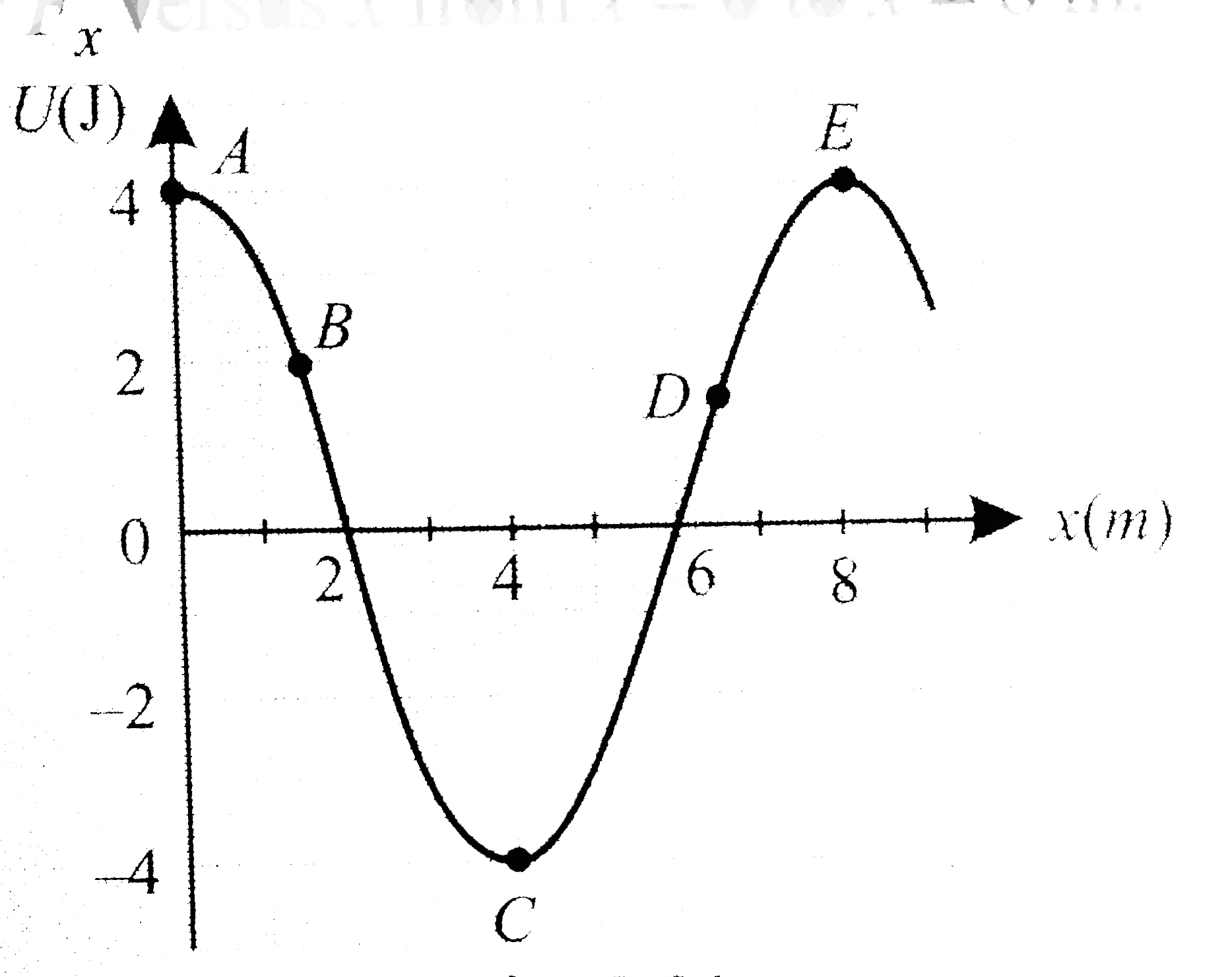
View Solution
Knowledge Check
potential enrgy of a particle along x-axis varies as, U=−20+(x−2)2, where U is in joule and x in meter. Find the equilibrium position and state whether it is stable or unstable equilibrium.
AU=-20Bx=2CU=+20Dx=-2
What are the conditions for stable and unstable equilibrium of a magnet suspended in a uniform magnetic field?
View SolutionDistinguish between stable, unstable and neutral equilibria of a body.
View SolutionDistinguish between stable, unstable and neutral equilibrium of a body
View SolutionState the condition for constructive interference.
View SolutionIn which orientation,a diole placed, in a uniform field is in (i) stable (ii) unstable equilibrioum?
View SolutionForce acting on a particle constrained to move along x-axis is F=(x−4). Here, F is in newton and x in metre. Find the equilibrium position and state whether it is stable or unstable equilibrium.
View SolutionTwo point charges +q and fixed at (a,0,0) and (−a,0,0). A third point charge −q is at origin. State whether ite equlilbrium is stable, unstable or neutral if it is slightly displaced:
(a) along x-axis. , (b) along y-axis.
View Solution
