Two identical containers A and B are filled with two different liquids of equal masses. The level of the liquid in container A is found to be one-fourth of the level of the liquid in container B. What is the ratio of thedensity of two liquids? If the density of he liquid in the container A is 2 " g "cm−3, then find the density of the mixture of the two liquids.
Mass of liquid A, (mA) = mass of liquid B, (mB)
Volume = area×height
Area of cross section of A = Area cross section of B
Height of liquid column A = 14× " height " of liquid column A = 14 (Volume of B) <br>Densityof"mass/volume"(density " of " A)/(density " of " B) = m_(A)/V_(A)xx V_(B)/m_(B)=V_(B)/V_(B)=4/1=4 :1<br>IfdensityofAis2 g cm^(-3),thendensityofB= g cm^(-3)=0.5 g cm^(-3)<br>Densityofmixture="mass of mixture"/"volume of mixture"<br>(m_(A)+m_(B))/(v_(A)+v_(B))=(m_(A)=m_(A))/(v_(A)=4v_(A)) ( :. m_(B) = m_(A) and v_(B)= 4v_(A))<br>(2m_(A))/(5v_(A)) = (2xx d_(A)xx v_(A))/(5V_(A)<br>(2xx2)/5=4/5=0.8 " g "cm^(-3)
Topper's Solved these Questions
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MEASUREMENTSEXERCISE - Test 130videos
MEASUREMENTS
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MEASUREMENTSEXERCISE - Test 230videos
MEASUREMENTS
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MEASUREMENTSEXERCISE - Level 2 (MCQs)58videos
MEASUREMENTS
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MACHINES AND TOOLSEXERCISE - CONCEPT APPLICATION (LEVEL 2)12videos
MACHINES AND TOOLS
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MOCK TESTEXERCISE - MULTIPLE CHOICE QUESTION25videos
MOCK TEST
Similar Questions
Two identical containers A and B are filled with two different liquids of equal masses. The level of the liquid in container A is found to be one-fourth of the level of the liquid in container B. What is the ratio of thedensity of two liquids? If the density of he liquid in the container A is 2 " g "cm−3, then find the density of the mixture of the two liquids.
View SolutionIn a Hare's apparatus when the air inside the tube is su c ked the differe nce in the level of water an d liquid in the container is found to be 3 cm and the difference in the tubes is fo u nd to be 4 cm. If th e level of water in tube is 16 cm. c.ilculate the relative density of the liquid. The den sity of liquid is m o re than the density of water and the level of liquid in the container is more than that of water.
View Solution
Knowledge Check
- Question 1 - Select One
The pressure exerted by a liquid column at the bottom of the liquid container is
Adoes not depend on the area of cross-section of container.Bdependent on the density of the liquid.Cequal in all directions.DAll the above are true - Question 2 - Select One
The liquid inside the container has density ρ. Choose the correct option.
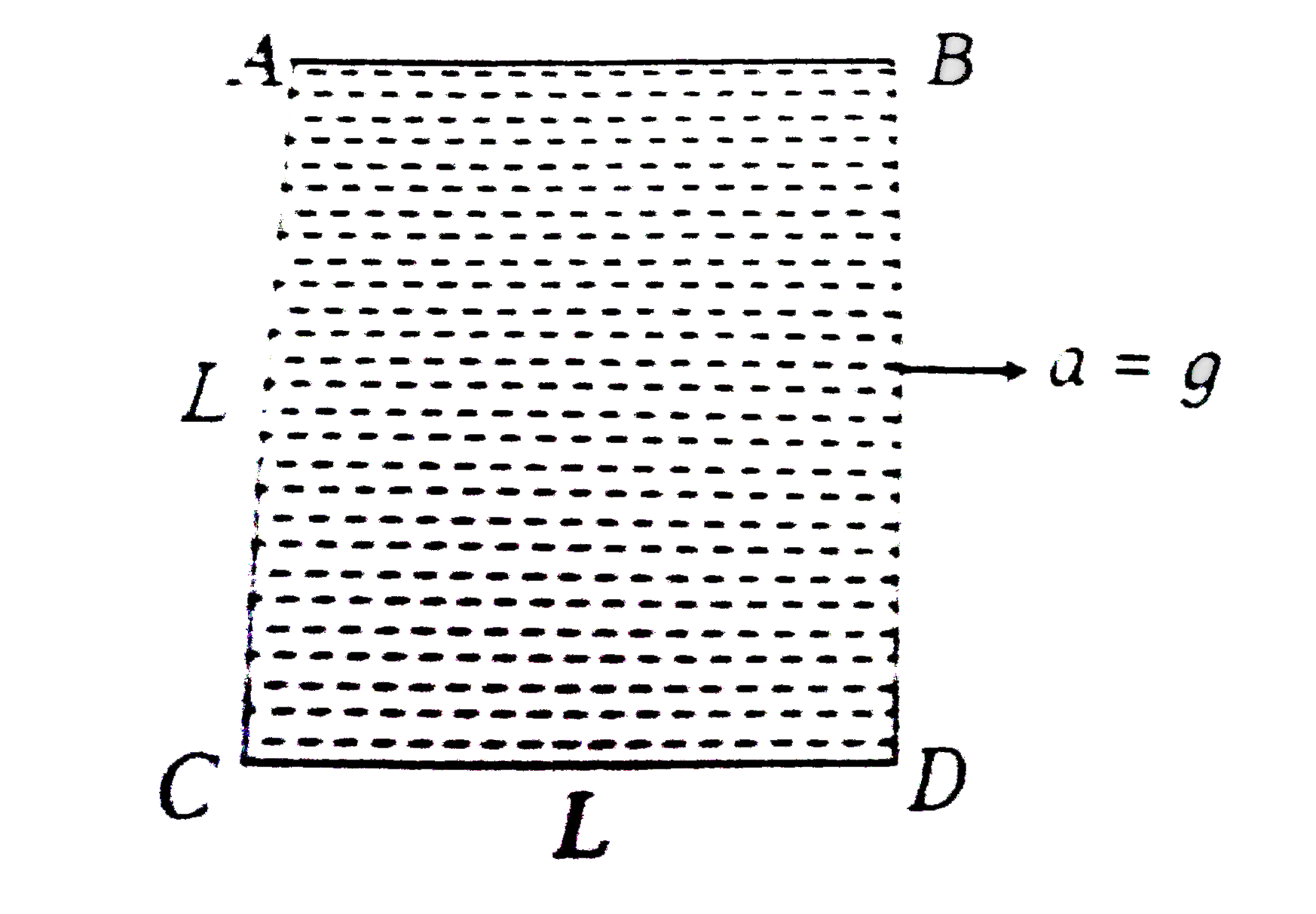 ApA−pC=2ρgLBpC−pB=√2ρgLCpC−pD=ρgLDpA−pD=0ρgL
ApA−pC=2ρgLBpC−pB=√2ρgLCpC−pD=ρgLDpA−pD=0ρgL - Question 3 - Select One
A container filled with a liquid A is floating on the surface of another liquid 'B' as shown in the figure, then volume of the liquid displaced by the container
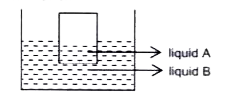 Ais equal to the volume of the liquid A.Bis greater than the volume of the liquid A.Cis less than the volume of the liquid A.DCannot be determined
Ais equal to the volume of the liquid A.Bis greater than the volume of the liquid A.Cis less than the volume of the liquid A.DCannot be determined
Two containers contain two liquids A and B. The mass of liquid A is half the mass of liquid B. Both of them are heated to that extent so that the increase in the temperatures of the liquids is the same. The heat supplied for this purpose in liquid A is double that in the case of liquid B. Find out the ratio of the specific heat of A and B.
View SolutionTest tube A contains 10 ml of liquid X and test tube B contains a liquid Y of volume 50 ml. the ratio o the density of Y to X is 2:5. Compare the mass of liquid A and B.
View SolutionA container filled with a liquid A is floating on the surface of another liquid 'B' as shown in the figure, then volume of the liquid displaced by the container
 View Solution
View SolutionThe liquid whose coeffcient of real expansion is equal to 1.5 times the coefficient of areal expansion of container and heated then the level of the liquid taken in the container
View SolutionA cube of ice is floating in a liquid of relative density 1.25 contained in a beaker . When the ice melts, the level of the liquid in the beaker ?
View Solution

