Let Sk denote sum of infinite geometric series (K=1,2,3,.......), where first term is (k2−1) and common ratio is 1K, then the unit digit of the sum (∞∑k=1Sk2k−1), is
Video Solution
|
Answer
Step by step video & image solution for Let S_(k) denote sum of infinite geometric series (K=1,2,3,.......), where first term is (k^(2)-1) and common ratio is (1)/(K), then the unit digit of the sum (sum_(k=1)^(oo)(S_(k))/(2^(k-1))), is by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023
Similar Questions
Knowledge Check
- Question 1 - Select One
The sum 20∑k=1k12k is equal to
A2−11219B1−11220C2−3217D2−21220 - Question 2 - Select One or More
Let Sk, be the sum of an infinite geometric series whose first term is kand common ratio is kk+1(k>0) . Then the value of ∞∑k=1(−1)kSk is equal to
A1−4loge√2Bloge2−1C1−loge2D1−loge4 - Question 3 - Select One
The Sum 20∑K=1K12K is equal to.
A2−3217B1−11220C2−11219D2−21220
Let Sk, where k=1,2,....,100, denotes the sum of the infinite geometric series whose first term is k−1k! and the common ratio is 1k. Then, the value of 1002100!+100∑k=2∣∣(k2−3k+1)Sk∣∣ is....
View SolutionFind the ∞∑k=1∞∑n=1k2n+k.
View SolutionThe sum n∑k=1k(k2+k+1) is equal to
View SolutionThe sum 100∑k=1kk4+k2+1 is equal to
View SolutionThe sum ∞∑k=1cot−1(2k2) equals
View Solution

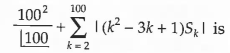 is
is