Let Sk, be the sum of an infinite geometric series whose first term is kand common ratio is kk+1(k>0) . Then the value of ∞∑k=1(−1)kSk is equal to
1−4loge√2
loge2−1
1−loge2
1−loge4
The correct Answer is:A, D
To solve the problem, we need to find the value of the sum:
∞∑k=1(−1)kSk
where Sk is the sum of an infinite geometric series with first term k and common ratio r=kk+1.
Step 1: Find Sk
The sum Sk of an infinite geometric series can be calculated using the formula:
S=a1−r
where a is the first term and r is the common ratio. Here, a=k and r=kk+1.
Substituting these values into the formula gives:
Sk=k1−kk+1=k1k+1=k(k+1)
Step 2: Substitute Sk into the sum
Now, we substitute Sk back into our original sum:
∞∑k=1(−1)kSk=∞∑k=1(−1)kk(k+1)
Step 3: Simplify the term 1k(k+1)
We can simplify 1k(k+1) using partial fractions:
1k(k+1)=1k−1k+1
Step 4: Rewrite the series
Now we can rewrite the sum:
∞∑k=1(−1)k(1k−1k+1)
This can be split into two separate sums:
∞∑k=1(−1)kk−∞∑k=1(−1)kk+1
Step 5: Change the index of the second sum
For the second sum, we can change the index by letting j=k+1:
∞∑k=1(−1)kk+1=∞∑j=2(−1)j−1j
Step 6: Combine the sums
Now we can combine the two sums:
∞∑k=1(−1)kk−∞∑j=2(−1)j−1j=∞∑k=1(−1)kk−(∞∑k=1(−1)kk−(−1)11)
This simplifies to:
∞∑k=1(−1)kk+1
Step 7: Evaluate the alternating series
The series ∞∑k=1(−1)kk is known to converge to −log(2). Thus, we have:
−log(2)+1
Final Result
Therefore, the final value of the sum is:
1−log(2)
Topper's Solved these Questions
- A.P.,G.P.,H.P.BOOK - MTG-WBJEECHAPTER - A.P.,G.P.,H.P.EXERCISE - WB JEE Previous Years Questions ( CATEGORY 1: Single Option Correct Type (1 Mark ) )
14 Videos
- A.P.,G.P.,H.P.BOOK - MTG-WBJEECHAPTER - A.P.,G.P.,H.P.EXERCISE - WB JEE Previous Years Questions ( CATEGORY 2 : Single Option Correct Type (2 Mark ) )
5 Videos
- A.P.,G.P.,H.P.BOOK - MTG-WBJEECHAPTER - A.P.,G.P.,H.P.EXERCISE - WB JEE WORKOUT ( CATEGORY 2 : Single Option Correct Type (2 Marks) )
15 Videos
- APPLICATION OF DERIVATIVES BOOK - MTG-WBJEECHAPTER - APPLICATION OF DERIVATIVES EXERCISE - WB JEE Previous Years Questions ( CATEGORY 3 : One or More than One Option Correct Type (2 Marks) )
11 Videos
Similar Questions
Let sk,k=1,2,3,…,100 denote the sum of the infinite geometric series whose first term is k−1⌊k and the common ratio is 1k. Then, the value of
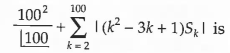 is
is
View SolutionLet Sk, where k=1,2,....,100, denotes the sum of the infinite geometric series whose first term is k−1k! and the common ratio is 1k. Then, the value of 1002100!+100∑k=2∣∣(k2−3k+1)Sk∣∣ is....
View Solution
Knowledge Check
Let SK be the sum of an infinte G.P. series whose first term is K and common ratio is KK+1(K>0). Then the value of ∞∑K=1(−1)KSK is equal to
Aloge4Bloge2−1Cloge2+1D1−loge4The sum 20∑k=1k12k is equal to
A2−11219B1−11220C2−3217D2−21220The Sum 20∑K=1K12K is equal to.
A2−3217B1−11220C2−11219D2−21220
Let Sk denote sum of infinite geometric series (K=1,2,3,.......), where first term is (k2−1) and common ratio is 1K, then the unit digit of the sum (∞∑k=1Sk2k−1), is
View SolutionThe sum 100∑k=1kk4+k2+1 is equal to
View SolutionThe sum n∑k=1k(k2+k+1) is equal to
View SolutionLet Sk be sum of an indinite G.P whose first term is 'K' and commmon ratio is 1k+1. Then Σ10k=1Sk is equal to _________.
View SolutionLet Sk, where k=1,2,....,100, denotes the sum of the infinite geometric series whose first term is k.k−1k! and the common ratio is 1k. Then, the value of 1002100!+100∑k=2∣∣(k2−3k+1)Sk∣∣ is....
View Solution
