புதிதாக உருவாக்கப்பட்ட ஒரு நகரத்தின் வாக்காளர்களின் எண்ணிக்கையின் (ஆயிரங்களில்) அதிகரிப்பு V(t)=30+12t2−t3,0≤t≤8 என்பதால் மதிப்பிடப்படுகின்றது. இங்கு t என்பது ஆண்டுகளை குறிக்கின்றது காலம் 4-இலிருந்து 416வருடமாக இருக்கும் போது ஏற்படும் தோராய வாக்காளர்களின் எண்ணிக்கை மாற்றத்தைக் காண்க.
Step by step video & image solution for புதிதாக உருவாக்கப்பட்ட ஒரு நகரத்தின் வாக்காளர்களின் எண்ணிக்கையின் (ஆயிரங்களில்) அதிகரிப்பு V(t)=30+12t^2-t^3, 0le t le 8 என்பதால் மதிப்பிடப்படுகின்றது. இங்கு t என்பது ஆண்டுகளை குறிக்கின்றது காலம் 4-இலிருந்து 4frac{1}{6}வருடமாக இருக்கும் போது ஏற்படும் தோராய வாக்காளர்களின் எண்ணிக்கை மாற்றத்தைக் காண்க. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
ஆதிப்புள்ளியிலிருந்து t வினாடிகளுக்குப் பிறகு ஒரு துகள் உள்ள தூரத்தின் அளவு s=2t2+3t மீட்டர் எனும்படி நேர்க்கோட்டில் ஒரு துகள் நகர்கிறது. t=3 மற்றும் t = 6 வினாடிகளுக்கிடையே உள்ள சராசரி திசைவேகம் என்ன?
View Solution→a மற்றும் →b என்பன இணைவெக்டர்கள் எனில், [→a→b→c]-ன் மதிப்பு காண்க.
View SolutionThe value of 3sin4t+cos4t−1sin6t+cos6t−1 is equal to __________
View Solutiont^(3)+t^(2)+t+6=0
View Solution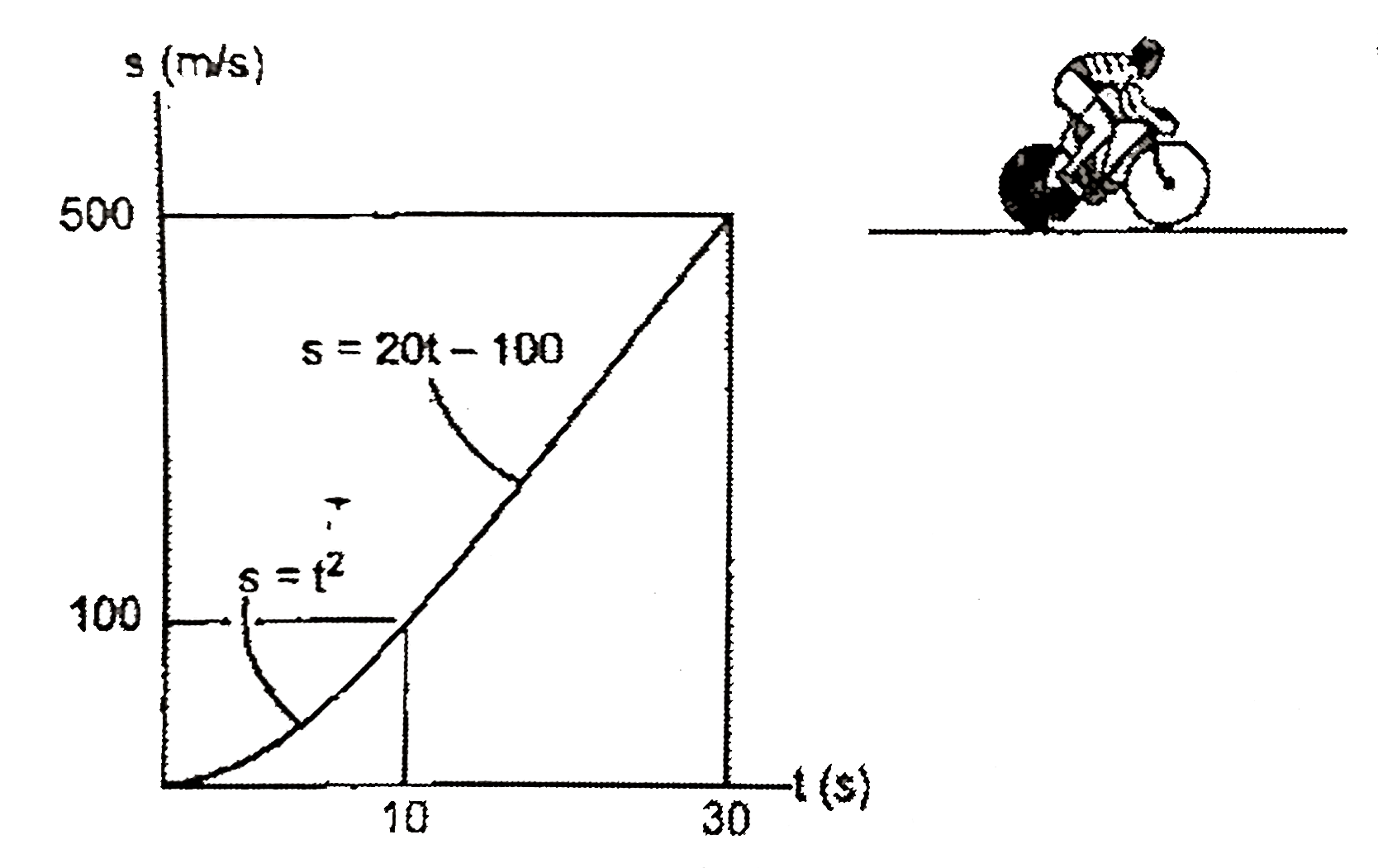
A bicycle moves along a stragith road such that its construct the v-t and a-t graphs for 0≤t≤30.
View SolutionIf T+1/T=8 then T^3+1/T^3=
View Solutionp (t ) को g (t ) से भाग दीजिए , जबकि p(t)=t4+t3+t2−5t+1 और g(t)=t+1.
View Solutionp (t ) को g (t ) से भाग दीजिए , जबकि p(t)=t4+t3+t2−5t+1 और g(t)=t+1.
View Solutionयदि (If) cosx=1−t21+t2 तथा (and) siny=2t1+t2,0≤t≤1 सिद्ध करें कि (Prove that) d2ydx2, t से स्वतंत्र है |
View Solutionयदि बिन्दुएँ (4, 7, 8), (-1, -2, 1), (2, 3, 4) और (1, 2, t) एकतलीय हों तो t होगा
View SolutionIn a newly developed city, it is estimated that the voting population (in thousands) will increase according to V(t)=30+12t2−t3,0≤t≤8 where t is the time in years. Find the approximate change in voters for the time change from 4 to 4(16) year.
View SolutionVerify that (AB)T=BTAT if A=(23−1415) and B=⎛⎜⎝123−326⎞⎟⎠
View SolutionIf g(x) = int_(0)^(x) f(t)dt whereas 1/2 le f(t) 1 , t in [0,1] And 0 le f(t) le 1/2 , t in (1,2] For then
View Solution((1-t^6)/(1-t))^3 In the spread of t^4 Is the coefficient of
View SolutionThe motion of a particle along the x-axis is described by the following velocity function
v(t)=⎧⎪ ⎪⎨⎪ ⎪⎩(t3+t2+1)0≤t<3sec(2t+5)3≤t<5sec(t2−6t)5≤tsec
where v is in m/sec and t is in second
If initially, the particle was at x=0, then the position of particle at t=2 second will be
View Solution
