Question

Sketch the curves and identify the region bounded
by the curves $x=\frac{1}{2},x=2,y=\log x$ and $y=2^x.$
Find the area of this region.

Answer

`((4-sqrt(2))/(log2)-(5)/(2)log2+(3)/(2))` sq units

Explanation

The required area is the shaded portion in following figure

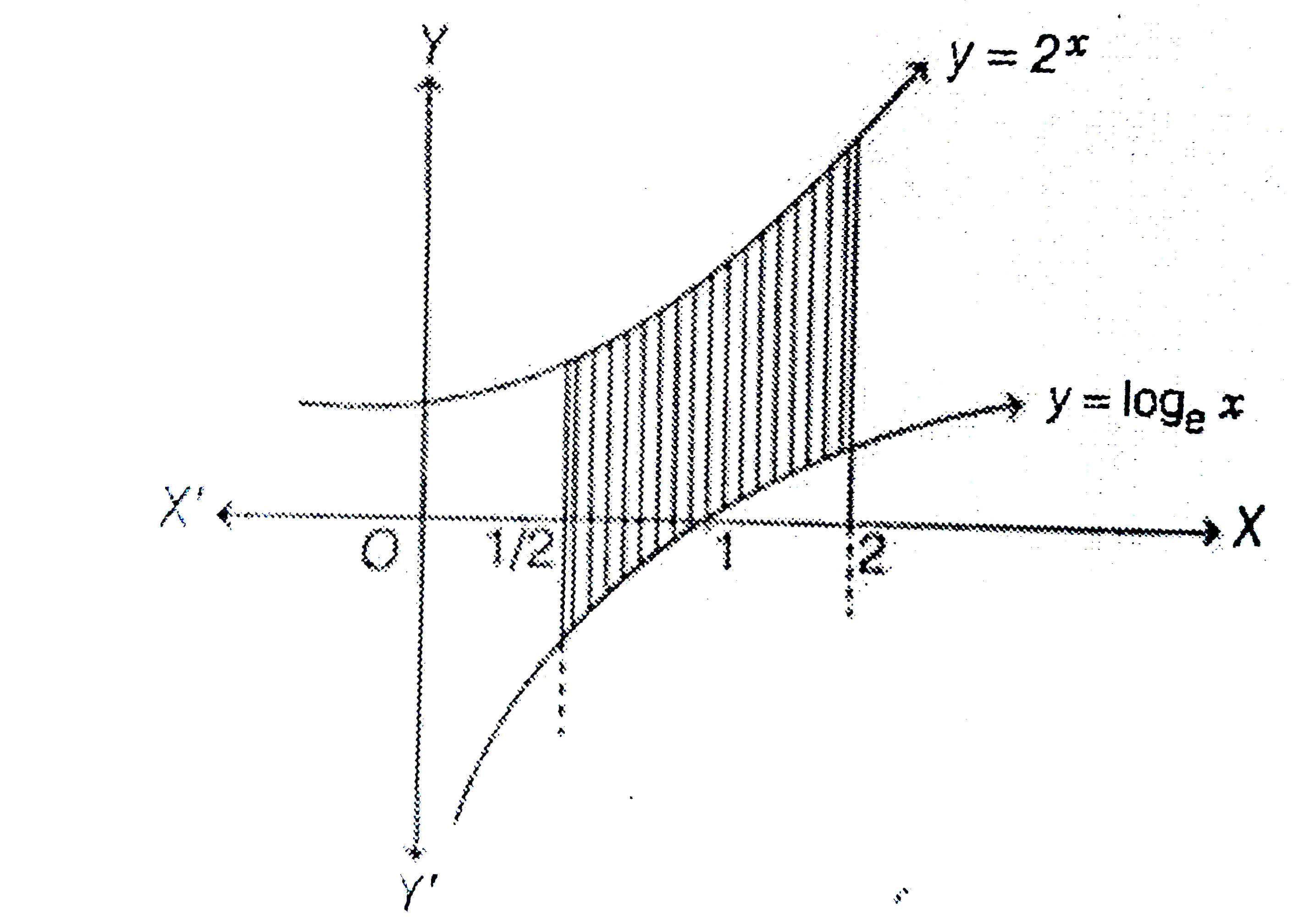
`therefore ` The required area
` = int_(1//2)^(2) (2^(x)-log)dx = ((2^(x))/(log2)-(x logx -x))_(1//2)^(2)`
` = ((4-sqrt(2))/(log2)-(5)/(2)log2+(3)/(2))` sq units