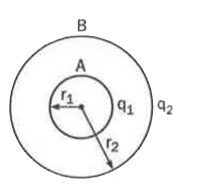
r1 व्यासार्ध और q1 आवेश वाले एक छोटे गोले के चारों ओर r2 व्यासार्थ और q2 आवेश वाला एक गोलीय खोल रख दिया जाता है [चित्र 12]| सिद्ध करें कि यदि q1 धनात्मक है , तो आवेश अवश्य ही गोले से गोलीय खोल की ओर बहेगा (जब दोनों को तार से जोड़ा जाए ) चाहे गोलीय खोल पर आवेश q2 कुछ भी हो।
बाहरी गोले B पर कुल विभव VB= इसके अपने आवेश q2 के कारण विभव + गोले A पर आवेश q1 के कारण विभव =14πε0[q2r2+q1r1]
आन्तरिक गोले A पर इसके अपने आवेश के कारण विभव
V1=14πε0q1r1
क्योंकि किसी आवेशित गोले के अंदर हर बिंदु पर विभव इसके पृष्ठ के विभव जितना होता है , इसलिए आन्तरिक गोले B पर आवेश q2 के कारण गोले A पर विभव
V2=14πε0q2r2
आन्तरिक गोले A पर कुल विभव
VA=14πε0[q1r1+q2r2]
इस प्रकार (VA−VB)=q14πε0(1r1−1r2)
क्योंकि r1<r2, इसलिए 1r1>1r2 या (1r1−1r2) धनात्मक है। साथ ही , q धनात्मक होने के कारण VA>VB है।
इस प्रकार जब दो गोले एक तार से जोड़े हैं ,तो गोले A पर सारे का सारा आवेश q1 गोले B की ओर बहेगा बावजूद इसके कि B पर आवेश q2 पहले से ही है। यह किसी भी आकर के चालकों के लिए सत्य है।
Topper's Solved these Questions
- धारिता और परावैधुत पदार्थ BOOK - GRB PUBLICATION HINDICHAPTER - धारिता और परावैधुत पदार्थ EXERCISE - प्रतियोगिता समाग्री (बहुविकल्पीय प्रश्न : एक सही विकल्प)
138 Videos
- धारिता और परावैधुत पदार्थ BOOK - GRB PUBLICATION HINDICHAPTER - धारिता और परावैधुत पदार्थ EXERCISE - प्रतियोगिता समाग्री (बहुविकल्पीय प्रश्न : एक या एक से अधिक सही विकल्प
35 Videos
- धारिता और परावैधुत पदार्थ BOOK - GRB PUBLICATION HINDICHAPTER - धारिता और परावैधुत पदार्थ EXERCISE - प्रतिरुपी अभ्यास
21 Videos
- धारा के चुम्बकीय प्रभावBOOK - GRB PUBLICATION HINDICHAPTER - धारा के चुम्बकीय प्रभावEXERCISE - NCERT पाठ्यपुस्तक अभ्यासः उत्तरों सहित
14 Videos
- नाभिक BOOK - GRB PUBLICATION HINDICHAPTER - नाभिक EXERCISE - प्रतियोगिता सामग्री (रिक्त स्थान भरना )
25 Videos
Similar Questions
चालक पेंट से कोट कि हुई एक टेबल - टेनिस की गेंद एक रेशमी धागे से लटकाई जाती है ताकि यह दो धातु की प्लेटों के बीच लटके। एक प्लेट को भूसंपर्कित किया जाता है। जबकि दूसरी एक उच्च वोल्टता जनित्र से जोड़ी जाती है। गेंद
View Solutionएक प्रोटॉन और एक इलेक्ट्रॉन , एकसमान वैधुत क्षेत्र में रखे जाते हैं।
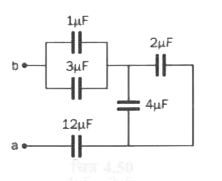
View Solutionचित्र 4.50 में दिखाए परिपथ की तुल्य धारिता ज्ञात करें।
(b ) जब a और b के बीच विभवान्तर 100 V हो , तो 12μF पर संचित हुआ आवेश निकालें।
View Solutionएक वृत्ताकार तार की कुण्डली में 100 फेरे है जिनमें से प्रत्येक का व्यासार्ध 8.0 cm है। इसमें 0.40 A धारा बढ़ती है। कुण्डली के केंद्र पर चुम्बकीय क्षेत्र B का परिमाणक्या है?
View Solutionएक परमाणु में दो इलेक्ट्रॉन , नाभिक के गिर्द R और 4R व्यासार्धों वाली वृत्ताकार कक्षाओं में घूमते हैं। और चक्कर पूरा करने के लिए उनके द्वारा लिए गए समयों का अनुपात ................ है।
View Solutionचार बिंदु आवेश qA=2μC,qB=−5μC,qc=2μC तथा qD=−5μC,10cm भुजा के किसी वर्ग ABCD के शीर्षो पर स्थित है । वर्ग के केंद्र पर रखे 1μC आवेश पर लगने वाला बल कितना है ?
View Solutionकिसी बिंदु आवेश के कारण उस बिंदु को केंद्र मानकर खींचे गए 10cm त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स −1.0×103Nm2/C त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स। (a) यदि गॉऊसीय पृष्ठ की त्रिज्या दो गुनी कर दी जाए तो पृष्ठ से कितना फ्लक्स गुजरेंगा ? (b) बिंदु आवेश का मान क्या है।
View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
View Solutionयदि दो वृतो की त्रिज्याएँ क्रमशः r1 व r2 है और वे एक - दूसरे को बाह्यतः स्पर्शः करते हो , तो -
View Solutionदो विधुतरूधर ताँबे के समरूप आवेशित गोलों A और B में क्रमश: qA और qB आवेश है। उसी साइज का तीसरा अनावेशित गोला C पहले गोले A के संपर्क में रखा जाता है। तथा उसके बाद गोले B के संपर्क में रखा जाता है। अंत में दोनों से दूर कर दिया जाता है। A और B में नए आवेश क्या होंगे ?
View Solutionआवेश || आवेश के प्रकार || आवेश के गुण
View Solutionएक धातु के बेलन को, जिसका व्यास 8 से.मी. और ऊँचाई 90 से. मी. है, गलाकर 12 से. मी. व्यास वाले कितने गोले बनाए जा सकते हैं ?
View SolutionR1 एवं R2 त्रिज्या के दो गोले, जिन पर आवेश क्रमशः Q1 और Q2 है, परस्पर संबंधित किये गये हैं, तब निकाय की ऊर्जा में
View Solutionआवेश के विशिष्ट गुण|आवेश एक अदिश राशि है|आवेश सदैव द्रव्यमान के साथ सम्बन्ध होता है|महतवपूर्ण बिंदु|आवेश का स्थानांतरण|आवेश का क्वांटिकरण|आवेश संरक्षित है|OMR|Summary
View Solutionगतिमान आवेश ओर चुम्बकत्व
View Solutionआवेश व उसके प्रकार#!# आवेश के गुणधर्म और उस पर आधारित प्रशन #!# आवेश को उत्पन करने की विधिया
View Solution
