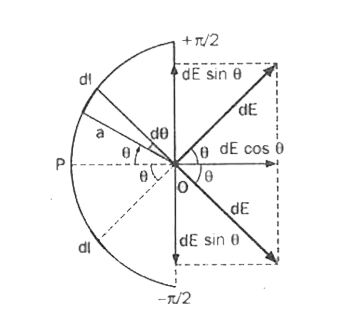
a व्यासार्ध की एक अर्द्धवृत्ताकार चाप , एकसमान रूप से आवेशित की जाती है। प्रति यूनिट लम्बाई आवेश , है। केंद्र पर वैधुत क्षेत्र है
The correct Answer is:C
चाप के dl लम्बाई के एक अंश , जिस पर आवेश dq है के कारण केंद्र O पर वैधुत तीव्रता [ चित्र I.62 ]
सामिमित से
क्योंकि P से ऊपर हर अंश के संगत एक अंश इसके नीचे भी है , इसलिए वाले सारे घटक , एक ही दिशा में होने के कारण एक दूसरे से जुड़ जाते हैं जबकि वाले घटक , विपरीत दिशाओं में होने के कारण एक दूसरे को निरस्त कर देते है )
इस प्रकार
Topper's Solved these Questions
- धारिता और परावैधुत पदार्थ BOOK - GRB PUBLICATION HINDICHAPTER - धारिता और परावैधुत पदार्थ EXERCISE - प्रतियोगिता समाग्री (बहुविकल्पीय प्रश्न : एक या एक से अधिक सही विकल्प
35 Videos
- धारिता और परावैधुत पदार्थ BOOK - GRB PUBLICATION HINDICHAPTER - धारिता और परावैधुत पदार्थ EXERCISE - प्रतियोगिता समाग्री (बहुविकल्पीय प्रश्न : एक या एक से अधिक सही विकल्प (कॉलम मिलाना)
4 Videos
- धारिता और परावैधुत पदार्थ BOOK - GRB PUBLICATION HINDICHAPTER - धारिता और परावैधुत पदार्थ EXERCISE - NCERT पाठ्यपुस्तक अभ्यास : उत्तरों सहित
33 Videos
- धारा के चुम्बकीय प्रभावBOOK - GRB PUBLICATION HINDICHAPTER - धारा के चुम्बकीय प्रभावEXERCISE - NCERT पाठ्यपुस्तक अभ्यासः उत्तरों सहित
14 Videos
- नाभिक BOOK - GRB PUBLICATION HINDICHAPTER - नाभिक EXERCISE - प्रतियोगिता सामग्री (रिक्त स्थान भरना )
25 Videos
Similar Questions
एक प्रोटॉन और एक इलेक्ट्रॉन , एकसमान वैधुत क्षेत्र में रखे जाते हैं।
View Solutionकॉलम - I में कुछ स्थितियाँ दी गई हैं जिनमें R प्रतिरोध का एक सीधा धातु का तार प्रयुक्त होता है और कॉलम - II में कुछ परिणामी प्रभाव दिए गए हैं। कॉलम - I की प्रविष्टियों को कॉलम - II की प्रविष्टियों से मिलाएँ।
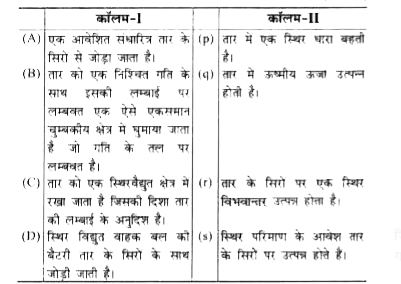
View Solutionदो आवेश 5×10−8C और −3×10−8C एक दूसरे से 16cm दूर हैं इन दोनों आवेशों को जोड़ने वाली रेखा पर किस -किस बिन्दु पर वैधुत विभव शून्य है ? अनन्त पर विभव शून्य लें।
View Solutionएक वृत्ताकार तार की कुण्डली में 100 फेरे है जिनमें से प्रत्येक का व्यासार्ध 8.0 cm है। इसमें 0.40 A धारा बढ़ती है। कुण्डली के केंद्र पर चुम्बकीय क्षेत्र B का परिमाणक्या है?
View Solutionएक परमाणु में दो इलेक्ट्रॉन , नाभिक के गिर्द R और 4R व्यासार्धों वाली वृत्ताकार कक्षाओं में घूमते हैं। और चक्कर पूरा करने के लिए उनके द्वारा लिए गए समयों का अनुपात ................ है।
View Solutionएक द्विआधारी संख्या (cdccddcccddd)2 से निरूपित की जाती है, जहाँ c>d है । इसका दशमलव तुल्य क्या है ?
View Solutionयदि एक दीर्घवृत्त जिसका केंद्र मूलबिंदु पर है, के दीर्घ कक्ष तथा लघु कक्ष कि लम्बाइयों का अंतर 10 है तथा एक नाभिकेन्द्र (0,5√3) पर है, तो इसके नाभिलम्ब की लम्बाई है
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionयदि एक अतिपरवलय के संयुग्मी अक्ष की लम्बाई 5 है तथा इसकी नाभिको के बीच की दुरी 13 है, तो इस अतिपरवलय की उत्केंद्रता है
View Solutionयदि एक दीर्घवृत्त की दीर्घ अक्ष की लम्बाई, उसके लघु अक्ष की लम्बाई की तिगुनी है, तो उसकी उत्केन्द्रता होगी
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solutionकिसी वृत्त में एक चाप केन्द्र पर 45∘का कोण बनाता है। यदि चाप की लम्बाई 11 सेमी है तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionएक घन के विकर्ण की लम्बाई 12√3 सेमी है। घन के कोर की लम्बाई .............होगी।
View Solutionयदि वृत्त के केंद्र से 3 सेमी. की दूरी पर स्थित जीवा की लम्बाई 8 सेमी. है, तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionएक समान चुम्बकीय क्षेत्र में गतिमान आवेश पर बल | संयुक्त विद्युत चुम्बकीय क्षेत्र में आवेशित कण की गति
View Solutionएकसमान चुम्बकीय क्षेत्र में आवेश की गति
View Solution
