Two blocks A and B of masses in and 2m respectively placed on a smooth floor are connected by a spring. A third body C of mass m moves with velocity v0 along the line joining A and B and collides elastically with A. At a certain instant of time after collision it is found that the instantaneous velocities of A and B are same then:
mv20x20
mv02x0
2mv0x0
23m(v0x0)2
The correct Answer is:D
Initial momentum of the system block (c )=mv0 .After striking with A,the block C comes to rest and now both block A and B moves with velocity v when compression in spring is xo.
By the law of conservation of linear momentum
mv0=(m+2m)v⇒v=v03
By the law of conservation of linear momentum
mv0=(m+2m)v⇒v=v03
By the law of conservaion of energy K.E. of block C=K.E. of system
12mv20=12(3m)(v03)2+12kx20
⇒12mv20−16mv20+12kx20
⇒12kx20−12mv20−16mv20=mv203
∴k=23m(v0x0)2
Topper's Solved these Questions
- CONCEPT BUILDERBOOK - DISHA PUBLICATIONCHAPTER - CONCEPT BUILDEREXERCISE - Exercise-1 Concept Builder (topic 4:Collisions)
1 Videos
- COMMUNICATION SYSTEM BOOK - DISHA PUBLICATIONCHAPTER - COMMUNICATION SYSTEM EXERCISE - EXERCISE-2 : Concept Applicator
30 Videos
- CURRENT ELECTRICITYBOOK - DISHA PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-2 Concept Applicator
23 Videos
Similar Questions
Two bodies A and B of masses m and 2 m respectively are placed on a smooth floor. They are connected by a spring. A third body C of mass m moves with velocity v0 along the line joining A and B and collides elastically with A as shown in Fig.
At a certain instant of time t0 after collision, it is found that the instantaneous velocities of A and B are the same. Further at this instant the compression of the spring is found to be x0. Determine (i) the common velocity of A and B at time t0, and (ii) the spring constant.
View SolutionTwo blocks A and B of masses m and 2m respectively are placed on a smooth floor. They are connected by a spring. A third block C of mass m moves with a velocity v0 along the line joing A and B and collides elastically with A, as shown in figure. At a certain instant of time t0 after collision, it is found that the instantaneous velocities of A and B are the same. Further, at this instant the compression of the spring is found to be x0. Determine (i) the common velocity of A and B at time t0, and (ii) the spring constant.
View Solution
Knowledge Check
Two identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
Av√m2kBv√v2kC√mvkDmv2kA block C of mass m is moving with velocity v0 and collides elastically with block A of mass m and connect to another block B of mass 2m through spring constant k. What is k if x0 is compression of spring when velocity of A and B is same ?
Amv20x20Bmv202x20C32mv20x20D23mv20x20A block C of mass m is moving with velocity v0 and collides elastically with block A of mass m and connect to another block B of mass 2m through spring constant k. What is k if x0 is compression of spring when velocity of A and B is same ?
Amv20x20Bmv202x20C32mv20x20D23mv20x20
Two bodies A and B of masses m and 2m respectively are placed on a smooth floor. They are connected by a light spring of stiffness k.
A third body C of mass m moves with velocity v0 along the line joining A and B and collides elastically with A. If lo be the natural length of the spring then find the minimum separation between the blocks.
View SolutionTwo identical blocks A and B each of mass m resting on the smooth horizontal floor are connected by a light spring of natural length L and spring constant K. A third block Cof mass m moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
View SolutionTwo blocks A and B of masses m and 2m are connected by a massless spring of natural length L and spring constant k. The blocks are intially resting on a smooth horizontal floor with the spring at its natural length , as shown . A third identical block C of mass m moves on the floor with a speed v0 along the line joining A and B and collides elastically with A. FInd (a) the velocity of c.m. of system (blockA+B+spring) and (b) the minimum compression of spring.
View Solution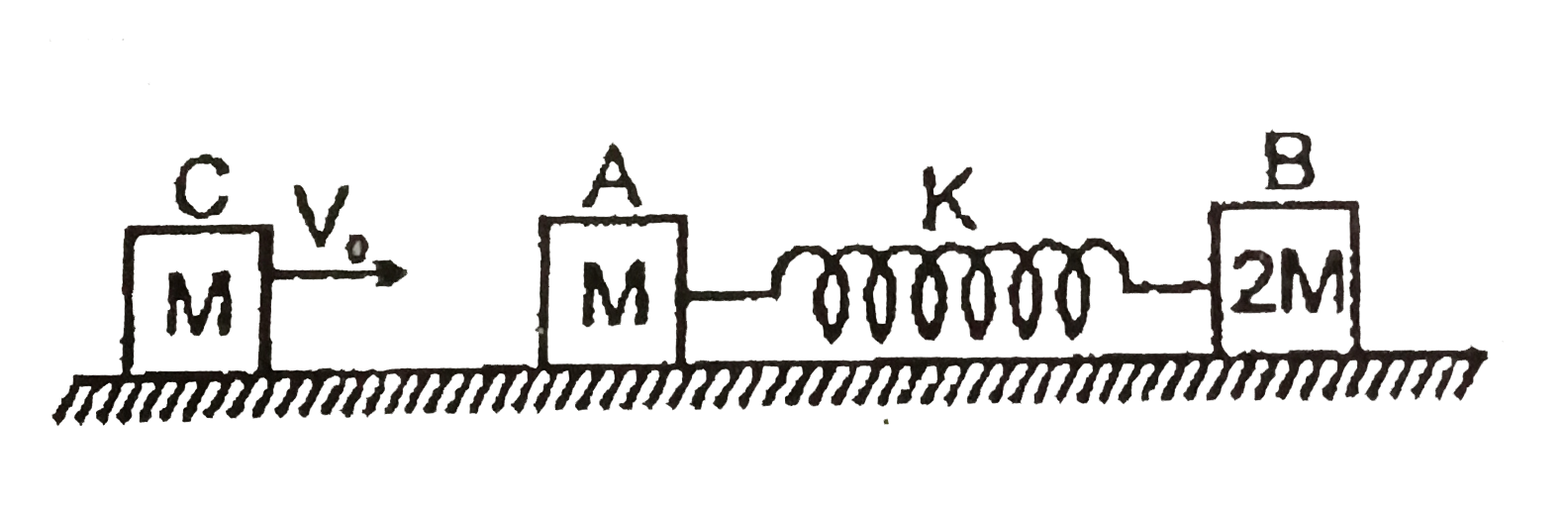
Block C of mass M is moving with velocity V0 and collides elastically with block A of mass M and connected to another block B of mass 2M through a spring of spring constant K. What is K if X0 is the compression of spring when velocity of A and B is same
View SolutionA body of mass M moves with velocity v and collides elasticity with another body of mass m(M>>m) at rest , then the velocity of the body of mass m is
View Solution