During charging a capacitor variation of potential V of the capacitor with time t is shown as




The correct Answer is:A
To solve the problem regarding the variation of potential V of a capacitor with time t during charging, we can follow these steps:
Step 1: Understand the Charging of a Capacitor
When a capacitor is charged through a resistor, the voltage across the capacitor increases over time according to an exponential function. The relationship can be described by the formula:
V(t)=V0(1−e−tRC)
where:
- V(t) is the potential across the capacitor at time t,
- V0 is the maximum potential (or supply voltage),
- R is the resistance in the circuit,
- C is the capacitance of the capacitor,
- e is the base of the natural logarithm.
Step 2: Identify the Nature of the Graph
From the formula, we can see that as time t increases, the term e−tRC decreases, causing V(t) to approach V0. This means that the graph of V versus t will start at 0 volts when t=0 and will asymptotically approach V0.
Step 3: Determine the Shape of the Curve
The graph of V(t) will be an exponential curve. Initially, it will rise steeply and then gradually level off as it approaches V0. This characteristic shape is typical of exponential growth.
Step 4: Choose the Correct Option
Given the options (A, B, C, D), we need to identify which option represents an exponential growth curve. The correct option will show a curve that starts from the origin and approaches a horizontal line (asymptote) at V0.
Final Conclusion
Based on the analysis, the correct answer is option A, which represents the exponential curve of potential V against time t during the charging of a capacitor.
---
When a capacitor is charged through a resistor, the voltage across the capacitor increases over time according to an exponential function. The relationship can be described by the formula:
- V(t) is the potential across the capacitor at time t,
- V0 is the maximum potential (or supply voltage),
- R is the resistance in the circuit,
- C is the capacitance of the capacitor,
- e is the base of the natural logarithm.
From the formula, we can see that as time t increases, the term e−tRC decreases, causing V(t) to approach V0. This means that the graph of V versus t will start at 0 volts when t=0 and will asymptotically approach V0.
The graph of V(t) will be an exponential curve. Initially, it will rise steeply and then gradually level off as it approaches V0. This characteristic shape is typical of exponential growth.
Given the options (A, B, C, D), we need to identify which option represents an exponential growth curve. The correct option will show a curve that starts from the origin and approaches a horizontal line (asymptote) at V0.
Based on the analysis, the correct answer is option A, which represents the exponential curve of potential V against time t during the charging of a capacitor.
Topper's Solved these Questions
- BOOK - DISHA PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - EXERCISE 2: CONCEPT APPLICATOR24videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - DISHA PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - EXERCISE 2: CONCEPT APPLICATOR24videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - DISHA PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise - 2 : Concept Applicator30videos
ELECTROMAGNETIC WAVES
- BOOK - DISHA PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - EXERCISE-230videos
GRAVITATION
Similar Questions
A battery is used to charge a parallel plate combination of two identical capacitors. If the potential difference across the battery is V and the total charge Q flows through the battery during the charging process then 1) The charge on each capacitor is Q/2 and the potential of each capacitor is V/2 2) The charge on each capacitor is Q and the potential of each capacitor is V 3) The charge on each capacitor is Q/2 and the potential of each capacitor is V 4) The charge on each capacitor is Q and the potential of each capacitor is V/2
View SolutionFind charge on each capacitor and potential difference across each capacitor .
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
During charging of capacitor find time when potential drop across capacitor is equal to potential drop across resistance :-
ARC In3BRC In 32CRC ln2D RC ln2 2 - Question 2 - Select One
A capacitor is connected to a variable source of potential. Current flowing in the circuit and potential across the plates of capacitor at time t are shown in figure.

Capacity of the capacitor isA1 FB2 FC3 FD4 F - Question 3 - Select One
A capacitor is connected to a variable source of potential. Current flowing in the circuit and potential across the plates of capacitor at time t are shown in figure.

At t=2s, energy is stored in the capacitor at a rate ofA50 J/sB100 J/sC150 J/sD200 J/s
A 1.5μF capacitor is charged to 20 V. The charging battery is then disconnected , and a 15 mH coil is connected in series with the capacitor so that LC oscillations occur. Write the equation for variation of charge on capacitor and current in the inductor with time taking the instant at which inductor is connected to the capacitor as t=0.
View SolutionDuring charging of capacitor in the circuit shown,
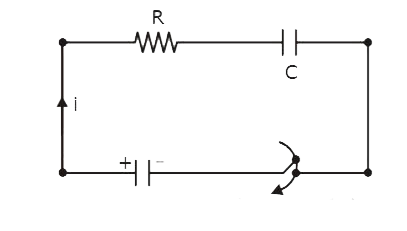
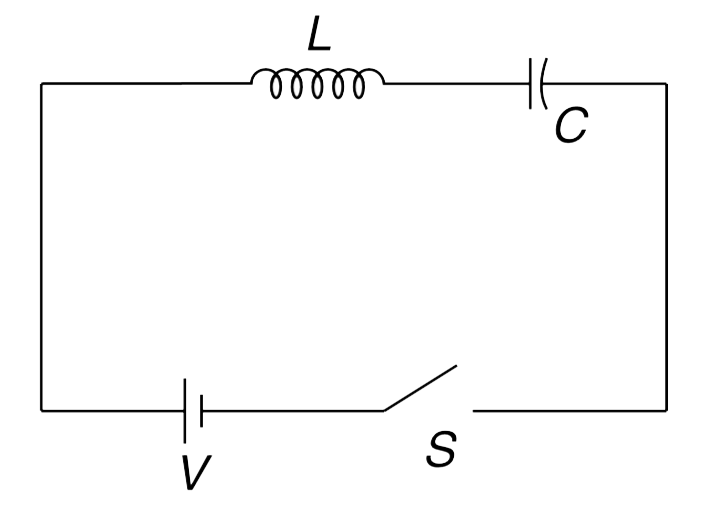
Circuit current versus time graph isView SolutionIn the circuit shown in the figure, switch S is closed at time t=0.
(a) Write current in the circuit and charge on capacitor as a function of time. Draw the graphical plot for the same.
(b) Find maximum charge on the capacitor. What is potential difference across the inductor when charge on the capacitor is maximum?
 View Solution
View SolutionA capacitor of capacitance of 2μF is charged to a potential difference of 200V, after disconnecting from the battery, it is connected in parallel with another uncharged capacitor. The final common potential is 20V then the capacitance of second capacitor is :
View SolutionThe time constant of charging of the capacitor charging of the capacitor shown in figure is
 View Solution
View Solution

