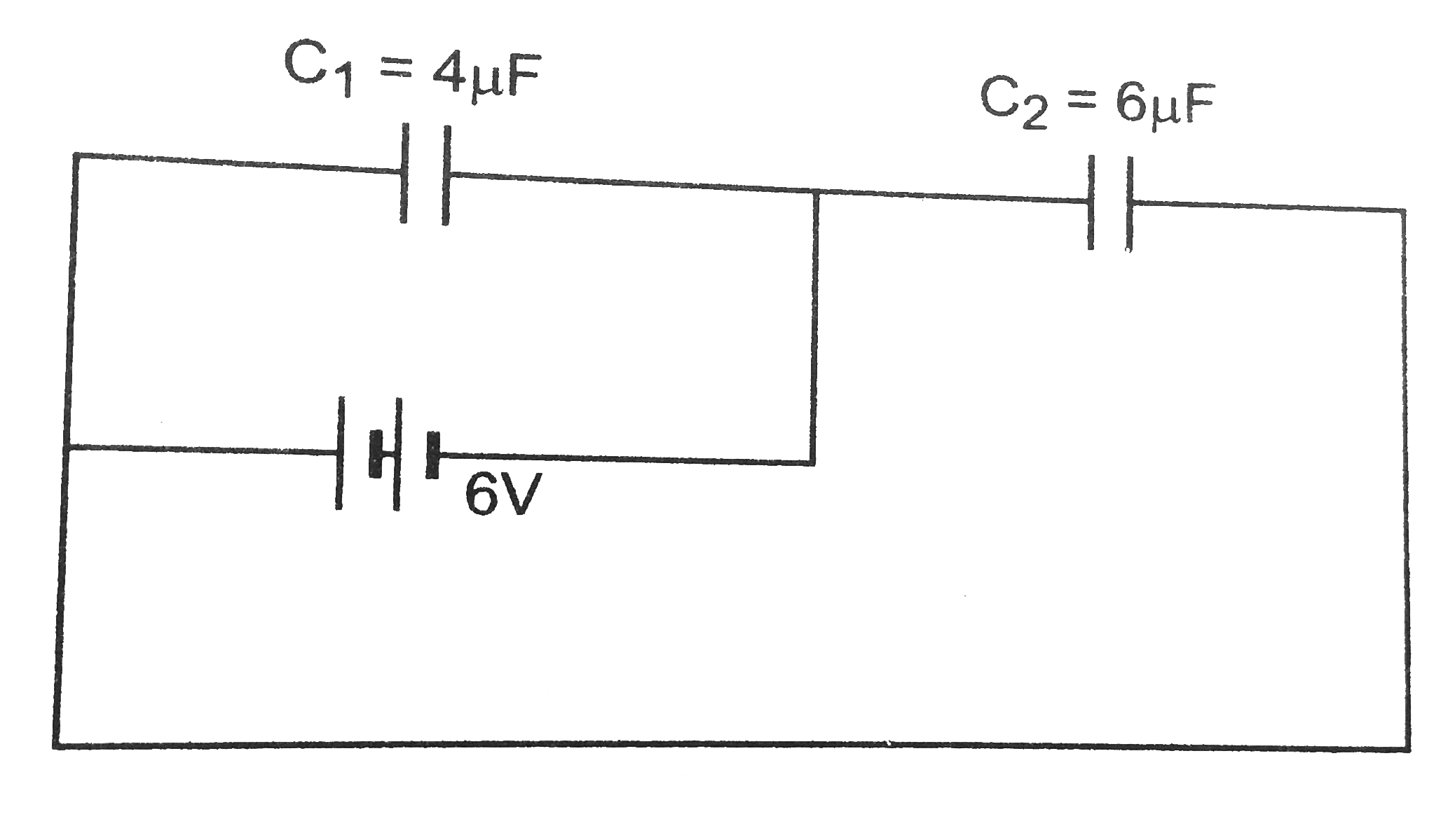
Two capacitors C12μF and C2=6μF are connected in series, then connected in parallel to a third capacitor C3=3μF. This arangement is then connected to a battery of emf 2V as shown in figure. How much energy is lost by the battery in charging the capacitor?

163×10−6J
323×10−6J
11×10−6J
22×10−6J
The correct Answer is:C
We are required to find the energy stored in capacitor combination. Justify we find the net capacitance
Cseries=2×62+6=32μF

Cparallel=32+4=112μF
Total energy stored in capacitors
=12(112)×22=11×10−6J(E=1/2CV2)
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - DISHA PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - EXERCISE 2: CONCEPT APPLICATOR
24 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - DISHA PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - EXERCISE 2: CONCEPT APPLICATOR
24 Videos
- ELECTROMAGNETIC WAVESBOOK - DISHA PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise - 2 : Concept Applicator
30 Videos
- GRAVITATIONBOOK - DISHA PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - EXERCISE-2
30 Videos
Similar Questions
Knowledge Check
Two capacitors C1=2μF and C2=6μF in series, are connected in parallel to a third capacitor C3=4μF. This arrangement is then connected to a battery of e.m.f =2V, as shown in the figure. How much energy is lost by the battery in charging the capacitors
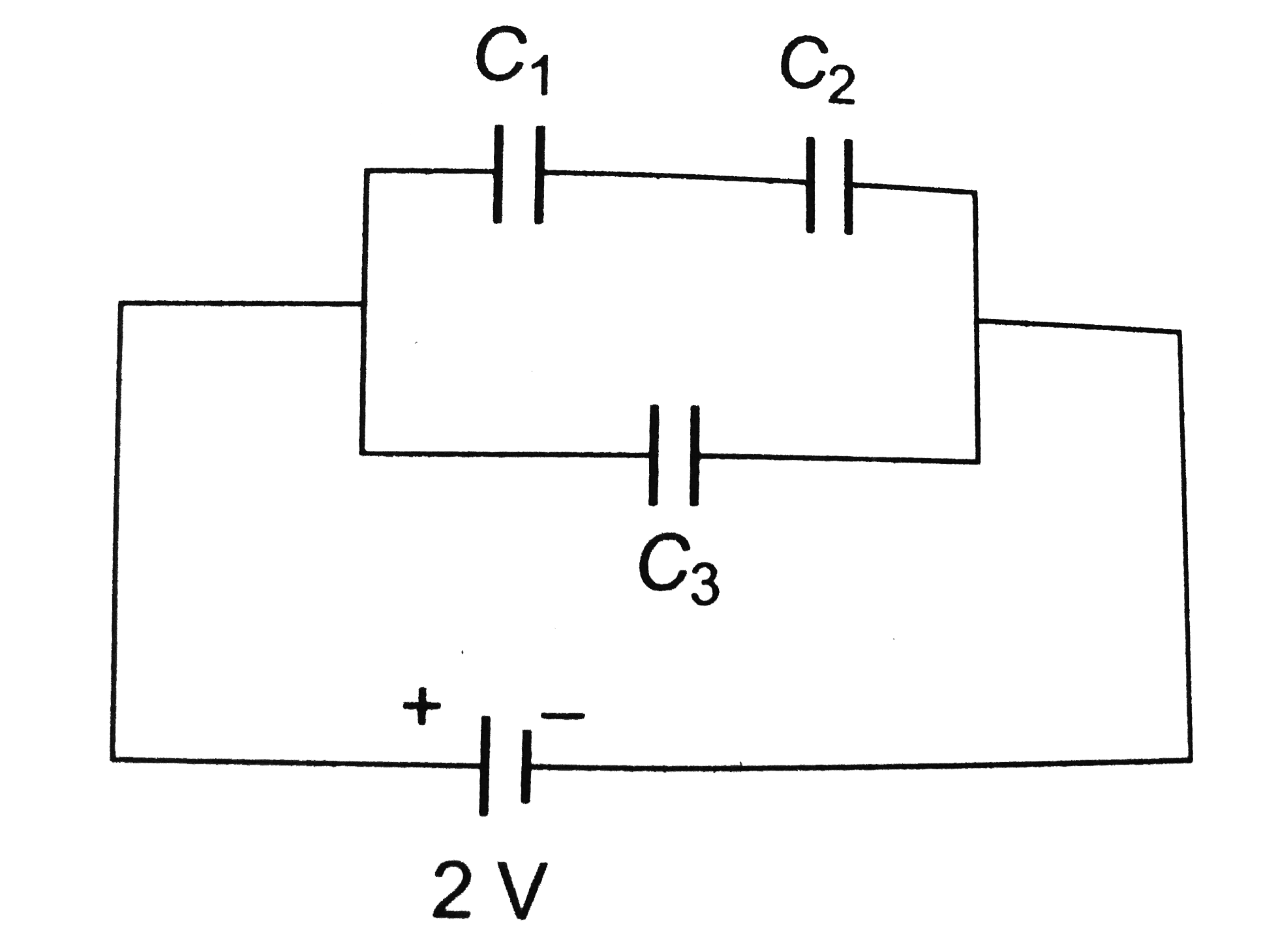 A22×10−6JB11×10−6JC(323)×10−6JD(163)×10−6J
A22×10−6JB11×10−6JC(323)×10−6JD(163)×10−6JTwo capacitors C1=3μF and C2=6μF in series, are connected in parallel to a third capacitor C3=4μF. This arrangement is then connected to a battery of e.m.f., =30V, as shown. The energy lost by the battery in charging the capacitors
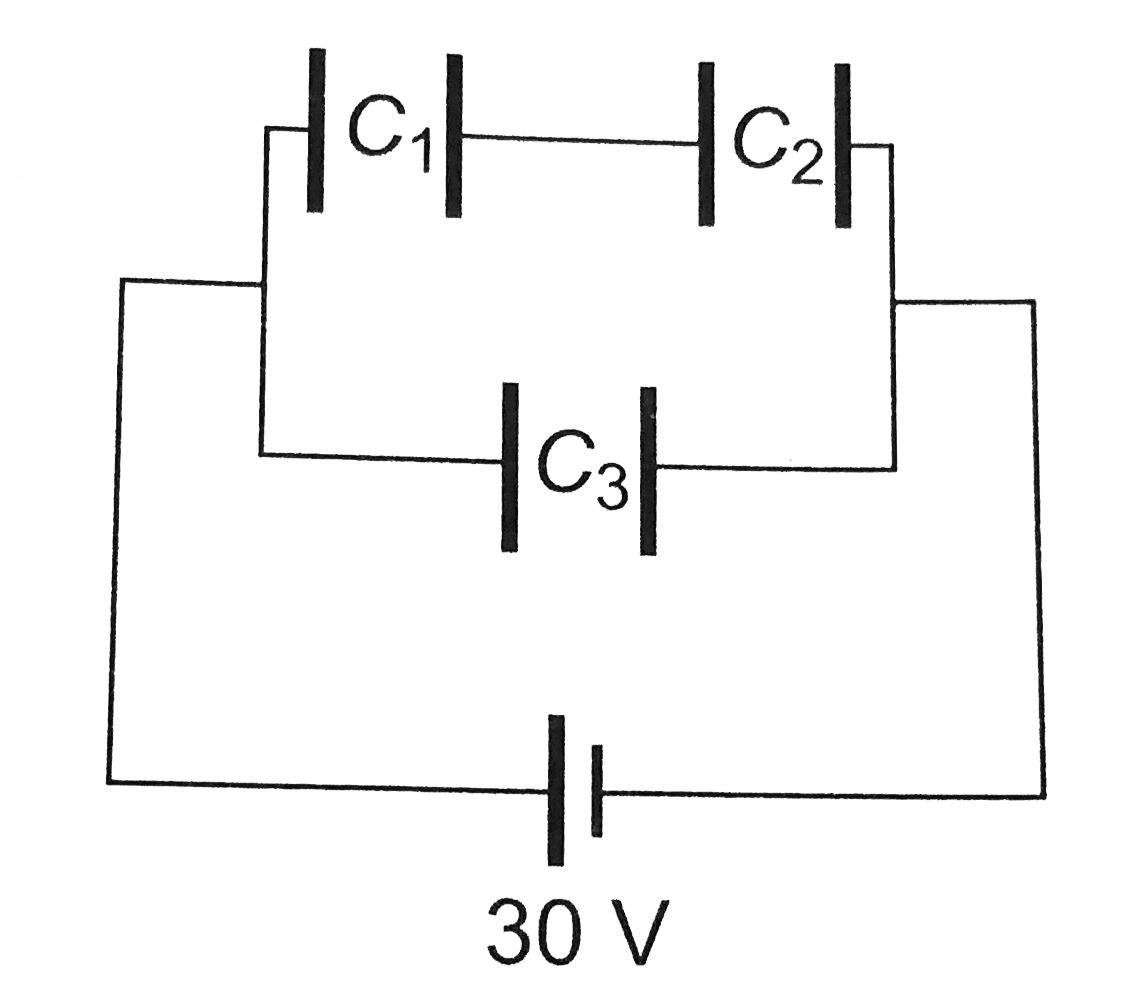 A900μJB1800μJC2700μJD3600μJ
A900μJB1800μJC2700μJD3600μJTwo capacitors 2μF and 4μF are connected in parallel. A third capacitor of 6μFis connected in series. The combination is then connected across a 12V battery. The voltage across 2μF capacitor is:
A2VB6VC8VD1V
Two capacitors of 10μF and 20μF are connected in series with a 30V battery. The charge on the capacitors will be, respectively
View SolutionThree capacitors of 2.0,3.0 and 6.0μF are connected in series to a 10V source. The charge on the 3.0μF capacitor is
View SolutionTwo capacitrors of 2μFand4μF are connected in parallel. A third capacitor of 6μF is connected in series. The combaination is connected across a 12 V battery. The voltage across 2μF capacitor is
View SolutionTwo capacitrors of 2μFand4μF are connected in parallel. A third capacitor of 6μF is connected in series. The combaination is connected across a 12 V battery. The voltage across 2μF capacitor is
View SolutionTwo capacitors 2μFand4μF are connected in parallel. A third capacitor of 6μF capacity is connected in series. The combination is connected across a 12 V battery. The voltage across a 2μF capacitor is

View Solution