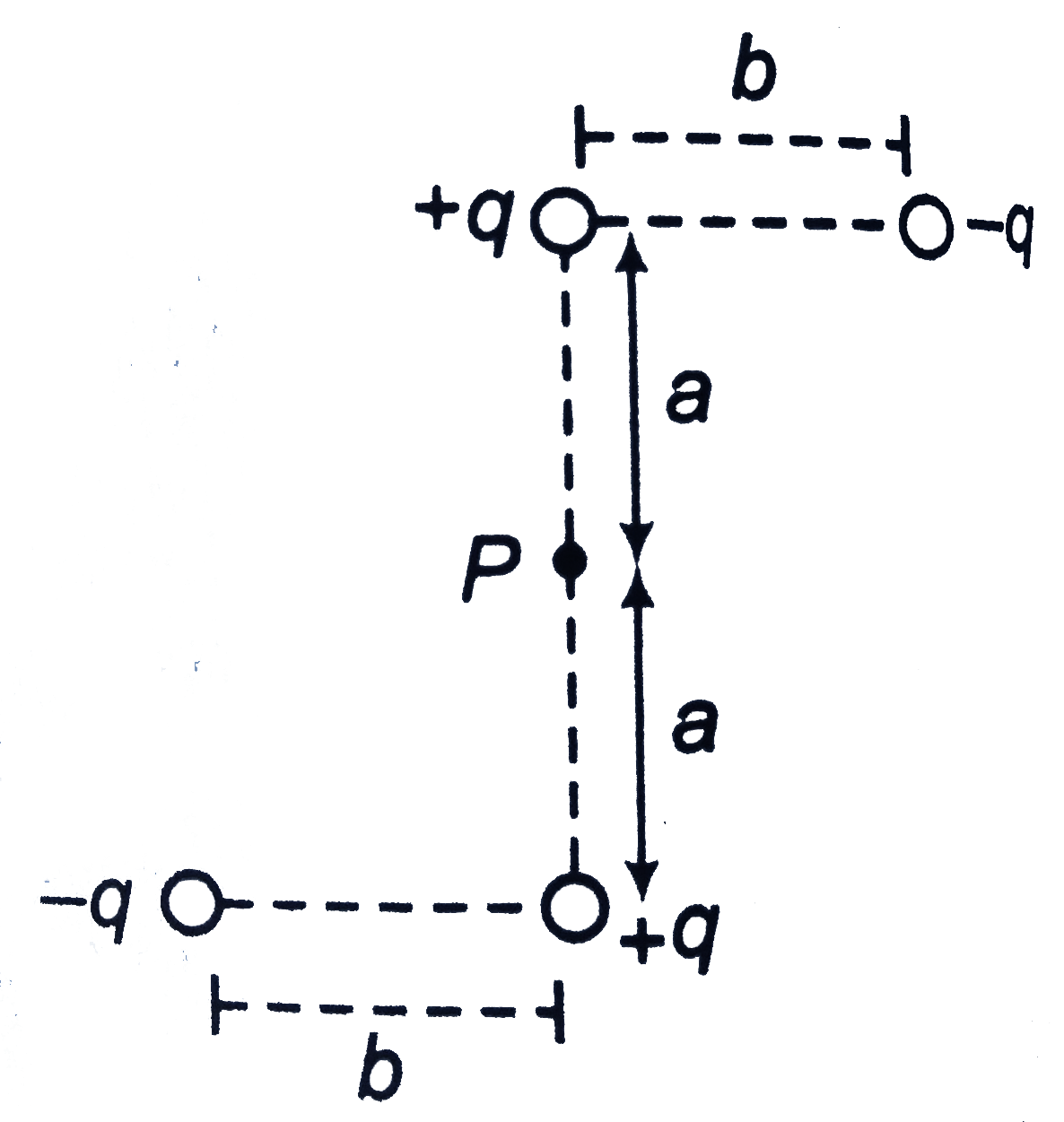
A plastic disc is charged on one side with a uniform surface charge density σ and then three quadrant of the disk are removed. The remaining quadrant is shown in figure.
with V=0 at infinity the potential due to the remaining quadrant at point P is

σ2ε0[(r2+R)1/2−r]
σ2ε0[R−r]
σ8ε0[(r2+R2)1/2−r]
None of these
The correct Answer is:C
The potential at P due to whole disc is
V=σ2ε0[√R2+r2−r]
Now potential due to quarter disc
V=V4=σ8ε0[√R2+r2−r]
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - DISHA PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - EXERCISE -1: CONCEPT BUILDER
58 Videos
- ELECTROMAGNETIC WAVESBOOK - DISHA PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise - 2 : Concept Applicator
30 Videos
- GRAVITATIONBOOK - DISHA PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - EXERCISE-2
30 Videos
Similar Questions
Knowledge Check
A large plate with uniform surface charge density σ is moving with constant speed v as shown in the figure. The magnetic field at a small distance from plate is
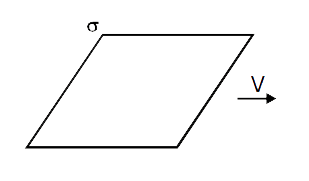 Aμ0σv in magnitudeBμ0σv2 in magnitudeCperpendicular to plateDparallel to plate
Aμ0σv in magnitudeBμ0σv2 in magnitudeCperpendicular to plateDparallel to plateA non-conducting semi circular disc (as shown in figure) has a uniform surface charge density σ. The ratio of electric field to electric potential at the centre of the disc will be
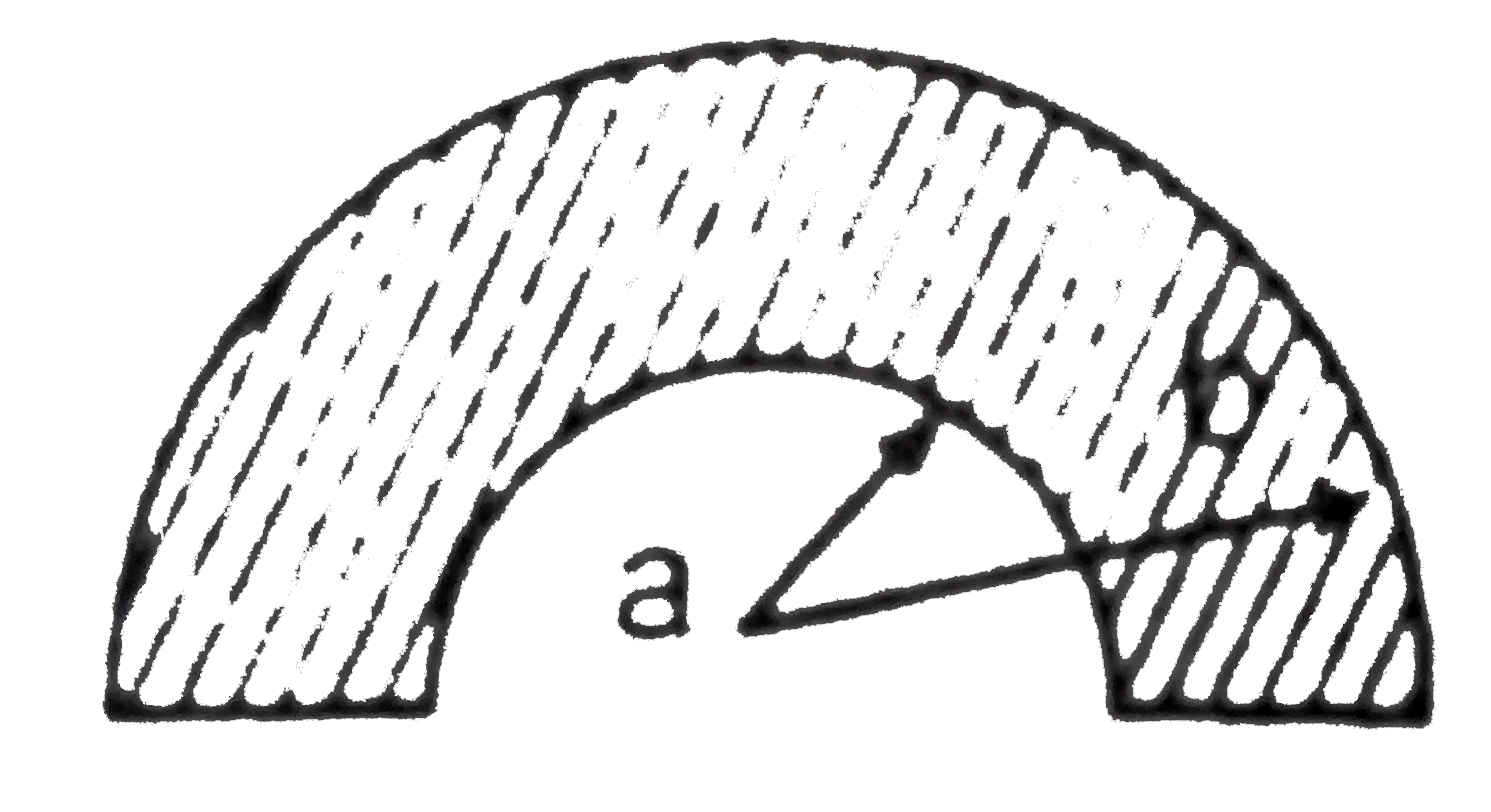 A1πlnb/a(b−a)B2πC1πln(b/a)2(b−a)Dπ(b−a)2ln(b/a)
A1πlnb/a(b−a)B2πC1πln(b/a)2(b−a)Dπ(b−a)2ln(b/a)A small section of area ΔA is removed from a uniform spherical shell with surface mass density σ and radius R as shown in the figure . Find the magnitude of gravitational field intensity at point P due to the remaining mass .
 A4σΔAG9R2B4σΔAGR2CσΔAGR2Dzero
A4σΔAG9R2B4σΔAGR2CσΔAGR2Dzero
A non-conducting semi circular disc (as shown in figure) has a uniform surface charge density σ. The ratio of electric field to electric potential at the centre of the disc will be

View SolutionA small section of area ΔA is removed from a uniform spherical shell with surface mass density σ and radius R as shown in the figure . Find the magnitude of gravitational field intensity at point P due to the remaining mass .

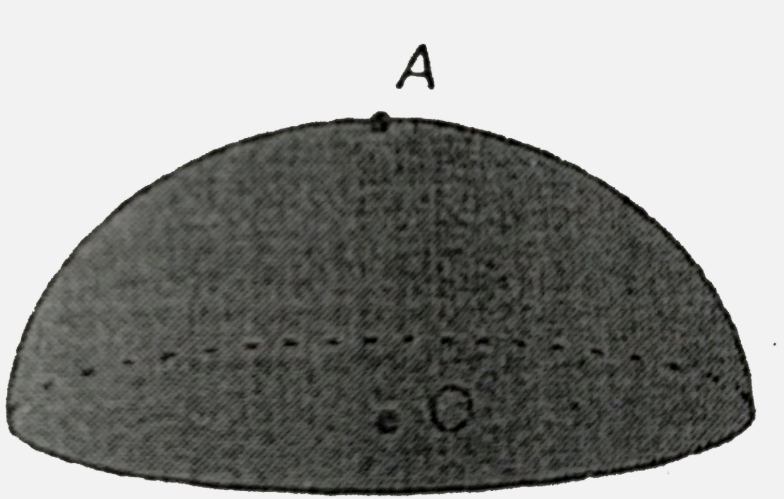
View SolutionA hemispherical bowl of radius R carries a uniform surface charge density σ. Find the potential at the topmost point A, taking potential at infinity to be zero.
View SolutionAn annular disc of inner radius a and outer radius '2a' is uniformly charged with uniform surface charge density σ. Find the potential at a distance 'a' from the centre at a point 'P' lying on the axis.
View SolutionThree large parallel plates have unifrom surface charge densities as shown in the figure. What is the electric field at P
 .
.
View Solution