When a thin transparent plate of thickness t and refractive index is placed in the path of one the two interfering waves of light, then the path difference changes by
The correct Answer is:B
To solve the problem of how the path difference changes when a thin transparent plate of thickness t and refractive index μ is placed in the path of one of the two interfering waves of light, we can follow these steps:
1. Understanding the Optical Path Length:
- The optical path length (OPL) is defined as the product of the physical path length and the refractive index of the medium through which light travels.
- For a medium with thickness t and refractive index μ, the optical path length is given by:
OPL=μ⋅t
2. Identifying the Change in Path:
- When there is no plate, the light travels a distance t in air (or vacuum), which has a refractive index of approximately 1. Thus, the optical path length without the plate is simply:
OPLwithout plate=t
3. Calculating the Change in Optical Path Length:
- When the thin transparent plate is introduced, the optical path length changes to μ⋅t.
- The change in optical path length (ΔOPL) due to the introduction of the plate can be calculated as:
ΔOPL=OPLwith plate−OPLwithout plate=μt−t
4. Factoring the Change:
- We can factor out t from the equation:
ΔOPL=t(μ−1)
5. Conclusion:
- Thus, the change in path difference when a thin transparent plate of thickness t and refractive index μ is placed in the path of one of the interfering waves of light is:
ΔOPL=t(μ−1)
Final Answer:
The path difference changes by t(μ−1).
---
- The optical path length (OPL) is defined as the product of the physical path length and the refractive index of the medium through which light travels.
- For a medium with thickness t and refractive index μ, the optical path length is given by:
OPL=μ⋅t
- When there is no plate, the light travels a distance t in air (or vacuum), which has a refractive index of approximately 1. Thus, the optical path length without the plate is simply:
OPLwithout plate=t
- When the thin transparent plate is introduced, the optical path length changes to μ⋅t.
- The change in optical path length (ΔOPL) due to the introduction of the plate can be calculated as:
ΔOPL=OPLwith plate−OPLwithout plate=μt−t
- We can factor out t from the equation:
ΔOPL=t(μ−1)
- Thus, the change in path difference when a thin transparent plate of thickness t and refractive index μ is placed in the path of one of the interfering waves of light is:
ΔOPL=t(μ−1)
The path difference changes by t(μ−1).
Topper's Solved these Questions
- WAVE OPTICSBook:DISHA PUBLICATIONChapter:WAVE OPTICSExercise:EXERCISE-2 : CONCEPT APPLICATOR
Explore 30 Videos
- WAVE OPTICSBook:DISHA PUBLICATIONChapter:WAVE OPTICSExercise:EXERCISE-2 : CONCEPT APPLICATOR
Explore 30 Videos
- THERMODYNAMICS Book:DISHA PUBLICATIONChapter:THERMODYNAMICS Exercise:EXERCISE -2 : CONCEPT APPLICATOR
Explore 29 Videos
- WAVESBook:DISHA PUBLICATIONChapter:WAVESExercise:EXERCISE -2 CONCEPT APPLICATOR
Explore 30 Videos
Similar Questions
In YDSE, when a glass plate of refractive 1.5 of thickness t is placed in the path of one of the interfering beams of wavelength λ, intensity at the position where central maximum occurred previously remain unchanged. If the minimum thicknes of the glass plate is kλ. Find the value of k........
View SolutionIn Young's double slit experiment the two slits are illuminated with light of wavelength λ .The thickness of a film of refractive index 1.4 to be introduced in the path of one of the interfering beams so that the central image shifts by one fringe width is
View Solution
Knowledge Check
In Young's double slit experiment, using monochromatic light, the fringe patternn shifts by a certain distance on the screen, when a transparent sheet of thickness 't' and refractive index μ is introduced in the path of one of the interfering waves. the sheet is then removed and the distance between the screen and the slits is doubled. it is found that the distance between the successive maxima (or minima) now is the samme as the observed fringe shift when the sheet was introduced. what is the wavelength of light used?
Aλ=(μ−1)tBλ=(μ−1)t2Cλ=(μ+1)tDλ=(μ+1)t2When a thin metal plate is placed in the path of one of the interfering beams of light
AFringe width increasesBFringes disappearCFringes become brighterDFringes becomes blurredIf a thin mica sheet of thickness 't' and refractive index μ is placed in the path of one of the waves producing interference , then the whole interference pattern shifts towards the side of the sheet by a distance
AdD(μ−1)tBDd(μ−1)tCDd(μ−1)tD(μ−1)t
When a transparent parallel plate of uniform thickness t and refractive index μ is interposed normally in the path of a beam of light, the optical path is
View SolutionA YDSE is conducted in water (μ1) as shown in figure. A glass plate of thickness t and refractive index μ2 is placed in the path of S2. The optical path difference at O is
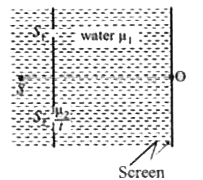
View SolutionA thin perfectly transparent glass sheet of thickness t and refractive index mu is pasted on one of the two identical slits. If the intensity of light at the centre of the screen is I0 in the absence of glass sheet, the intensity at O as a function of thickness of the glass plate is
View SolutionWhen the plastic thin film of refractive index 1.45is placed in the path of one of the interfering waves then the central fringe is displaced through width of five fringes.The thickness of the film will be ,if the wavelength of light is5890Å
View SolutionIf path difference between two interfering waves is zero, then the point will be
View Solution
