If in hydrogen atom, radius of nth Bohr orbit is rn., frequency of revolution of electron in nth orbit is fn choose the correct option.
Both (a) and (b)
The correct Answer is:D
To solve the problem regarding the radius and frequency of the electron in the nth Bohr orbit of a hydrogen atom, we will follow these steps:
Step 1: Understanding the Radius of the nth Bohr Orbit
The radius rn of the nth Bohr orbit is given by the formula:
rn=a0⋅n2
where a0 is the Bohr radius (approximately 0.529 Å for hydrogen), and n is the principal quantum number.
Step 2: Analyzing the Relationship
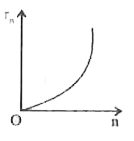
From the formula rn=a0⋅n2, we can see that the radius rn is directly proportional to the square of the quantum number n. Therefore, if we plot rn against n, we will get a parabolic graph.
Step 3: Frequency of Revolution of the Electron
The frequency of revolution fn can be derived from the time period T of one complete revolution:
fn=1T
The time period T can be calculated as the distance traveled in one revolution divided by the speed of the electron. The distance traveled in one revolution is the circumference of the orbit:
T=2πrnv
where v is the speed of the electron.
Step 4: Expressing Speed in Terms of n
The speed v of the electron in the nth orbit can be related to n as:
v∝Zn(for hydrogen, Z=1)
Thus, we can express v as:
v=k⋅1n
where k is a constant.
Step 5: Substituting into the Time Period Formula
Substituting rn and v into the time period formula:
T=2π(a0n2)k⋅1n=2πa0n3k
Thus, the frequency becomes:
fn=k2πa0n3
Step 6: Finding the Ratio of Frequencies
To find the ratio of frequencies fnf1:
fnf1=fnk/(2πa0)=1n3
Step 7: Taking Logarithm
Taking the logarithm of the ratio:
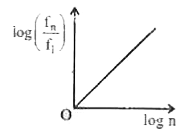
log(fnf1)=−3log(n)
This indicates a linear relationship with a negative slope when plotted.
Conclusion
Based on the analysis:
- The graph of rn vs. n is parabolic.
- The graph of log(fnf1) vs. log(n) is a straight line with a negative slope.
Final Answer
The correct options are:
- A: The graph of rn vs. n is parabolic.
- B: The graph of log(fnf1) vs. log(n) is a straight line with a negative slope.
Thus, the answer is D: Both A and B are correct.
The radius rn of the nth Bohr orbit is given by the formula:
rn=a0⋅n2
where a0 is the Bohr radius (approximately 0.529 Å for hydrogen), and n is the principal quantum number.
From the formula rn=a0⋅n2, we can see that the radius rn is directly proportional to the square of the quantum number n. Therefore, if we plot rn against n, we will get a parabolic graph.
The frequency of revolution fn can be derived from the time period T of one complete revolution:
fn=1T
The time period T can be calculated as the distance traveled in one revolution divided by the speed of the electron. The distance traveled in one revolution is the circumference of the orbit:
T=2πrnv
where v is the speed of the electron.
The speed v of the electron in the nth orbit can be related to n as:
v∝Zn(for hydrogen, Z=1)
Thus, we can express v as:
v=k⋅1n
where k is a constant.
Substituting rn and v into the time period formula:
T=2π(a0n2)k⋅1n=2πa0n3k
Thus, the frequency becomes:
fn=k2πa0n3
To find the ratio of frequencies fnf1:
fnf1=fnk/(2πa0)=1n3
Taking the logarithm of the ratio:
log(fnf1)=−3log(n)
This indicates a linear relationship with a negative slope when plotted.
Based on the analysis:
- The graph of rn vs. n is parabolic.
- The graph of log(fnf1) vs. log(n) is a straight line with a negative slope.
The correct options are:
- A: The graph of rn vs. n is parabolic.
- B: The graph of log(fnf1) vs. log(n) is a straight line with a negative slope.
Topper's Solved these Questions
- BOOK - DISHA PUBLICATIONCHAPTER - ATOMSEXERCISE - EXERCISE-1: CONCEPT BUILDER (TOPICWISE)60videos
ATOMS
- BOOK - DISHA PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - Exercise -2 : Concept Applicator30videos
ALTERNATING CURRENT
- BOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER 29 : (COMMUNICATION SYSTEMS)15videos
CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
If in hydrogen atom, radius of nth Bohr orbit is , nr frequency of revolution of electron in nth orbit is fn choose the correct option
A B
B C
C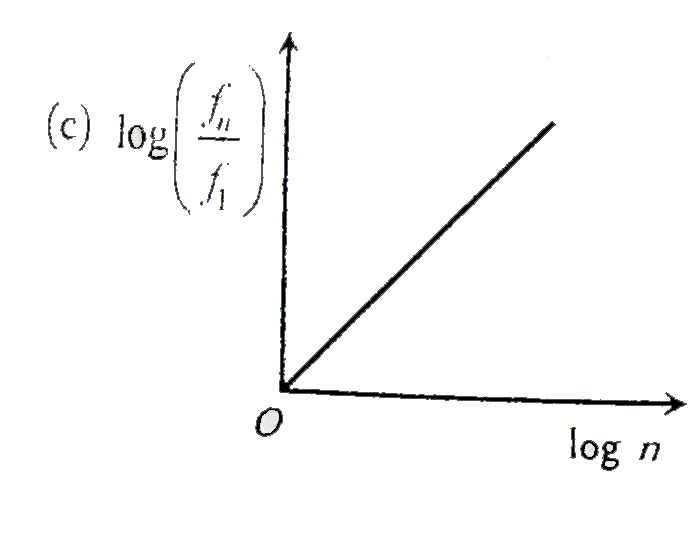 DBoth (a) and (b)
DBoth (a) and (b) - Question 2 - Select One or More
If, in a hydrogen atom, radius of nth Bohr orbit is rn frequency of revolution of electron in nth orbit is fn and area enclosed by the nth orbit is An , then which of the pollowing graphs are correct?
A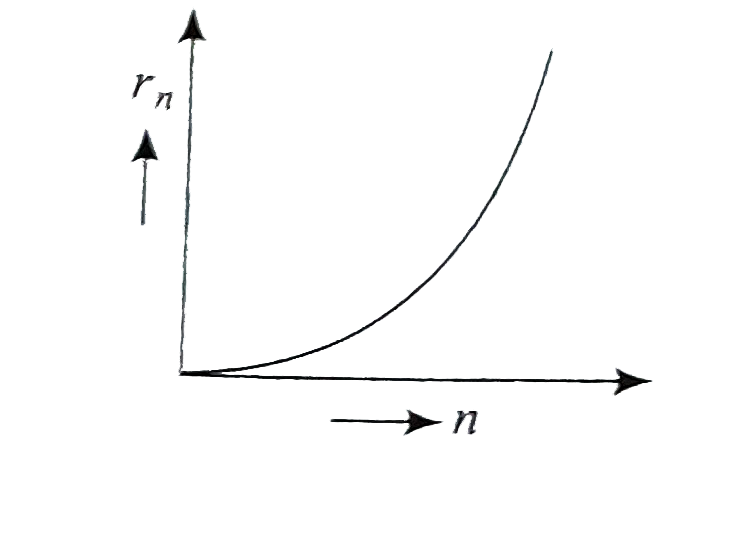 B
B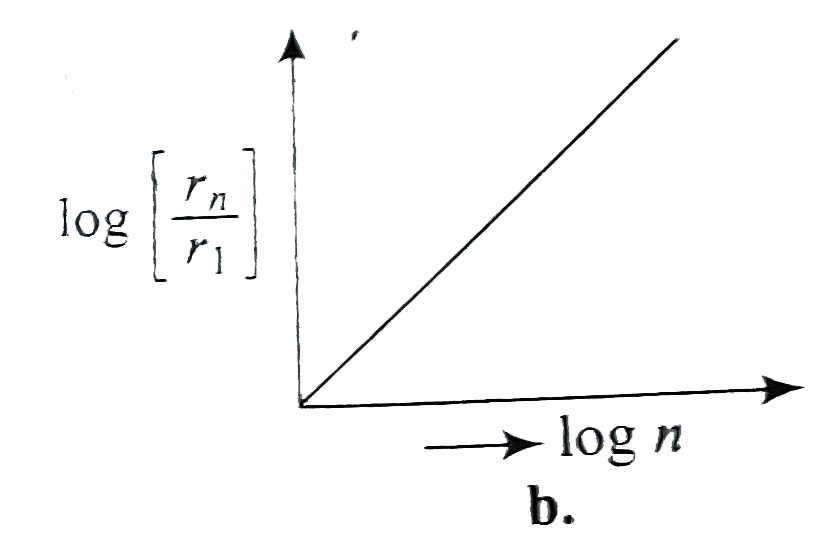 C
C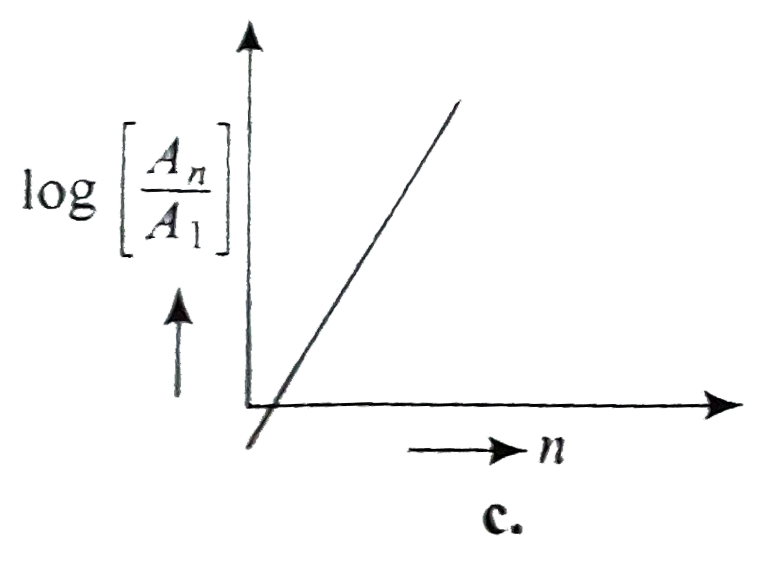 D
D
- Question 3 - Select One
Frequency of revolution of electron in the nth Bohr's orbit is given by
Af=me44∈20n3h3Bf=4∈20n3h3Cf=me44∈20h2Df=me4∈0n
If the frequency of revolution of electron in an orbit H atom is n then the equivalent current is
View SolutionPeriod of revolution of electron in the nth bohr's orbit is given by
View SolutionThe moment of inertia of an electron in nth orbit will be
View SolutionThe angular momentum of electron in nth orbit is given by
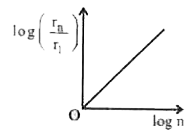
View SolutionIn hydrogen atom, the radius of nth Bohr orbit is Vn. The graph Beetween log.(rnr1) will be
View Solution

