आकृति में एक ही आधार BC पर दो त्रिभुज ABC तथा DBC बने हुए है। यदि AD, BC को O पर प्रतिच्छेद करे तो दर्शाइए कि
ar(ΔABC)ar(ΔDBC)=AODO
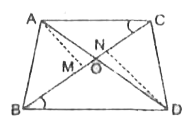
Step by step video & image solution for आकृति में एक ही आधार BC पर दो त्रिभुज ABC तथा DBC बने हुए है। यदि AD, BC को O पर प्रतिच्छेद करे तो दर्शाइए कि (ar(DeltaABC))/(ar(DeltaDBC))=(AO)/(DO) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिभुज BOOK - ALOK BHARTI PUBLICATIONCHAPTER - त्रिभुज EXERCISE - दीर्घ उत्तरीय प्रश्न एवं उत्तर
3 Videos
- त्रिभुज BOOK - ALOK BHARTI PUBLICATIONCHAPTER - त्रिभुज EXERCISE - दीर्घ उत्तरीय प्रश्न एवं उत्तर
3 Videos
- त्रिकोणमितीय अनुपात BOOK - ALOK BHARTI PUBLICATIONCHAPTER - त्रिकोणमितीय अनुपात EXERCISE - प्रश्नावली 8.6
8 Videos
- दो चरों में रैखिक समीकरण BOOK - ALOK BHARTI PUBLICATIONCHAPTER - दो चरों में रैखिक समीकरण EXERCISE - प्रश्नावली 3.5
38 Videos
Similar Questions
सिद्ध करें कि यदि किसी त्रिभुज की एक भुजा के समांतर अन्य दो भुजाओं को काटते हुए कोई रेखा खींचे तो यह त्रिभुज की अन्य दोनों भुजाओं की समान अनुपात में विभाजित करती है।
View Solutionसिद्ध करें कि यदि किसी त्रिभुज की एक भुजा के समांतर अन्य दो भुजाओं को काटते हुए कोई रेखा खींचे तो यह त्रिभुज की अन्य दोनों भुजाओं की समान अनुपात में विभाजित करती है।
View Solution200 मीटर ऊँची एक पहाड़ी की चोटी से एक खंभे के शीर्ष एवं आधार के अवनमन कोण क्रमश : 30∘ एवं 60∘ है। खंभे की ऊँचाई तथा मीनार से उसकी दुरी ज्ञात करे
View Solutionदो संख्याओं का योगफल 15 है। यदि उनके व्युत्क्रम का योगफल हो 310तो वह संख्या ज्ञात करें।
View SolutionIn Fig. 6.44, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that (ar (ABC))/( ar (DBC))= (AO )/( DO )
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionIn the given figure, AB is a diameter, O is the center of the circle and ∠OCB=50∘ then find ∠DBC.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionIn the given figure, ΔABCandΔDBC have the same base BC. If AD and BC intersect at O, prove that ar(ΔABC)ar(ΔDBC)=AODO
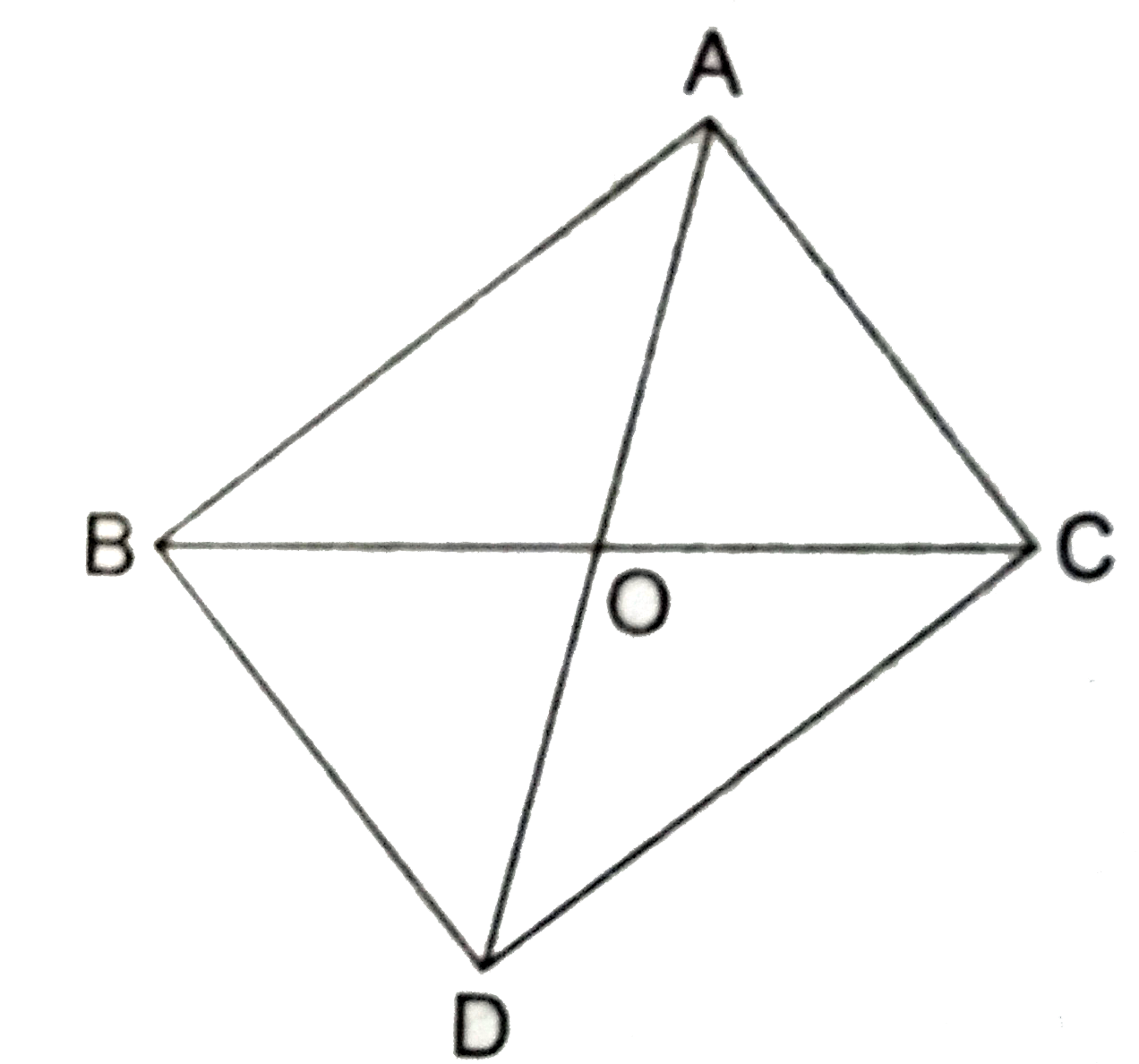
View Solutionआकृति में एक ही आधार BC पर दो त्रिभुज ABC और DBC बने हुए है। यदि AD,BD को O पर प्रतिच्छेद पर तो दर्शाइए कि ar(ΔABC)ar(ΔDBC)=AODO है।
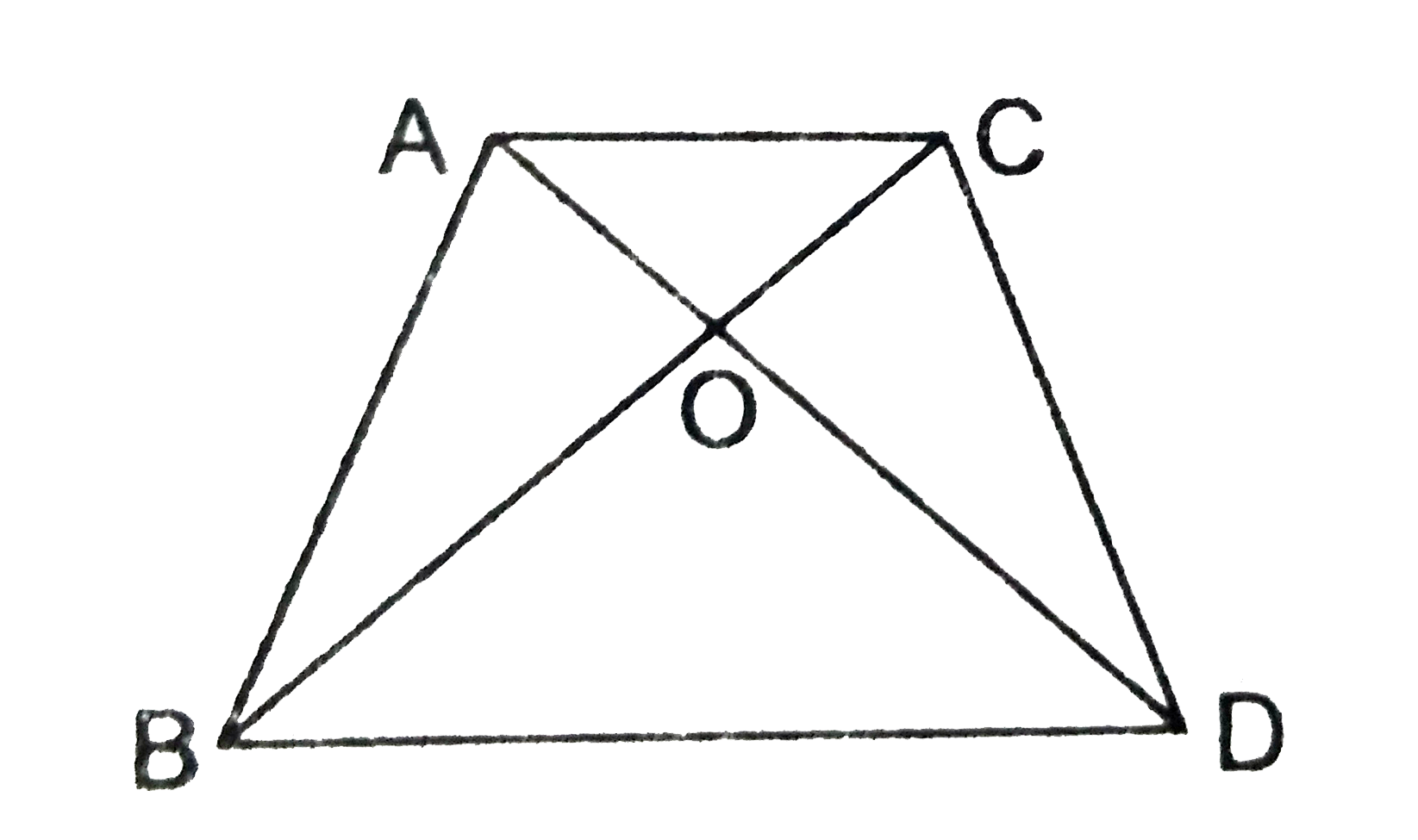
View SolutionIn Fig , ABC and DBC are two triangles on the same base BC. If AD intersects BC,at O , show that ar(ABC)ar(DBC)=AODO
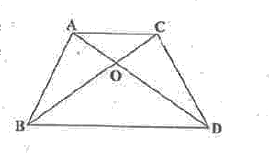
View Solution
