Two particles of masses 1.0 kg and 2.0 kg are placed at a separation of 50 cm. Assuming that the only forces acting on the particles are their mutual gravitation find the initial acceleration of the two particles.
Force exerted by one particle on another is F=Gm1m2r2=6.67×10−11×1×2(0.5)2=5.34×10−10N
acceleration of heavier particle =Fm2=5.3×10−102=2.67×10−10m/s2.
Note : This example shows that gravitational force is quite weak but this is the only force keep binds our solar system and also the universe and also the univers comparising of all galaxies and other interstellar system.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - BOX-13videos
GRAVITATION
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - BOX-212videos
GRAVITATION
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 5 B (Previous Year Questions)9videos
GRAVITATION
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective14videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)48videos
KINEMATICS-2D
Similar Questions
Two particles of mass 200 g each are placed at a separation of 10 cm. Assume that the only forces acting on them are due to their gravitational attraction. Find the acceleration of each when they are allowed to move.
View SolutionTwo particles of masses 1kg and 2kg are placed at a distance of 50cm. Find the initial acceleration of the first particle due to gravitational force.
View Solution
Knowledge Check
- Question 1 - Select One
Two particles of masses 1 kg and 2 kg are placed at a separation of 50 cm find out gravitational force between them
A5.3x10−10NB4.9×10−9NC6.5×10−8ND6.9×x10−7N - Question 2 - Select One
Two particles of masses 1kg and 2kg are located at x=0 and x=3m. Find the position of their centre of mass.
A2m from 1 kgB2m from 2 kgC1m from 1 kgDnone of these - Question 3 - Select One
Three particles, each of the mass m are situated at the vertices of an equilateral triangle of side a. The only forces acting on the particles are their mutual gravitational forces. It is desired that each particle moves in a circle while maintaining the original mutual separation a. Find the initial velocity that should be given to each particle and also the time period of the circular motion. (F=Gm1m2r2)
A2π√a13GmB2π√a23GmC2π√a32GmD2π√a33Gm
Three particles, each of mass m are fixed at the vertices of an equilateral triangle of side length a. The only forces acting on the particles are their mutual gravitational forces. Then answer the following questions.
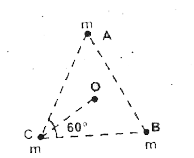
Force acting on particle C, due to particle A and BView SolutionTwo particle of mass 1 kg and 2 kg are located at x = 0 and x = 3 m. Find the position of their centre of mass.
 View Solution
View SolutionThree particles, each of mass m are fixed at the vertices of an equilateral triangle of side length a. The only forces acting on the particles are their mutual gravitational forces. Then answer the following questions.

The gravitational potential at O isView SolutionThree particles, each of mass m, are situated at the situated at the vertices of an equilateral triangle of side 'a'. The only forces acting on the particles are their mutual gravitational forces. It is intended that each particle moves along a circle while maintaining their original separation 'a'. Determine the initial velocity that should be given to each particle and the time period of the circular motion. The resultant force on particle at A due to other two particles is
View SolutionTwo particles of masses 2m and 3m are placed at separation d on a smooth surface. They move towards each other due to mutual attractive force. Find (a) acceleration of c.m. (b) Velocity of c.m. when separation between particles becomes d/3. ( c) At what distance from the initial position of mass 2m, the particles collide.
View Solution

