Two stationary particles of masses M1 and M2 are 'd' distance apart. A third particle lying on the line joining the particles, experiences no resultant gravitational force. What is the distance of this particle from M1 ?
To solve the problem step by step, we will analyze the gravitational forces acting on the third particle and find its distance from mass M1.
Step 1: Understand the Setup
We have two stationary particles with masses M1 and M2 separated by a distance d. A third particle of mass m is placed on the line joining M1 and M2 at a distance x from M1. Therefore, the distance from M2 to the third particle will be d−x.
Hint: Visualize the setup with a diagram to understand the positions of the masses.
Step 2: Write the Gravitational Forces
The gravitational force F13 between M1 and the third particle m is given by:
F13=GM1mx2
The gravitational force F32 between M2 and the third particle m is given by:
F32=GM2m(d−x)2
Hint: Remember that the gravitational force is inversely proportional to the square of the distance between the masses.
Step 3: Set the Forces Equal
Since the third particle experiences no resultant gravitational force, the forces F13 and F32 must be equal:
F13=F32
This leads to:
GM1mx2=GM2m(d−x)2
Hint: You can cancel out the common terms (like G and m) from both sides of the equation.
Step 4: Simplify the Equation
After canceling, we have:
M1x2=M2(d−x)2
Cross-multiplying gives:
M1(d−x)2=M2x2
Hint: This step involves algebraic manipulation; ensure you distribute correctly.
Step 5: Expand and Rearrange
Expanding the left side:
M1(d2−2dx+x2)=M2x2
This simplifies to:
M1d2−2M1dx+M1x2=M2x2
Rearranging gives:
M1d2=(M2−M1)x2+2M1dx
Hint: Keep track of your variables and coefficients while rearranging.
Step 6: Solve for x
Rearranging further leads to:
(M2−M1)x2+2M1dx−M1d2=0
This is a quadratic equation in x. We can solve it using the quadratic formula:
x=−b±√b2−4ac2a
where a=M2−M1, b=2M1d, and c=−M1d2.
Hint: Identify coefficients carefully for the quadratic formula.
Step 7: Final Expression for x
After solving the quadratic equation, we find:
x=d√M1√M1+√M2
Hint: Ensure you check the signs and the physical meaning of the solution.
Conclusion
The distance of the third particle from M1 is given by:
x=d√M1√M1+√M2
We have two stationary particles with masses M1 and M2 separated by a distance d. A third particle of mass m is placed on the line joining M1 and M2 at a distance x from M1. Therefore, the distance from M2 to the third particle will be d−x.
The gravitational force F13 between M1 and the third particle m is given by:
F13=GM1mx2
The gravitational force F32 between M2 and the third particle m is given by:
F32=GM2m(d−x)2
Since the third particle experiences no resultant gravitational force, the forces F13 and F32 must be equal:
F13=F32
This leads to:
GM1mx2=GM2m(d−x)2
After canceling, we have:
M1x2=M2(d−x)2
Cross-multiplying gives:
M1(d−x)2=M2x2
Expanding the left side:
M1(d2−2dx+x2)=M2x2
This simplifies to:
M1d2−2M1dx+M1x2=M2x2
Rearranging gives:
M1d2=(M2−M1)x2+2M1dx
Rearranging further leads to:
(M2−M1)x2+2M1dx−M1d2=0
This is a quadratic equation in x. We can solve it using the quadratic formula:
x=−b±√b2−4ac2a
where a=M2−M1, b=2M1d, and c=−M1d2.
After solving the quadratic equation, we find:
x=d√M1√M1+√M2
The distance of the third particle from M1 is given by:
x=d√M1√M1+√M2
Topper's Solved these Questions
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - BOX-1
3 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - BOX-2
12 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 5 B (Previous Year Questions)
9 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
48 Videos
Similar Questions
Two bodies of masses 100kg and 10,000kg are at a distance of 1m apart. At what distance from 100kg on the line joining them will the resultant gravitational field intensity be zero?
View Solution.Two particles of masses "m_(1)" and m_(2)(m_(1)>m_(2))" are separated by a distance ' "d" '.The shift in the centre of mass when the two particles are interchanged.
View Solution
Knowledge Check
Two masses 'M' and '4M' are at a distance 'r' apart on the line joining them. 'P' is point where the resultant gravitational force is zero (such a point is called as null point). The distance of 'P' from the mass '4M' is
Ar5Br3C2r3D4r5Two particles of masses 'm' and '9m' are separated by a distance 'r'. At a point on the line joining them the gravitational field is zero. The gravitational potential at that point is (G = Universal constant of gravitation)
A−4GmrB−8GmrC−16GmrD−32GmrTwo particle of masses m and 2m are at a distance 3r apart at the ends of a straight line AB. C is the centre of mass of the system. The magnitude of the gravitational force on a unit mass placed at C due to the masses is
AzeroB7Gm4r2C9Gm4r2D3Gm2r2
Two particles of masses 1kg and 2kg are placed at a distance of 50cm. Find the initial acceleration of the first particle due to gravitational force.
View SolutionMass M is distributed uniformly along a line of length 2L. A particle of mass m is at a point that is at a distance a above the centre of the line on the its perpendicular bisector (Point P in figure). The gravitational force that the line exert on the particle is
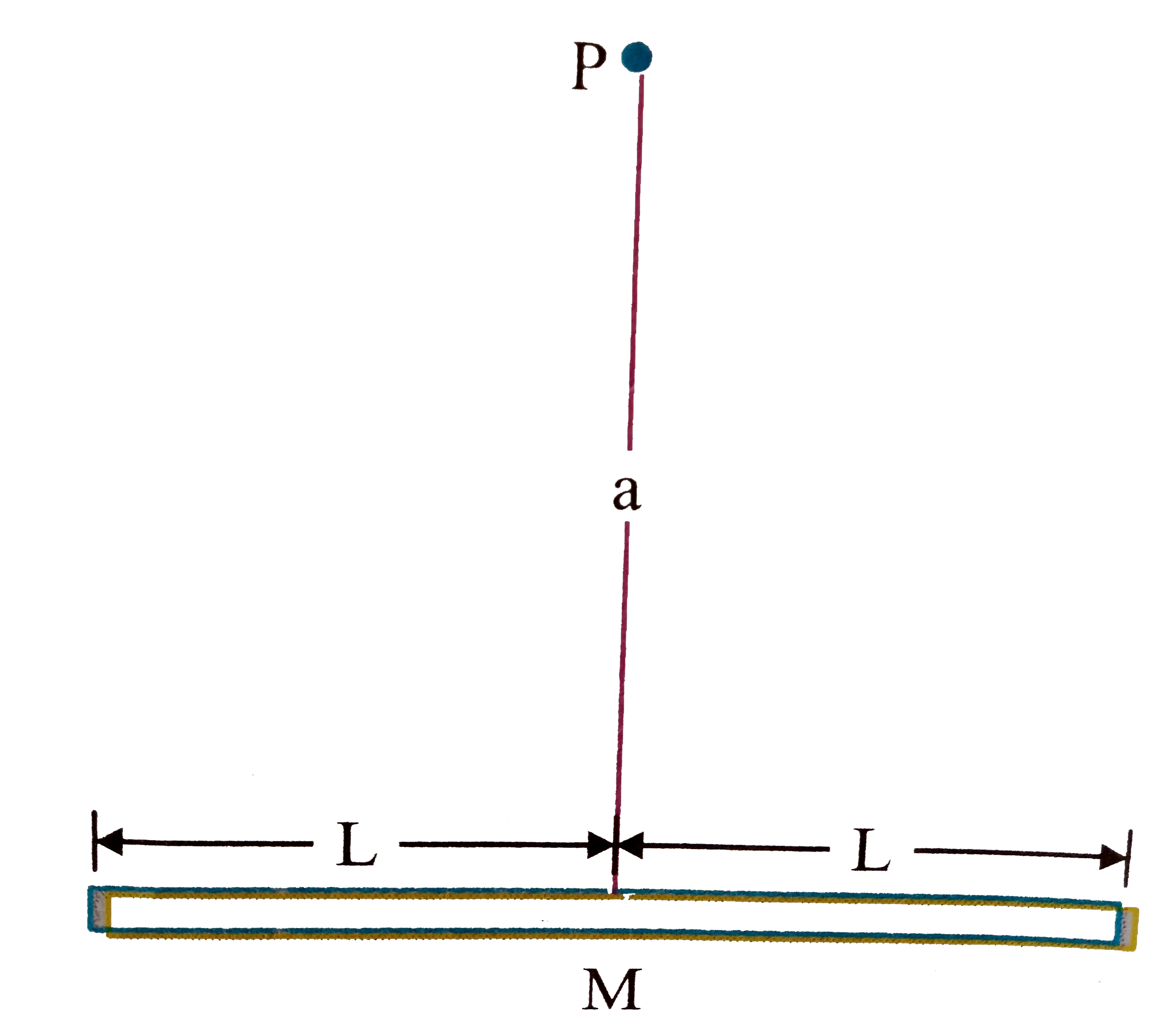
View SolutionIn the figure given below, two particles of masses m and 2m are fixed in place on an axis. Where on the axis can a third particle of mass 3m be placed (other than at infinity) so that the gravitational force on it from the first two particles is zero?

View SolutionTwo particles of mass m1 and m2, approach each other due to their mutual gravitational attraction only. Then
View SolutionTwo particles of mass m1 and m2, approach each other due to their mutual gravitational attraction only. Then
View Solution
