A block of mass 10 kg is placed on the rough horizontal surface. A pulling force F is acting on the block which makes an angle θ above the horizontal. If coefficient of friction between block and surface is 43 then minimum value of force required to just move the block is (g=10ms2)
80 N
160 N
60 N
120 N
The correct Answer is:A
To find the minimum value of the force F required to just move the block, we need to analyze the forces acting on it.
Step 1: Identify the forces acting on the block
1. Weight of the block (W): This acts downwards and is given by:
W=mg
where m=10kg and g=10m/s2.
W=10×10=100N
2. Normal force (N): This acts perpendicular to the surface. It will be affected by the vertical component of the pulling force F.
3. Frictional force (f): This opposes the motion and is given by:
f=μN
where μ=43 is the coefficient of friction.
Step 2: Resolve the pulling force F
Assuming the angle θ is above the horizontal:
- The horizontal component of the force F is:
Fx=Fcos(θ)
- The vertical component of the force F is:
Fy=Fsin(θ)
Step 3: Apply Newton's second law in the vertical direction
In the vertical direction, the forces balance out:
N+Fy=W
Substituting for Fy:
N+Fsin(θ)=mg
Thus, we can express the normal force N as:
N=mg−Fsin(θ)
Step 4: Substitute N into the frictional force equation
Now substituting N into the frictional force equation:
f=μN=μ(mg−Fsin(θ))
Substituting the values:
f=43(100−Fsin(θ))
Step 5: Set up the equation for motion
For the block to just start moving, the horizontal component of the pulling force must equal the frictional force:
Fx=f
Substituting the expressions for Fx and f:
Fcos(θ)=43(100−Fsin(θ))
Step 6: Rearranging the equation
Rearranging gives:
Fcos(θ)+43Fsin(θ)=4003
Factoring out F:
F(cos(θ)+43sin(θ))=4003
Thus, we can solve for F:
F=4003(cos(θ)+43sin(θ))
Step 7: Finding the minimum force
To find the minimum value of F, we need to analyze the function cos(θ)+43sin(θ). The minimum value occurs when θ is such that the expression is maximized. This can be done using calculus or by recognizing that the maximum occurs at specific angles.
Conclusion
The minimum value of the force F required to just move the block can be calculated using the derived formula, depending on the angle θ.
1. Weight of the block (W): This acts downwards and is given by:
W=mg
where m=10kg and g=10m/s2.
W=10×10=100N
f=μN
where μ=43 is the coefficient of friction.
Assuming the angle θ is above the horizontal:
- The horizontal component of the force F is:
Fx=Fcos(θ)
- The vertical component of the force F is:
Fy=Fsin(θ)
In the vertical direction, the forces balance out:
N+Fy=W
Substituting for Fy:
N+Fsin(θ)=mg
Thus, we can express the normal force N as:
N=mg−Fsin(θ)
Now substituting N into the frictional force equation:
f=μN=μ(mg−Fsin(θ))
Substituting the values:
f=43(100−Fsin(θ))
For the block to just start moving, the horizontal component of the pulling force must equal the frictional force:
Fx=f
Substituting the expressions for Fx and f:
Fcos(θ)=43(100−Fsin(θ))
Rearranging gives:
Fcos(θ)+43Fsin(θ)=4003
Factoring out F:
F(cos(θ)+43sin(θ))=4003
Thus, we can solve for F:
F=4003(cos(θ)+43sin(θ))
To find the minimum value of F, we need to analyze the function cos(θ)+43sin(θ). The minimum value occurs when θ is such that the expression is maximized. This can be done using calculus or by recognizing that the maximum occurs at specific angles.
The minimum value of the force F required to just move the block can be calculated using the derived formula, depending on the angle θ.
Topper's Solved these Questions
Similar Questions
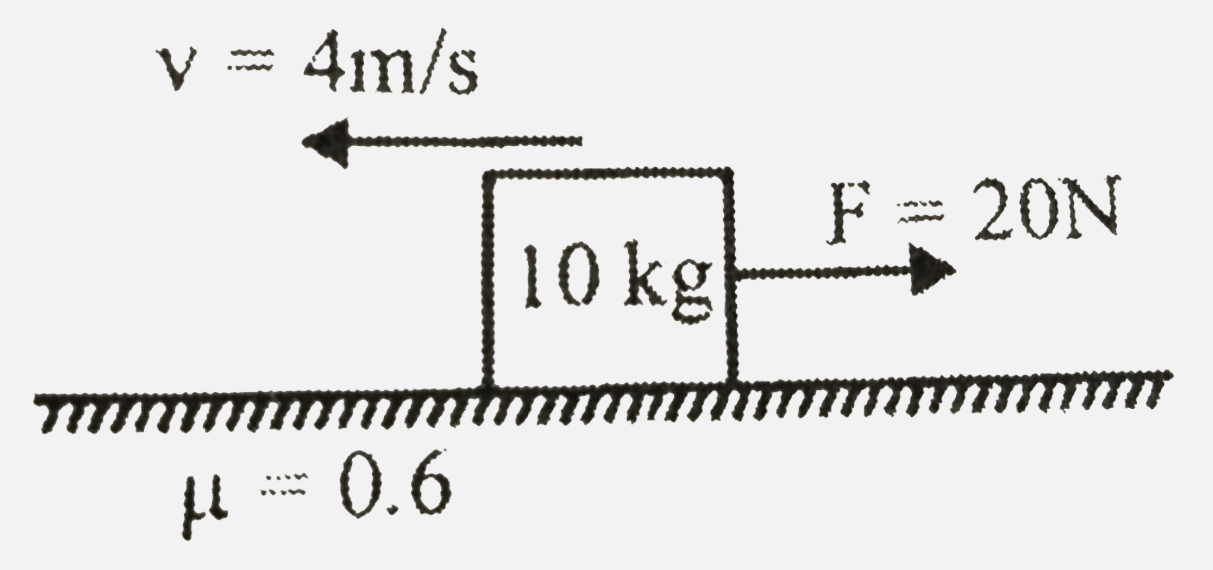
A block of mass 10 kg is moving on a rough surface as shown in figure. The frictional force acting on block is :-
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View Solution
Knowledge Check
A block of weight 200N is pulled along a rough horizontal surface at constant speed by a force of 100N acting at an angle 30∘ above the horizontal. The coefficient of kinetic friction between the block and the surface is
A0.43B0.58C0.75D0.83A block of weight 200N is pulled along a rough horizontal surface at contant speed by a force of 100N acting at an angle 30∘ above the horizontal. The coefficient of kinetic friction between the block and the surface is .
A0.43B0.58C0.75D0.83A wooden block of mass M resting on a rough horizontal surface is pulled with a force F at an angle with the horizontal. If is the coefficient of kinetic friction between the block and the surface, then acceleration of the block is -
AFM(cosϕ+μsinϕ)−μgBFsin(ϕ)MCμFcosϕD,uFsinϕ
A force F is acting at an angle θ with horizontal on a block of mass 12 kg placed on a rough 3 horizontal surface having coefficient of friction μ=34 as shown in the figure. The minimum value of force F to just move the block will be (g=10ms−2)
View SolutionA block of mass m is placed on a rough horizontal surface. If minimum force to pull the block is mg2 then coefficient of friction is :
View SolutionA block is sliding on a rough horizontal surface. If the contact force on the block is √2 times the frictional force, the coefficient of friction is
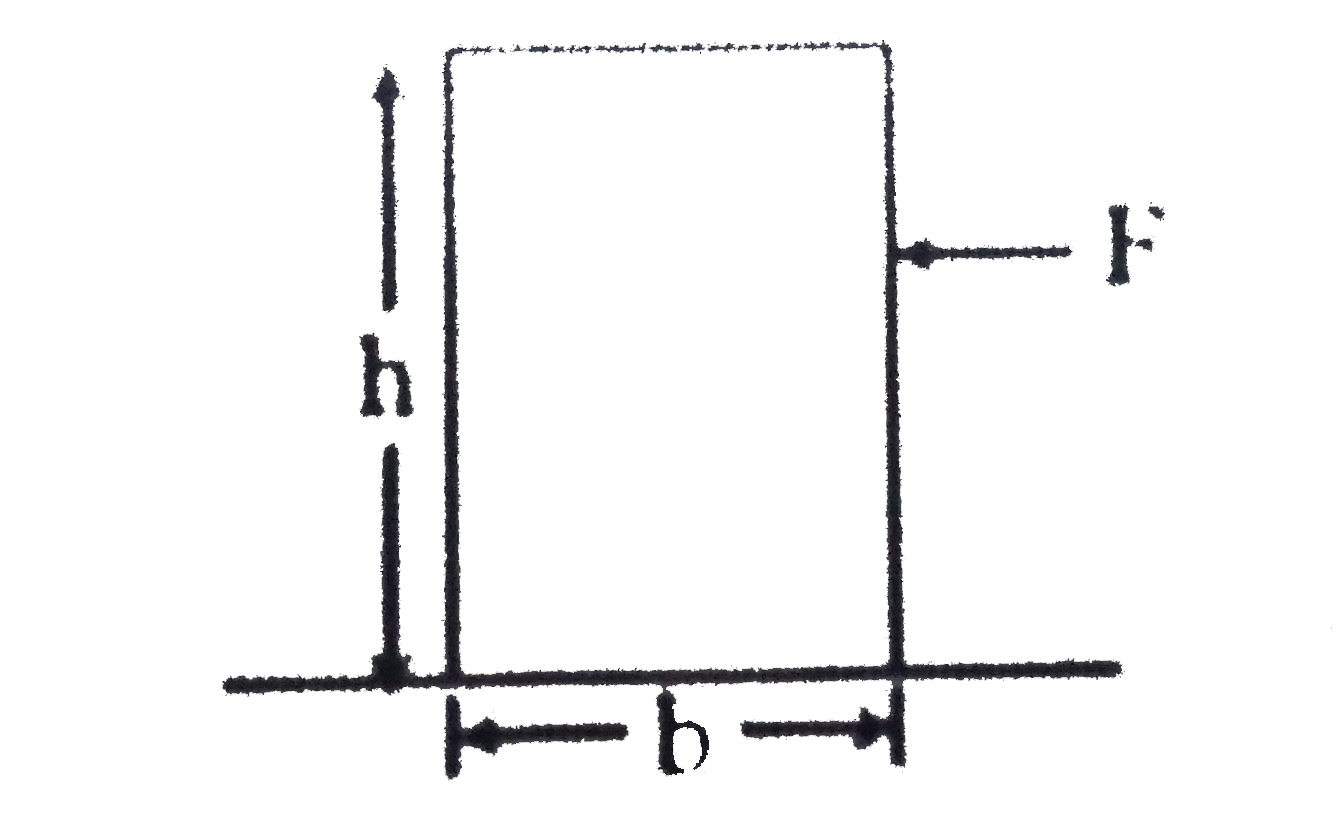
View SolutionA homogenous block of mass m, width b and height h is resting on a rough horizontal surface A horizontal force F is applied to it , which makes it to move with a constant velocity . The coefficient of friction between block and surface is μ Find the greatest height at which force F may be applied to slide the block with out tipping over
View SolutionA block of mass 3kg is placed on a rough horizontal surface (μs=0.4) . A force of 8.7N is applied on the block. The force of friction between the block and floor is .
View Solution
