A solid cylinder of denisty ρ0, cross-section area A and length l floats in a liquid ρ(>ρ0 with its axis vertical, as shown. If it is slightly displaced downward and released, the time period will be :

2π√lg
2π√ρ0lρg
2π√ρlρ0g
2π√l2g
The correct Answer is:B
Step by step video & image solution for A solid cylinder of denisty rho_(0), cross-section area A and length l floats in a liquid rho(gtrho_(0) with its axis vertical, as shown. If it is slightly displaced downward and released, the time period will be : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Fundamental)
23 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Superposition of waves interfarence, beats)
15 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Oscillations) (Energy & spring pendulum)
16 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
Consider a solid cylinder of the density ρs cross section area A and h ploating in a liquid of density ρl as shown in figure (ρl>ρs) . It is depressed sligtly and allowed to oscillation.

View SolutionAn ideal liquid having length of liquid column l is column in V-shape take as shown. If liquid is displaced, then its time period is
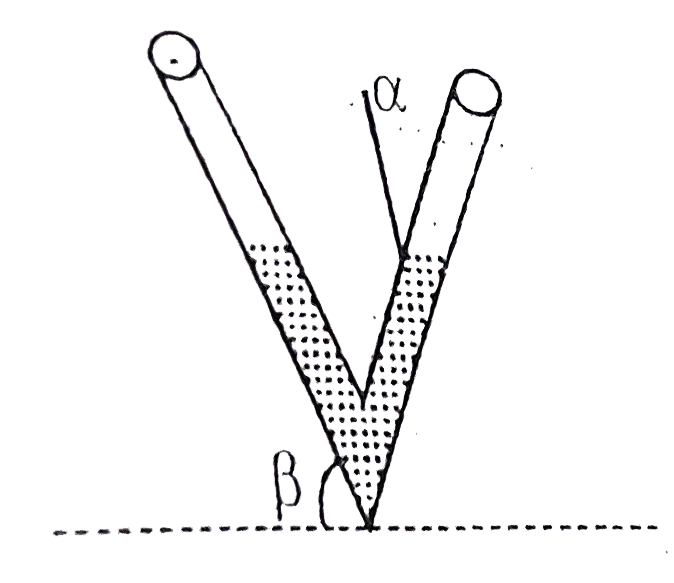
View Solution
Knowledge Check
A homogeneous solid cylinder of length L(LltH/2), cross-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid as shown in the figure. The lower density liquid is open to atmosphere having pressure P0. Then density D of solid is given by
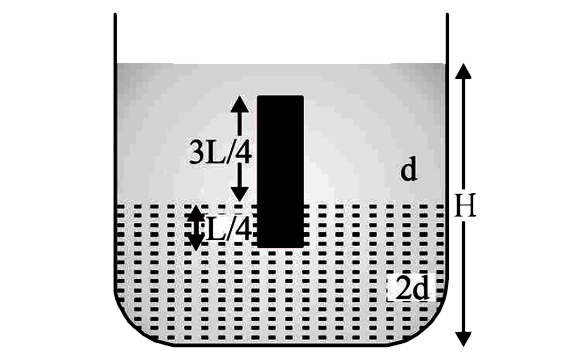 A(a) 54dB(b) 45dC(c) 4dD(d) d5
A(a) 54dB(b) 45dC(c) 4dD(d) d5A solid cylinder of length l , cross sectional area A and density 54×103kgm−3 is immersed such that it floats with its axis vertical at the liquid - liquid interface with length l/4 in the denser liquid as shown in the figure . The lesser dense liquid is open to atmospheric pressure P0. If the density of lesser dense liquid is 1.0×103 kg m−3 then the density of denser liquid will be
 A1.5×103kg m−3B2.0×103kg m−3C2.5×103kg m−3D3.0×103kg m−3
A1.5×103kg m−3B2.0×103kg m−3C2.5×103kg m−3D3.0×103kg m−3A cylinderical block of wood of mass m and area cross-section A is floating in water (density = ρ) when its axis vertical. When dressed a little and the released the block starts oscillating. The period oscillations is
A(2π√mρbgB2π√mgρAC2π√ρAgmD2π√ρAmg)
A wooden cube (density of wood ρ3 ') of side l 'floats in a liquid of density ' ρ with its upper and lower surfaces horizontal. If the cube is pushed slightly down and released, it performs simple harmonic motion of period T. Then, T is equal to 2π√xlyg. Find (x+y).
View SolutionConsider a solid cylinder of height h, density ρs, cross-sectional area A is floating in a liquid of density ρl. The frequency of vertical oscillations was found to be gahbρci,ρds when depressed slightly and released. Then what is the value of a2bcd ?
View SolutionA large tank of cross-section area A contains liquid of density ρ .A cylinder of density ρ4 ,length l=40cm ,and cross-section area a (<
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The density D of the material of the floation cylinder is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The total pressure with cylinder, at the bottom of the container is
View Solution
