If the total area goes up by 5%, and the area under wheat production goes up by 12%, then what will be the angle for wheat in the new pie-chart? (b) (c) (d)
To solve the problem step by step, we will follow the information given in the question and the video transcript.
Step 1: Understand the initial conditions
Let the total area of the pie chart be A. The area representing wheat production initially is given as a fraction of the total area.
Step 2: Calculate the initial area of wheat
The initial area of wheat production is:
Initial area of wheat=72360×A=15A
Step 3: Calculate the new total area
The total area increases by 5%, so the new total area A′ is:
A′=A+0.05A=1.05A=2120A
Step 4: Calculate the new area of wheat
The area under wheat production increases by 12%. Therefore, the new area of wheat is:
New area of wheat=15A+0.12×15A=15A×(1+0.12)=15A×1.12=112500A
Step 5: Calculate the angle for wheat in the new pie chart
To find the angle for wheat in the new pie chart, we use the formula:
Angle for wheat=(New area of wheatNew total area)×360
Substituting the values we calculated:
Angle for wheat=⎛⎝112500A2120A⎞⎠×360
Step 6: Simplify the expression
The A cancels out:
Angle for wheat=(112500×2021)×360
=(112×20500×21)×360
Step 7: Calculate the final angle
Now simplifying:
=(224010500)×360
=(2240×36010500)
Calculating this gives:
=76.8∘
Final Answer
The angle for wheat in the new pie chart is 76.8 degrees.
Let the total area of the pie chart be A. The area representing wheat production initially is given as a fraction of the total area.
The initial area of wheat production is:
Initial area of wheat=72360×A=15A
The total area increases by 5%, so the new total area A′ is:
A′=A+0.05A=1.05A=2120A
The area under wheat production increases by 12%. Therefore, the new area of wheat is:
New area of wheat=15A+0.12×15A=15A×(1+0.12)=15A×1.12=112500A
To find the angle for wheat in the new pie chart, we use the formula:
Angle for wheat=(New area of wheatNew total area)×360
Substituting the values we calculated:
Angle for wheat=⎛⎝112500A2120A⎞⎠×360
The A cancels out:
Angle for wheat=(112500×2021)×360
=(112×20500×21)×360
Now simplifying:
=(224010500)×360
=(2240×36010500)
Calculating this gives:
=76.8∘
The angle for wheat in the new pie chart is 76.8 degrees.
Topper's Solved these Questions
Similar Questions
If the total area goes up by 5%, and the area under wheat production goes up by 12%, then what will be the angle for wheat in the new pie-chart? 62.4o (b) 76.8o (c) 80.6o (d) 84.2o
View SolutionThe price of cauliflower goes up by 8% and total expenditure on cauliflowe goes up by 8% what is P.eD ?
View Solution
Knowledge Check

What product will be obtained if 'W' is treated with C6H5MgBr followed by D3O⊕ and then by heating ?A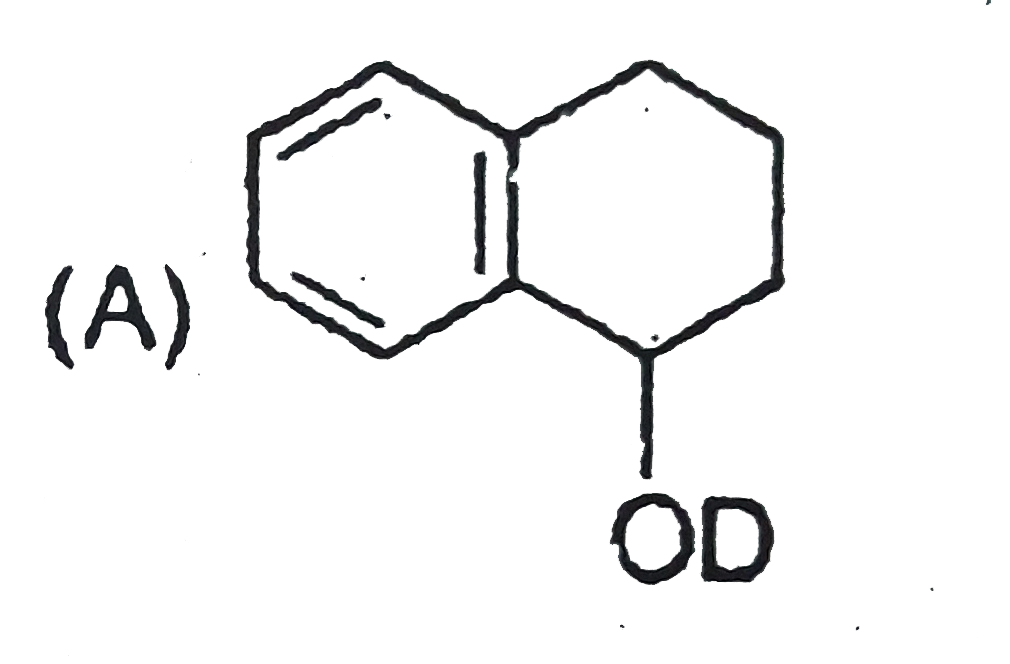 B
B C
C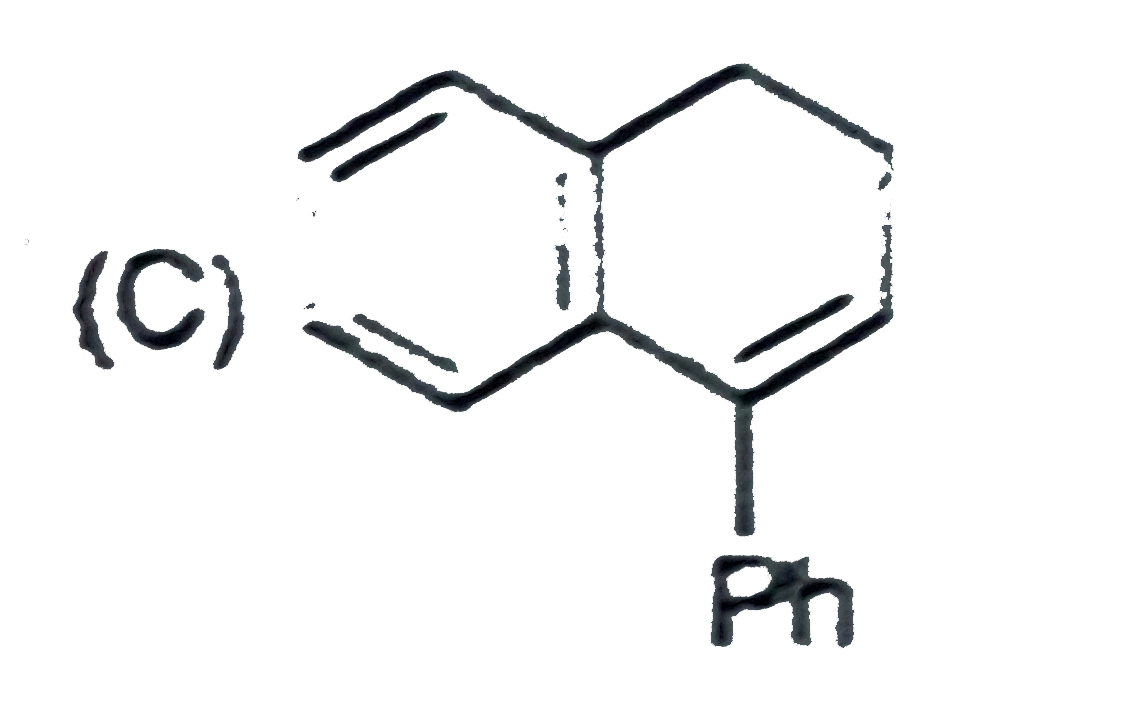 D
D
If the total area under jowar was 1.5 million acres, then what was the area (in million acres) under rice? (a) 6 (b) 7.5 (c) 9 (d) 4.5
View SolutionIf the production of wheat is 6 times that of barley, then what is the ratio between the yield per acre of wheat and barley? (a) 3 : 2 (b) 3 : 1 (c) 12 : 1 (d) 2 : 3
View SolutionWhat is the area of the triangle formed by the points O(0, 0), A(6, 0) and B(0, 4) ?
View SolutionAt what angle the hands of a clock are inclined at 15 minutes past 5? 5812o (b) 64o (c) 6712o (d) 7212o
View SolutionIf the area of a sector of a circle is 518 of the area of the circle, then the sector angle is equal to (a) 60o (b) 90o (c) 100o (d) 120o
View SolutionIf the area of a sector of a circle is 720 of the area of the circle, then the sector angle is equal to (a) 110o (b) 130o (c) 100o (d) 126o
View SolutionThrough what angle does the minute hand of a clock turn in 5 minutes? 30o (b) 32o (c) 35o (d) 36o
View Solution
