Three charges +Q, q, +Q are placed respectively, at distance, 0, d//2 and d from the origin, on the x-axis. If the net force experienced by +Q placed at x=0, is zero, then value of q is :
−Q/4
+Q/2
Q/4
−Q/2
To solve the problem, we need to find the value of charge q such that the net force acting on the charge +Q at the origin (x=0) is zero. We have three charges: +Q at x=0, q at x=d2, and +Q at x=d.
1. Identify the forces acting on the charge at the origin:
- The charge at the origin experiences forces due to the charge q at x=d2 and the charge +Q at x=d.
2. Calculate the force due to charge q:
- The distance between the charge at the origin and the charge q is d2.
- The force F1 on +Q due to q is given by Coulomb's law:
F1=kQ|q|(d2)2=k4Q|q|d2
- The direction of this force depends on the sign of q. If q is positive, F1 is repulsive (away from q), and if q is negative, F1 is attractive (towards q).
3. Calculate the force due to the second charge +Q:
- The distance between the charge at the origin and the charge +Q at x=d is d.
- The force F2 on +Q due to the charge +Q at x=d is:
F2=kQ2d2
- This force is also repulsive, acting away from the charge at x=d.
4. Set up the equation for net force to be zero:
- For the net force to be zero, the forces must balance:
F1−F2=0
- This implies:
F1=F2
- Substituting the expressions for F1 and F2:
k4Q|q|d2=kQ2d2
5. Simplify the equation:
- Cancel k and d2 from both sides:
4|q|=Q
- Therefore, we can express |q| as:
|q|=Q4
6. Determine the sign of q:
- Since the force F1 must be attractive (to balance the repulsive force F2), q must be negative:
q=−Q4
Final Answer:
The value of q is:
q=−Q4
- The charge at the origin experiences forces due to the charge q at x=d2 and the charge +Q at x=d.
- The distance between the charge at the origin and the charge q is d2.
- The force F1 on +Q due to q is given by Coulomb's law:
F1=kQ|q|(d2)2=k4Q|q|d2
- The direction of this force depends on the sign of q. If q is positive, F1 is repulsive (away from q), and if q is negative, F1 is attractive (towards q).
- The distance between the charge at the origin and the charge +Q at x=d is d.
- The force F2 on +Q due to the charge +Q at x=d is:
F2=kQ2d2
- This force is also repulsive, acting away from the charge at x=d.
- For the net force to be zero, the forces must balance:
F1−F2=0
- This implies:
F1=F2
- Substituting the expressions for F1 and F2:
k4Q|q|d2=kQ2d2
- Cancel k and d2 from both sides:
4|q|=Q
- Therefore, we can express |q| as:
|q|=Q4
- Since the force F1 must be attractive (to balance the repulsive force F2), q must be negative:
q=−Q4
The value of q is:
q=−Q4
Topper's Solved these Questions
Similar Questions
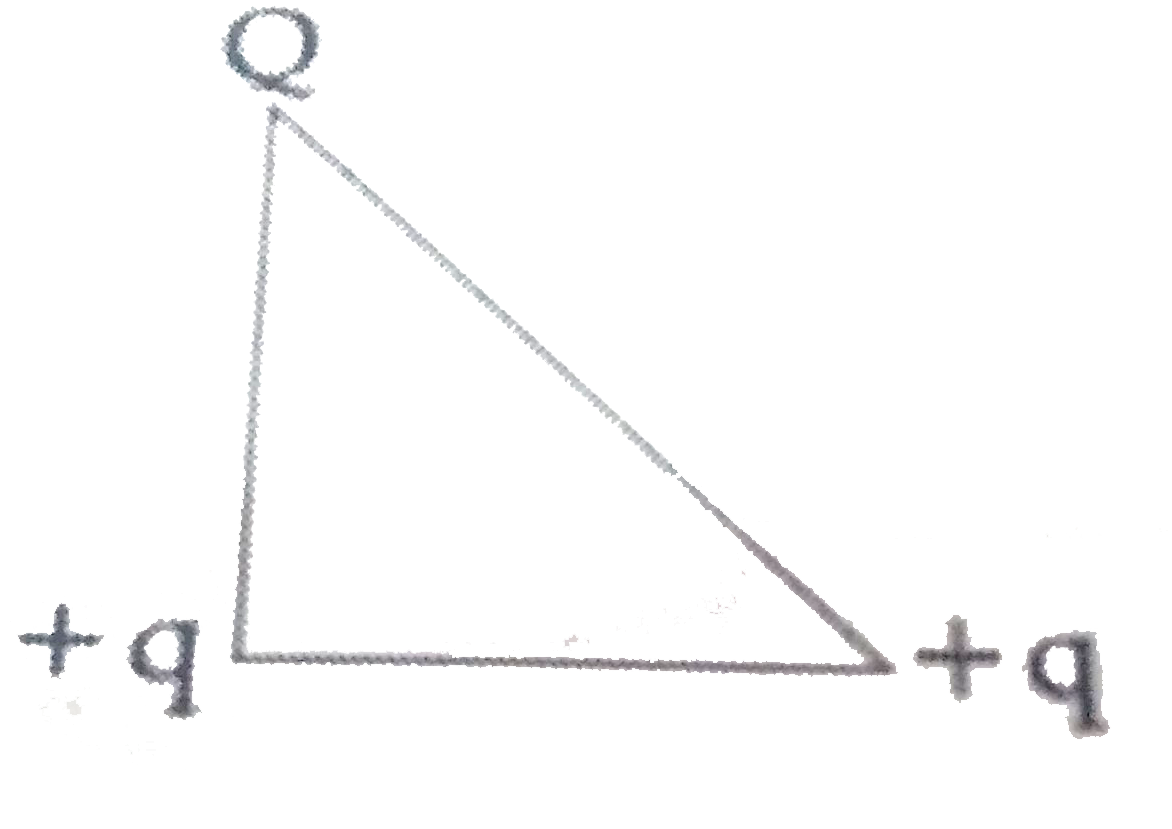
Three charges Q+q and + q are placed at the vertices of a right -angle isosceles triangle as shown below. The net eletrostatic energy of the configuration is zero if the value of Q is :
View SolutionA positive point charge q is fixed at origin. A dipole with a dipole momen →p is placed along the x-axis for away from the orgin with →p poiniting along positive x-axis .
(i) If the kinetic energy of the diople when it reachers a distance d from the origin is qp4πε0dn, then n is .
(ii) If the force experienced by the charge q at this moment is 4qpπε0d3,ˆi then x is.
View Solution
Knowledge Check
Three charges Q,(+q) and (+q) are placed at the vertices of an equilateral triangle of side l as shown in the figure. It the net electrostatic energy of the system is zero, then Q is equal to
 A(−q2)B(−q)C(+q)DZero
A(−q2)B(−q)C(+q)DZeroThree charge q,Q and −4q are placed in a straight line , line of length Lat points distant 0,L/2 and L respectively from one end. In order to make the net force on q zero, the charge Q must be equal to
A−qB−2qC−q2DqA charged spherical conductor of radius R carries a charge Q. a point charge q is placed at an outside point at a distance x from the surface of the sphere. The force experienced by the point charge will be proportional to
A1x2B(R+x)2C1(R+x)2D1(R−x)2
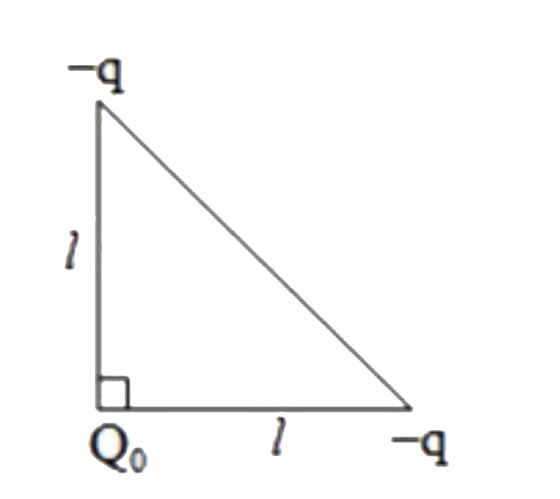
Three charges Q0 - q and q are placed at the vertices of an isosceles right angle triangle as in the future. The net electrostatic potential energy is zero if Q0 is equal to
View SolutionThree point charges Q1,Q2,Q3 in the order are placed equally spaced along a straight line. Q2 andQ3 are equal in magnitude but opposite in sign. If the net force on Q3 is zero. The value of Q1 is
View SolutionFour point charge q,−q,2Q and Q are placed in order at the corners A, B, C and D of a square. If the field at the midpoint of CD is zero then the value of q/Q is 5√5x. Find the value of x.
View SolutionA charge Q is distributed over a line of length L Another point charge q is placed at a distance r from the centre of the line distribution. Then the force experienced by q is
View SolutionA charge Q is distributed over a line of length L Another point charge q is placed at a distance r from the centre of the line distribution.Then the force experienced by q is
View Solution
