Two masses m and m2 are connected at the two ends of a massless rigid rod of length l. The rod is suspended by a thin wire of torsional constant k at the centre of mass of the rod-mass system(see figure). Because of torsional constant k, the restoring torque is τ=kθ for angular displacement θ. If the rod is rotated by θ0 and released, the tension in it when it passes through its mean position will be :
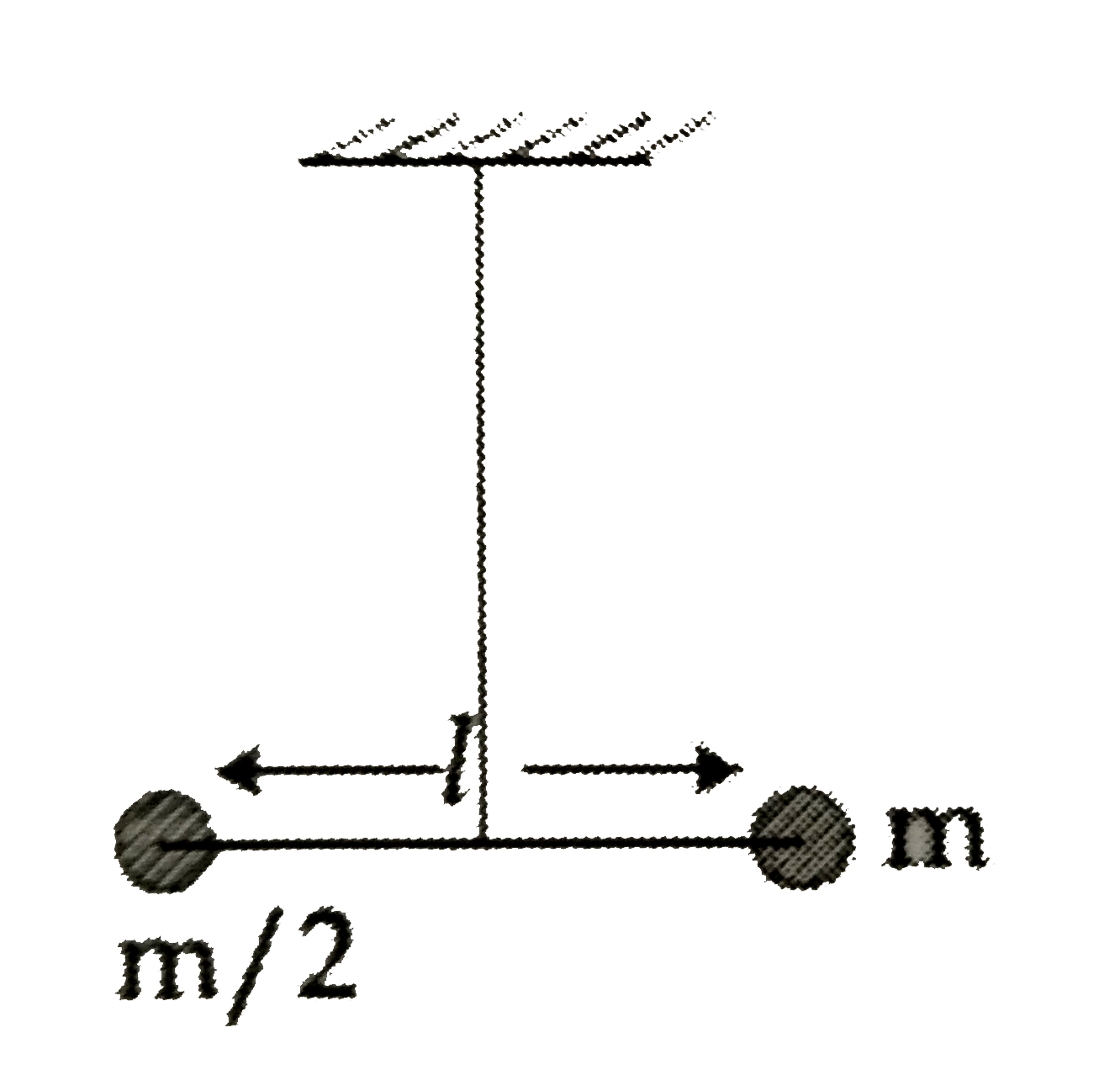
3kθ20l
2kθ20l
kθ20l
kθ202l
Step by step video & image solution for Two masses m and (m)/(2) are connected at the two ends of a massless rigid rod of length l. The rod is suspended by a thin wire of torsional constant k at the centre of mass of the rod-mass system(see figure). Because of torsional constant k, the restoring torque is tau=ktheta for angular displacement theta. If the rod is rotated by theta_(0) and released, the tension in it when it passes through its mean position will be : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
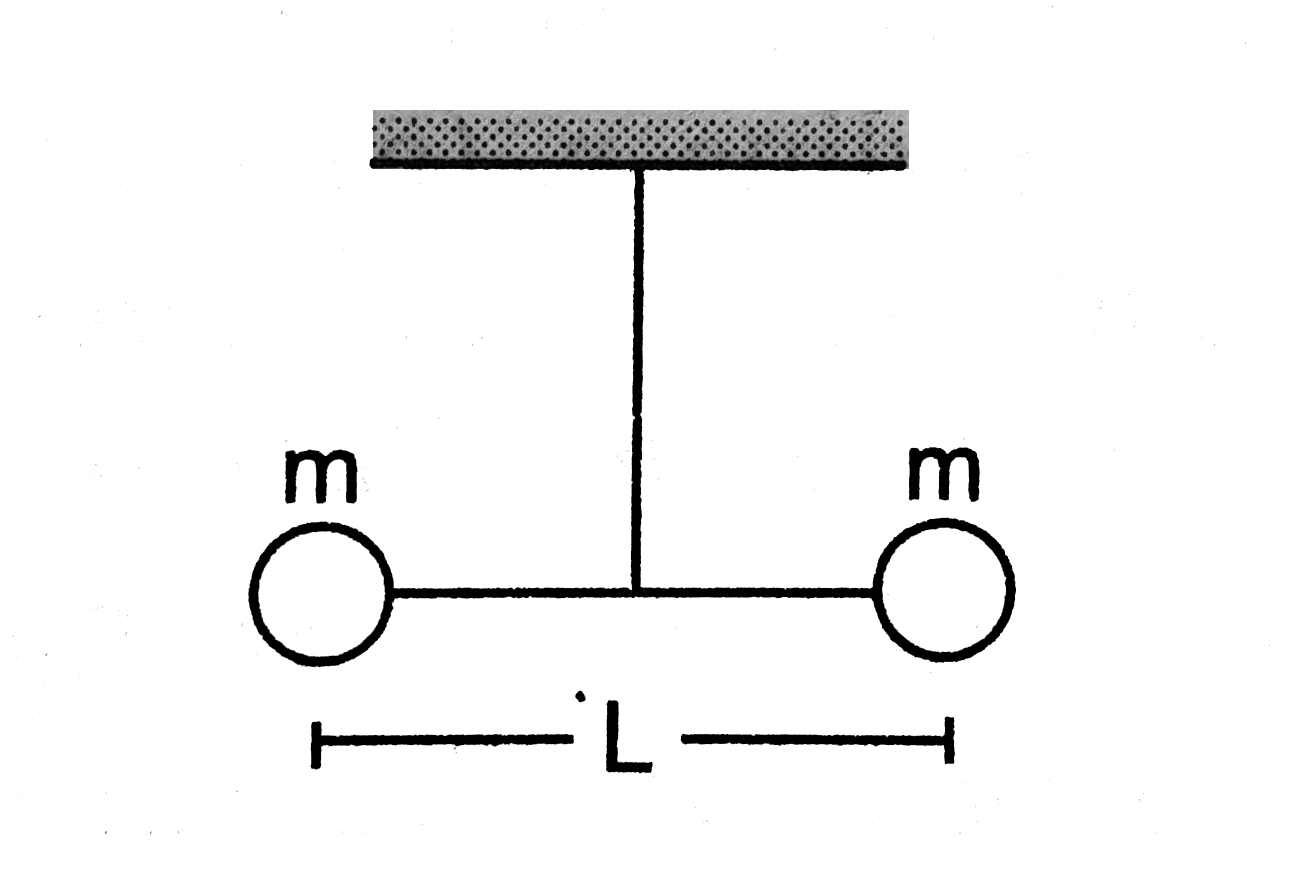
Two small balls, each of mass m are connected by a light rigid rod of length L. The system is suspended from its centre by a thin wire of torsional constant k. The rod is rotated about the wire through an angle θ0 and released. Find the tension in the rod as the system passes through the mean position.
View SolutionTwo point masses m and 4m are connected by a light rigid rod of length l at the opposite ends. Moment of inertia of the system about an axis perpendicular to the length and passing through the centre of mass is
View Solution
Knowledge Check
Two masses each of mass M are attached to the end of a rigid massless rod of length L. The moment of interia of the system about an axis passing centre of mass and perpendicular to its length is.
AML24BML22CML2D2ML2Two balls of masses m and 2m are attached to the ends of a light rod of length L. The rod rotates with an angular speed ω about an axis passing through the center of mass of system and perpendicular to the plane. Find the angular momentum of the system about the axis of rotation.
A23mωL2B13ω2LmC23ω2LmD13LmTwo particles, each of mass m and charge q are attached to the two ends of a light rigid rod of length 2R. The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
AqmB2qmCq2mDqπm
A uniform rod of mass m and length l is pivoted smoothly at O. A horizontal force acts at the bottom of the rod.
a. Find the angular velocity of the rod as the function of angle of rotation θ.
b.What is the maximum angular displacement of the rod?
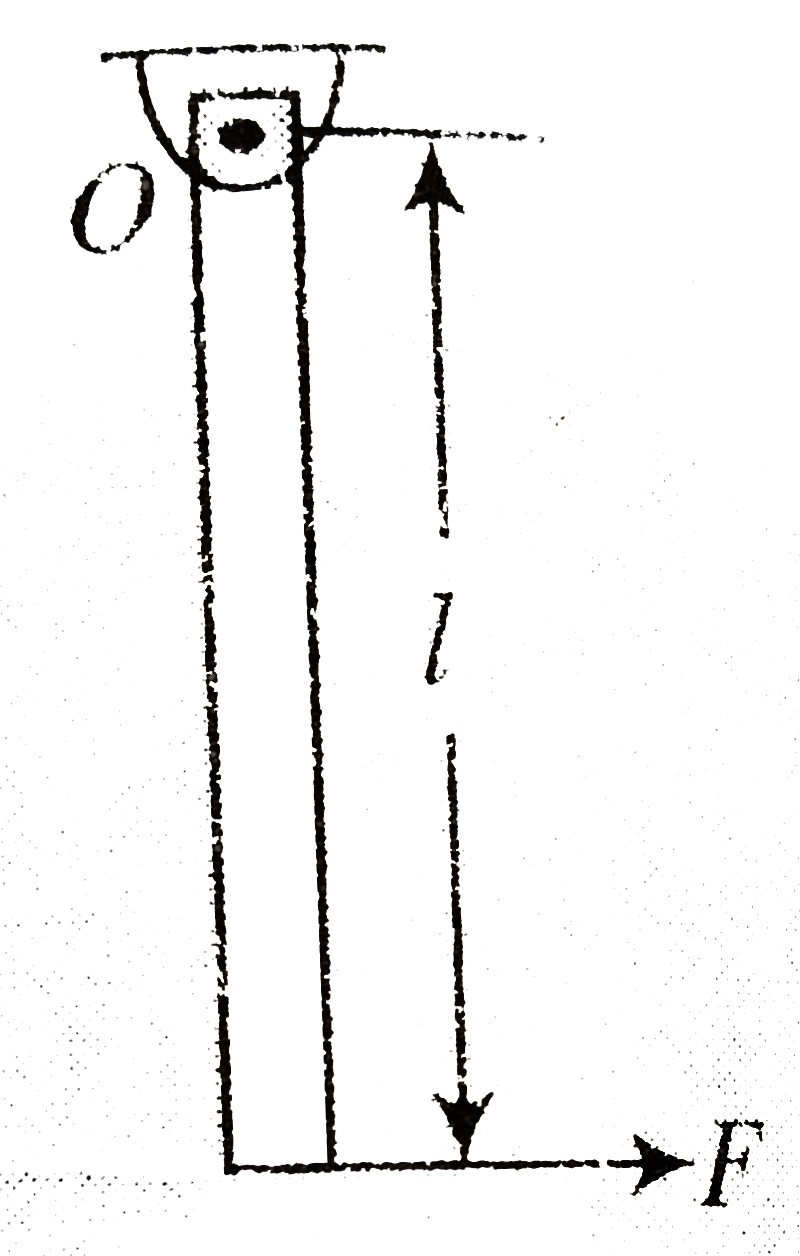
View SolutionA rigid rod of mass m & length l is pivoted at one of its ends. If it is released from its horizontal position, find the speed of the centre of mass of the rod when it becomes vertical.
View SolutionTwo balls of masses m and 2m are attached to the ends of a light rod of length L. The rod rotates with an angular speed ω about an axis passing through the center of mass of system and perpendicular to the plane. Find the angular momentum of the system about the axis of rotation.
View SolutionTwo particles , each of mass m and charge q, are attached to the two ends of a light rigid rod of length 2R . The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
View SolutionTwo particles of masses m1 and m2 are connected with a rigid rod of length l. If a force F acts perpendicular to the rod then (a1&a2 are instantaneous of m1&m2)

View Solution
