A simple pendulum , made of a string of length l and a bob of mass m, is released from a small angle θ0 it strikes a block of mass M, kept on a horizontal surface at its lowest point of oscil,ations , elastically , it bounces back and goes up to an angle θ)(1−) then M is given by :
m2(θ0+θ1θ0−θ1)
m(θ0−θ1θ0+θ1)
m(θ0+θ1θ0−θ1)
m2(θ0−θ1θ0+θ1)
To solve the problem, we will follow these steps:
Step 1: Determine the potential energy of the pendulum bob at the initial angle θ₀.
The height h of the bob when it is at angle θ₀ can be calculated as:
h=L−Lcosθ₀=L(1−cosθ₀)
The potential energy (PE) at this height is given by:
PE=mgh=mgL(1−cosθ₀)
Step 2: Calculate the kinetic energy of the bob at the lowest point of the swing.
At the lowest point, all potential energy is converted into kinetic energy (KE):
KE=12mv2
Setting the potential energy equal to the kinetic energy gives us:
mgL(1−cosθ₀)=12mv2
Cancelling m from both sides, we find:
v2=2gL(1−cosθ₀)
Thus, the speed v of the bob just before the collision is:
v=√2gL(1−cosθ₀)
Step 3: Apply conservation of momentum during the elastic collision.
Before the collision, the momentum of the system is:
pinitial=mv
After the collision, let v′ be the speed of the bob after the collision and V be the speed of the block of mass M. The momentum after the collision is:
pfinal=mv′+MV
By conservation of momentum:
mv=mv′+MV(1)
Step 4: Apply conservation of kinetic energy during the elastic collision.
For elastic collisions, kinetic energy is also conserved:
12mv2=12mv′2+12MV2
This simplifies to:
mv2=mv′2+MV2(2)
Step 5: Express v′ in terms of V.
From equation (1), we can express v′:
v′=mv−MVm
Step 6: Substitute v into the kinetic energy equation.
Substituting v=√2gL(1−cosθ₀) into equation (2):
m(2gL(1−cosθ₀))=m(mv−MVm)2+MV2
Step 7: Solve for M.
After substituting and simplifying, we can isolate M in terms of θ₀ and θ₁. The final expression will yield:
M=m(1−cosθ₀)(1−cosθ₁)
Final Result
The mass M in terms of m, θ₀, and θ₁ is:
M=m(1−cosθ₀)(1−cosθ₁)
h=L−Lcosθ₀=L(1−cosθ₀)
PE=mgh=mgL(1−cosθ₀)
KE=12mv2
Setting the potential energy equal to the kinetic energy gives us:
mgL(1−cosθ₀)=12mv2
Cancelling m from both sides, we find:
v2=2gL(1−cosθ₀)
Thus, the speed v of the bob just before the collision is:
v=√2gL(1−cosθ₀)
pinitial=mv
After the collision, let v′ be the speed of the bob after the collision and V be the speed of the block of mass M. The momentum after the collision is:
pfinal=mv′+MV
By conservation of momentum:
mv=mv′+MV(1)
12mv2=12mv′2+12MV2
This simplifies to:
mv2=mv′2+MV2(2)
v′=mv−MVm
m(2gL(1−cosθ₀))=m(mv−MVm)2+MV2
M=m(1−cosθ₀)(1−cosθ₁)
M=m(1−cosθ₀)(1−cosθ₁)
Topper's Solved these Questions
Similar Questions
A simple pendulum of length l and consisting of a ball of mass m is released from a position making an angle θ=cos−1 (0.8) with the vertical and strikes at its lowest position a block of mass M resting on a rough horizontal plane. If the coefficient of kinetic friction between the plane and the block is 0.2 find
(a) How long the block will move along the plane, if the ball of the pendulum rebounds to an angle β=cos−1 (0.9)A
(b) The coefficient of restitution, use Mm=10 and 1= 1 m
View SolutionA simple pendulm has a length L and a bob of mass M. The bob is vibrating with amplitude a .What is the maximum tension in the string?
View Solution
Knowledge Check
The bob of a simple pendulum (mass m and length l ) dropped from a horizontal position strikes a block of the same mass elastically placed on a horizontal frictionless table. The K.E. of the block will be
A2 mglBmg//2CmglD0The bob of a simple pendulum (mass m and length l ) dropped from a horizontal position strikes a block of the same mass elastically placed on a horizontal frictionless table. The K.E. of the block will be
A2 mglBmgl 2CmglD0A simple pendulum of length l and mass (bob) m is suspended vertically. The string makes an angle θ with the vertical. The restoring force acting on the pendulum is
AmgtanθB−mgsinθCmgsinθD−mgcosθ
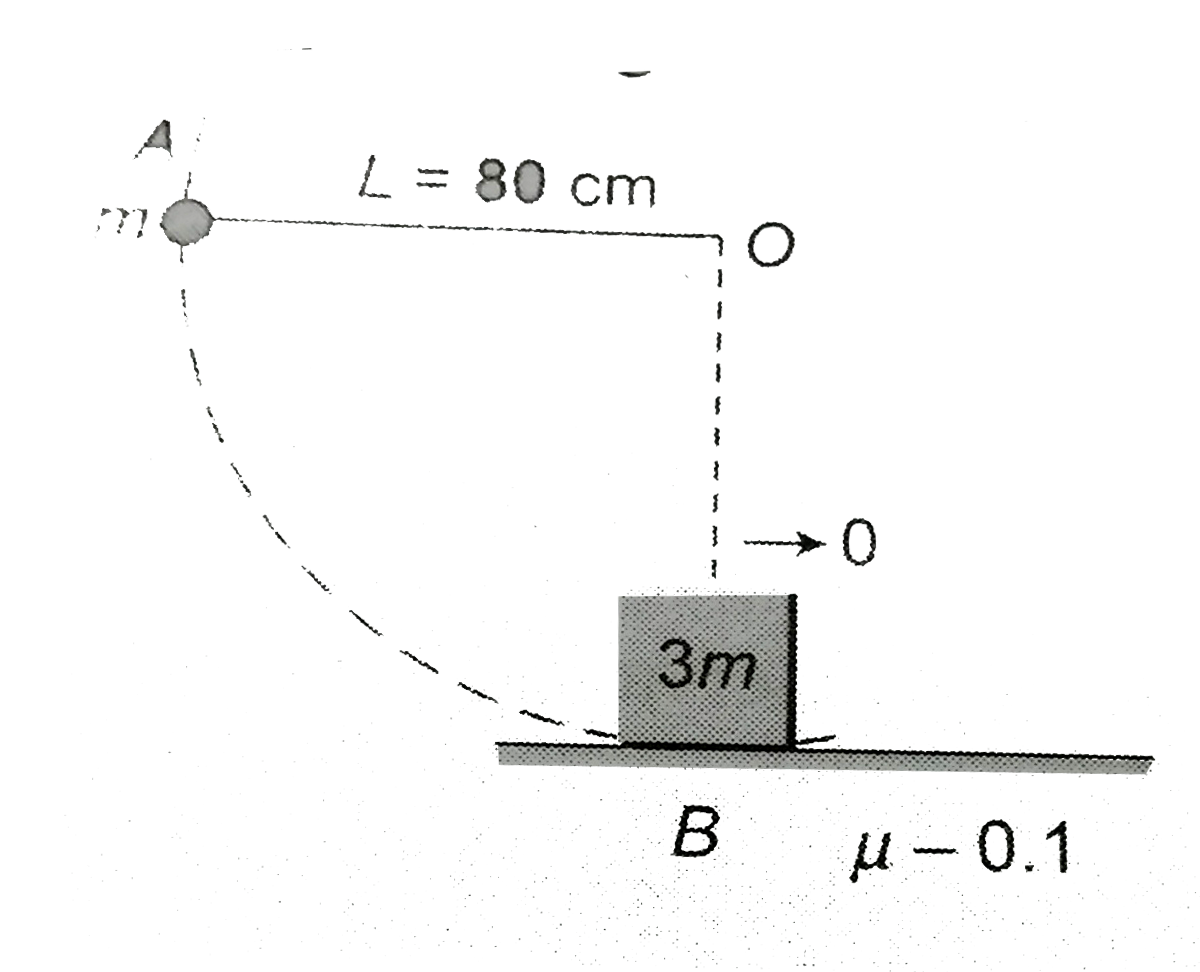
The ball A of mass m is released when the string is horizontal. It strikes a block B of mass 3m kept on a rough surface of friction coefficient μ=0.1. If a head on elastic collision takes place , find the maximum distance travelled by the block on a rough surface.
View SolutionA simple pendulum of length l and with a bob of mass m moving alon a circular are of angle θ in a vertical plane. A sphere of mass m is placed at the end of the circular arc. What momentum will be given to the sphere by the moving bob?
View SolutionIf a simple pendulum of mass m is released from a horizontal position, find the tension in the string as a function of the angle θ with the horizontal.
View SolutionA simple pendulum has a string of length l and bob of mass m. When the bob is at its lowest position , it is given the minimum horizontal speed necessary for it to move in a circular path about the point point of suspension. The tension in the string at the lowest position if the bob is
View SolutionA simple pendulum of mass m and length L is held in horizontal position. If it is released from this position, then find the angular momentum of the bob about the point of suspension when it is vertically below the point of suspension.
View Solution
