OA, OB, OC are the sides of a rectangular parallelopiped whose diagonals are OO', AA' , BB' and CC' . D is the centre of the rectangle AC'O'B' and D' is the centre of the rectangle O'A'CB' . If the sides OA, OB , OC are in the ratio 1:2:3 , the angle∠DOD' is equal to
A
cos−1(24)√697
B
cos−1(22)√619
C
sin−1(24)√697
D
sin−1(22)√619
Text Solution
The correct Answer is:A
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
If OA=a, OB=b, OC=c are the co-terminus edges of regular parallelopiped, then the shortest distance between the diagonal and the side OB not meeting the diagonal is
Abc√b2+c2Bca√c2+a2Cab√a2+b2Dabc√a2+b2+c2If OA=a, OB=b, OC=c are the co-terminus edges of regular parallelopiped, then the shortest distance between the diagonal and the side OA not meeting the diagonal is
Abc√b2+c2Bca√c2+a2Cab√a2+b2Dabc√a2+b2+c2Let ABCD be a parallelogram whose diagonals intersect at P and O be the origin, then OA+OB+OC+OD equals
AOPB2OPC3OPD4OP
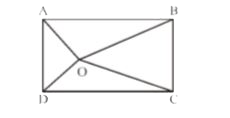
O is a point situated inside a rectangle ABCD. If sides OA, OC and OD are 6 cm, 8 cm and 6 cm respectively, then find the value of OB-
View SolutionIn the figure shown, OABC is a rectangle with OA=3 units, OC = 4 units. If BD = 2.5 units, then the slope of the diagonal OB is equal to
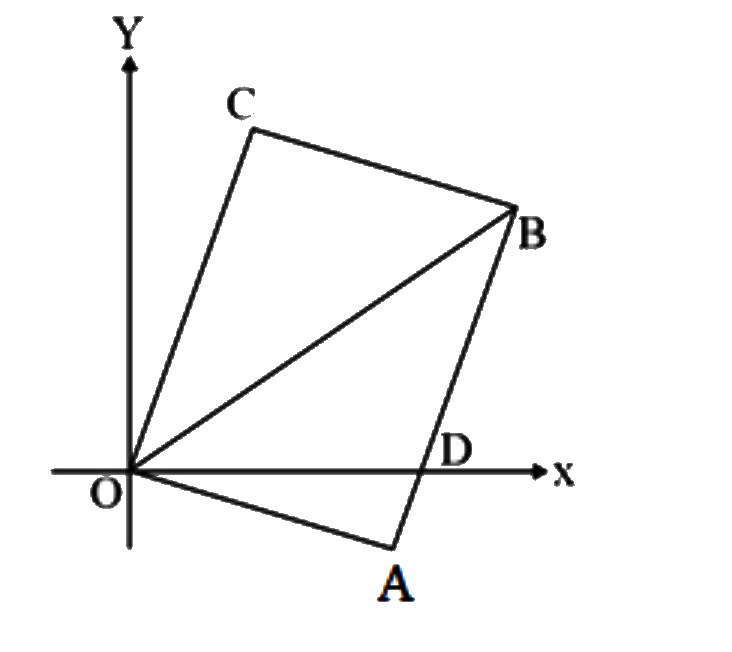
View SolutionIn the figure shown, OABC is a rectangle with OA=3 units, OC = 4 units. If BD = 2.5 units, then the slope of the diagonal OB is equal to

View SolutionA point O in the interior of a rectangle ABCD is joined with each of the vertices A, B, C and D . Prove that OB2+OD2=OC2+OA2
View SolutionPerpendicular bisectors of the sides AB and AC of a triangle ABC meet at O.
What is the relation between the distances OA, OB and OC ?
View Solution
