A 6090 kg space probe moving nose-first toward Jupiter at 120 m/s relative to the Sun fires its rocket engine, ejecting 70.0 kg of exhaust at a speed of 253 m/s relative to the space probe. What is the final velocity of the probe?
The correct Answer is:123 m/s
To solve the problem of finding the final velocity of the space probe after it ejects exhaust, we will use the principle of conservation of momentum. Here’s a step-by-step breakdown of the solution:
Step 1: Identify the Given Information
- Mass of the space probe (m₁) = 6090 kg
- Initial velocity of the space probe (u₁) = 120 m/s (toward Jupiter)
- Mass of the exhaust (m₂) = 70 kg
- Speed of the exhaust relative to the space probe (v₂') = 253 m/s (in the opposite direction)
Step 2: Calculate the Speed of the Exhaust Relative to the Sun
The speed of the exhaust relative to the Sun (v₂) can be calculated by adding the speed of the exhaust relative to the probe to the speed of the probe itself. Since the exhaust is ejected in the opposite direction to the probe's motion, we will subtract the speed of the probe from the speed of the exhaust.
v₂=u₁−v₂′=120m/s−253m/s=−133m/s
Step 3: Apply Conservation of Momentum
The total momentum before the exhaust is ejected must equal the total momentum after the exhaust is ejected.
Initial Momentum (P_initial):
Pinitial=m₁⋅u₁=6090kg⋅120m/s=730800kg m/s
Final Momentum (P_final):
After the exhaust is ejected, the mass of the probe becomes (m₁ - m₂) and its final velocity is v. The momentum of the exhaust can be calculated as m₂ times its velocity v₂.
Pfinal=(m₁−m₂)⋅v+m₂⋅v₂
Pfinal=(6090kg−70kg)⋅v+70kg⋅(−133m/s)
Step 4: Set Initial Momentum Equal to Final Momentum
Setting the initial momentum equal to the final momentum gives us:
730800kg m/s=(6020kg)⋅v+70kg⋅(−133m/s)
Calculating the momentum of the exhaust:
70⋅(−133)=−9310kg m/s
Now substituting back into the equation:
730800=6020⋅v−9310
Step 5: Solve for Final Velocity (v)
Rearranging the equation to solve for v:
6020⋅v=730800+9310
6020⋅v=739110
v=7391106020≈122.8m/s
Step 6: Conclusion
The final velocity of the space probe after ejecting the exhaust is approximately 122.8 m/s toward Jupiter.
---
- Mass of the space probe (m₁) = 6090 kg
- Initial velocity of the space probe (u₁) = 120 m/s (toward Jupiter)
- Mass of the exhaust (m₂) = 70 kg
- Speed of the exhaust relative to the space probe (v₂') = 253 m/s (in the opposite direction)
The speed of the exhaust relative to the Sun (v₂) can be calculated by adding the speed of the exhaust relative to the probe to the speed of the probe itself. Since the exhaust is ejected in the opposite direction to the probe's motion, we will subtract the speed of the probe from the speed of the exhaust.
The total momentum before the exhaust is ejected must equal the total momentum after the exhaust is ejected.
Pinitial=m₁⋅u₁=6090kg⋅120m/s=730800kg m/s
After the exhaust is ejected, the mass of the probe becomes (m₁ - m₂) and its final velocity is v. The momentum of the exhaust can be calculated as m₂ times its velocity v₂.
Pfinal=(6090kg−70kg)⋅v+70kg⋅(−133m/s)
Setting the initial momentum equal to the final momentum gives us:
Rearranging the equation to solve for v:
6020⋅v=739110
v=7391106020≈122.8m/s
The final velocity of the space probe after ejecting the exhaust is approximately 122.8 m/s toward Jupiter.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Single Correct Choice )47videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (More than One Correct Choice)5videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Integer )4videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTION (INTEGER TYPE)3videos
CAPACITANCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Practice Questions (Integer Type)3videos
CIRCUITS
Similar Questions
A plice siren emits a sound wave of frequency 440 Hz. The speed of sound is 332 m/s. if the siren is moving away from the listerner with a speed of 18 m/s relative to the air and the listerner is moving towards the siren with a speed of 68 m/s relative to the air, then what frequency does the listern hear?
View SolutionA police siren emits a sound wave of frequency 440 Hz. The speed of sound is 332 m/s. if the siren is moving away from the listerner with a speed of 18 m/s relative to the air and the listerner is moving towards the siren with a speed of 68 m/s relative to the air, then what frequency does the listern hear?
View Solution
Knowledge Check
- Question 1 - Select One
A 3.0-kg cart moving to the right with a speed of 1.0 m/s has a head-on collision with a 5.0-kg cart that is initially moving to the left with a speed of 2.0 m/s. After the collision, the 3.0-kg cart is moving to the left with a speed of 1.0 m/s. What is the final velocity of the 5.0-kg cart?
Azero m/sB0.80 m/s to the rightC0.80 m/s to the leftD2.0 m/s to the right - Question 2 - Select One
Two boats are heading away from shore. Boat 1 heads due north at a speed of 3.00 m/s relative to the shore. Relative to Boat 1, Boat 2 is moving 30.0∘ north of east at a speed of 1.60 m/s. A passenger on Boat 2 walks due east across the deck at a speed of 1.20 m/s relative to Boat 2. What is the speed of the passenger relative to the shore?
A4.60 m/sB2.71 m/sC2.53 m/sD3.14 m/s - Question 3 - Select One
A rocket of mass 120kg. Is fired in the gravity free space is ejected gases with velocity 600 m/s at the rate of 1kg/s. what will be the initial accleration of the rocket:-
A1m/s2B5m/s2C10m/s2D15m/s2
A space shuttle of mass M, moving at 4000 kph relative to earth ejects a capsule backward of mass M/5. if speed of ejection of capsule is 120 kph relative to state of shuttle before ejection, find the final velocity of the shuttle.
View SolutionA rocket with an initial mass of 1000kg, is launched vertically upward from rest under gravity. The rocket burns fuel at the rate of 10kg per second. The burnt matter is ejected vertically downwards with a speed of 2000m/s relative to the rocket . Find the velocity of the rocket after 1min of start.
View SolutionA boat is traveling relative to the water at a speed of 5.0 m/s due south. Relative to the boat, a passenger walks toward the back of the boat at a speed of 1.5 m/s. What is the magnitude and direction of the passenger's velocity relative to the water?
View SolutionAn aircraft carrier has a speed of 13.0 m/s relative to the water. A jet is catapulted from the deck and has a speed of 67.0 m/s relative to the water. The engines produce a 1550-Hz whine, and the speed of sound is 343 m/s. What is the frequency of the sound heard by the crew on the ship?
View SolutionA three part rocket begins intact as a single object in distant outer space, travlling to the right at 4.0km/h. The first stage (m1=950,000kg) explodes away from the rear of the rocket, with an unknown final velocity (vtf). Later, the second stage (m2=550,000kg) explodes away from teh rear with a final velocity to the right at 6.0km/s. The third stage (m2=350,000kg) ends up with a final velocity to the right of 13.0km/s. (All three move only along the x−axis . Ignore gravity. Assume that all parts of the rocket have constant masses.)
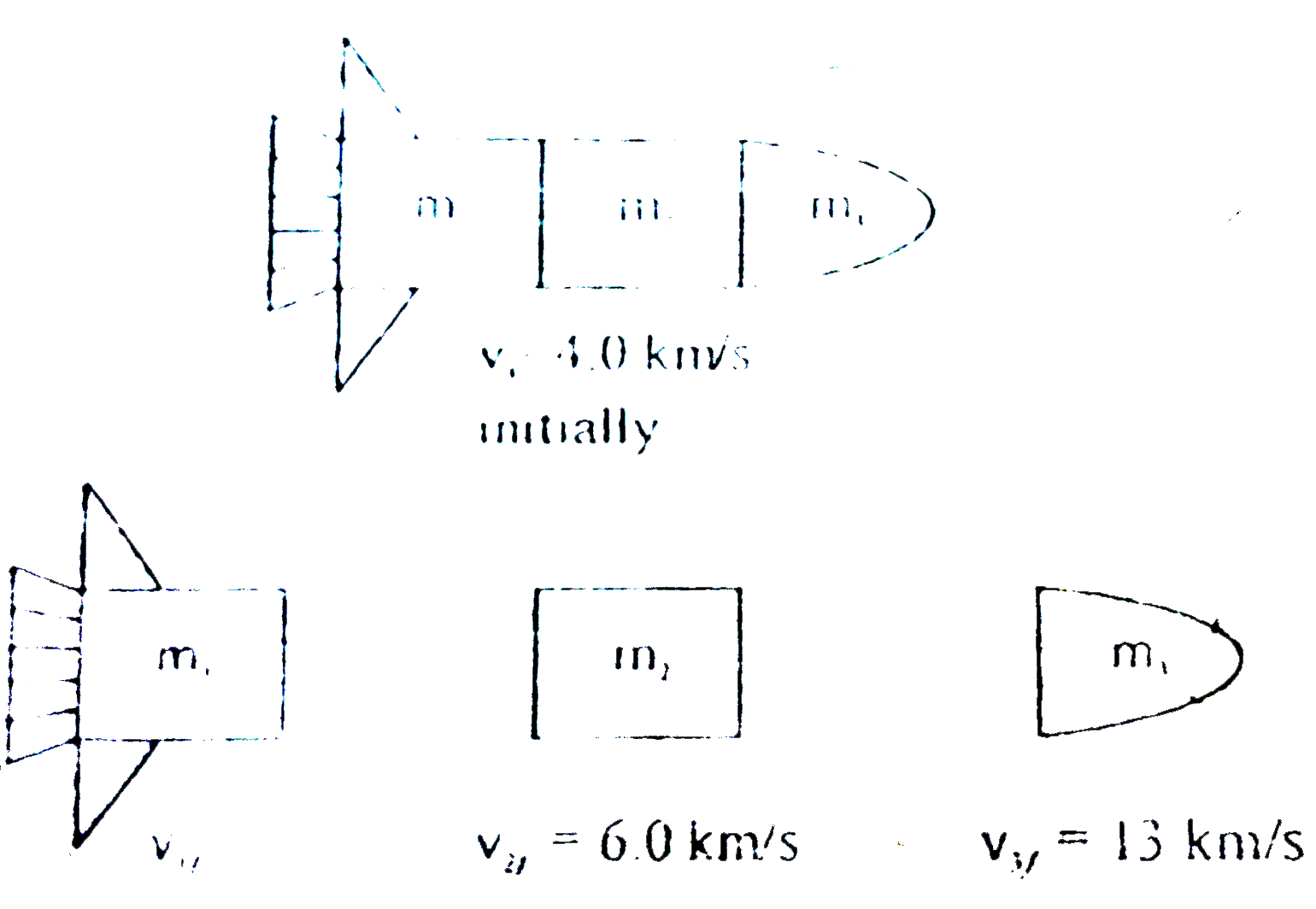
What is the final velocity (v1f) of the first stage.View Solution

