A (hypothetical) large slingshot is stretched 2.30 m to launched a 170 g projectile with speed sufficient to escape from Earth (11.2km/s). Assume the elastic bands of the slingshot obey Hooke's law.
Assume that an average person can be exert a force of 490 N. How many people are required to stretch the elastic bands?
9.5×103
1.89×104
3.78×104
2.85×104
The correct Answer is:B
To solve the problem of how many people are required to stretch the elastic bands of a slingshot, we will follow these steps:
Step 1: Understand the problem
We have a slingshot that stretches 2.30 m to launch a projectile of mass 170 g (0.17 kg) at a speed of 11.2 km/s (which is the escape velocity). We need to find out how many people are needed to exert the force required to stretch the elastic bands.
Step 2: Convert units
Convert the mass of the projectile from grams to kilograms and the speed from km/s to m/s.
- Mass of the projectile, m=170g=0.17kg
- Speed of the projectile, v=11.2km/s=11.2×103m/s
Step 3: Use energy conservation
The elastic potential energy stored in the slingshot when stretched is equal to the kinetic energy of the projectile when launched.
The elastic potential energy (EPE) is given by:
EPE=12kx2
where k is the spring constant and x is the stretch (2.30 m).
The kinetic energy (KE) of the projectile is given by:
KE=12mv2
Step 4: Set the energies equal
Setting the elastic potential energy equal to the kinetic energy:
12kx2=12mv2
We can cancel the 12 on both sides:
kx2=mv2
Step 5: Solve for the spring constant k
Rearranging the equation gives:
k=mv2x2
Substituting the values:
k=0.17kg×(11.2×103m/s)2(2.30m)2
Calculating v2:
v2=(11.2×103)2=1.2544×108m2/s2
Calculating x2:
x2=(2.30)2=5.29m2
Now substituting these values into the equation for k:
k=0.17×1.2544×1085.29≈4.0×106N/m
Step 6: Calculate the force required to stretch the slingshot
Using Hooke's law, the force F required to stretch the slingshot is given by:
F=kx
Substituting the values:
F=4.0×106N/m×2.30m=9.2×106N
Step 7: Determine the number of people required
If one person can exert a force of 490 N, the number of people N required is:
N=FForce per person=9.2×106N490N≈18878.57
Rounding up, we find that approximately 18879 people are required to stretch the elastic bands.
Final Answer
Approximately 18879 people are required to stretch the elastic bands of the slingshot.
---
We have a slingshot that stretches 2.30 m to launch a projectile of mass 170 g (0.17 kg) at a speed of 11.2 km/s (which is the escape velocity). We need to find out how many people are needed to exert the force required to stretch the elastic bands.
Convert the mass of the projectile from grams to kilograms and the speed from km/s to m/s.
- Mass of the projectile, m=170g=0.17kg
- Speed of the projectile, v=11.2km/s=11.2×103m/s
The elastic potential energy stored in the slingshot when stretched is equal to the kinetic energy of the projectile when launched.
EPE=12kx2
where k is the spring constant and x is the stretch (2.30 m).
KE=12mv2
Setting the elastic potential energy equal to the kinetic energy:
12kx2=12mv2
We can cancel the 12 on both sides:
kx2=mv2
Rearranging the equation gives:
k=mv2x2
Substituting the values:
k=0.17kg×(11.2×103m/s)2(2.30m)2
v2=(11.2×103)2=1.2544×108m2/s2
x2=(2.30)2=5.29m2
k=0.17×1.2544×1085.29≈4.0×106N/m
Using Hooke's law, the force F required to stretch the slingshot is given by:
F=kx
Substituting the values:
F=4.0×106N/m×2.30m=9.2×106N
If one person can exert a force of 490 N, the number of people N required is:
N=FForce per person=9.2×106N490N≈18878.57
Rounding up, we find that approximately 18879 people are required to stretch the elastic bands.
Approximately 18879 people are required to stretch the elastic bands of the slingshot.
Topper's Solved these Questions
- OSCILLATIONSBOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Problems
39 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)
10 Videos
- PHOTONS AND MATTER WAVESBOOK - RESNICK AND HALLIDAYCHAPTER - PHOTONS AND MATTER WAVESEXERCISE - PRACTICE QUESTIONS(Integer Type)
4 Videos
Similar Questions
In shot putting, many athletes elect to launch the shot at an angle that is smaller than the theoretical one (about 42∘) at which the distance of a projected ball at the same speed and height is greatest. One reason has to do with the speed the athlete can give the shot during the acceleration phase of the throw. Assume that a 7.260 kg shot is acclerated along a straight path of length 1.650 m by a constant applied force of magnitude 380.0 N, starting with an initial speed of 2.500 m/s (due to the athlete's preliminary motion). What is the shot's speed at the end of the acceleration phase if the angle between the path and the horizontal is (a) 30.00∘ and (b) 42.00∘ ?
(c) By what percentage is the launch speed decreased if the athlete increases the angle from 30.00∘ to 42.00∘ ?
View SolutionA projectile is to be launched from the surface of the earth so as to escape the solar system. Consider the gravitational force on the projectile due to the earth and the sun nly. The projectile is projected perpendicular to the radius vector of the earth relative to the centre of the sun in the direction of motion of the earth. Find the minimum speed of projection relative to the earth so that the projectile escapes out of the solar system. Neglect rotation of the earth. mass if the sum Ms2×1030kg, Mass of the earth Me=6.4×1024kg Radius if the earthRe=6.4×106m, Earth- Sun distence r=1.5×1011m
View Solution
Knowledge Check
A (hypothetical) large slingshot is stretched 2.30 m to launched a 170 g projectile with speed sufficient to escape from Earth (11.2km/s). Assume the elastic bands of the slingshot obey Hooke's law.
What is the spring constant of the device if all the elastic potential energy is converted to kinetic energy?A4.03×106N/mB2.02×106N/mC8.06×106N/mD6.09×106N/mRam and Ali have been fast friends since childhood. Ali neglected studies and now has no means to earn money other than a channel whereas Ram has become an engineer. Now both are working in the same factory. Ali uses camel to transport the load within the factory.
 Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
i. The load used in each trip is 1000kg and has friction coefficient μk=0.1 and μs=0.2.
ii. Mass of camel is 500kg.
iii. Load is accelerated for first 50m with constant acceleration, then it is pulled at a constant speed of 5ms−1 for 2km and at last stopped with constant retardation in 50m.
iv. From biological data, the rate of consumption of energy of camel can be expressed as P=18×103v+104Js−1 where P is the power and v is the velocity of the camel. After calculations on different issues, Ram suggested proper food, speed of camel, etc. to his friend. For the welfare of Ali, Ram wrote a letter to the management to increase his salary.
(Assuming that the camel exerts a horizontal force on the load):
Maximum power transmitted by the camel to load isA(a) 6250Js−1B(b) 5000Js−1C(c) 105Js−1D(d) 1250Js−1When a particle is undergoing motion, the diplacement of the particle has a magnitude that is equal to or smaller than the total distance travelled by the particle. In many cases the displacement of the particle may actually be zero, while the distance travelled by it is non-zero. Both these quantities, however depend on the frame of reference in which motion of the particle is being observed. Consider a particle which is projected in the earth's gravitational field, close to its surface, with a speed of 100√2m/s, at an angle of 45∘ with the horizontal in the eastward direction. Ignore air resistance and assume that the acceleration due to gravity is 10m/s2.
Consider an observer in frame D (of the previous question), who observes a body of mass 10 kg acelerating in the upward direction at 30m/s2 (w.r.t. himself). The net force acting on this body, as observed from the ground is :-A400N in the upward directionB300N in the upward directionC200N in the upward directionD500N in the upward direction
A man can jump up to a height of h0=1m on the surface of the earth. What should be the radius of a spherical planet so that the man makes a jump on its surface and escapes out of its gravity? Assume that the man jumps with same speed as on earth and the density of planet is same as that of earth. Take escape speed on the surface of the earth to be 11.2 km/s and radius of earth to be 6400 km.
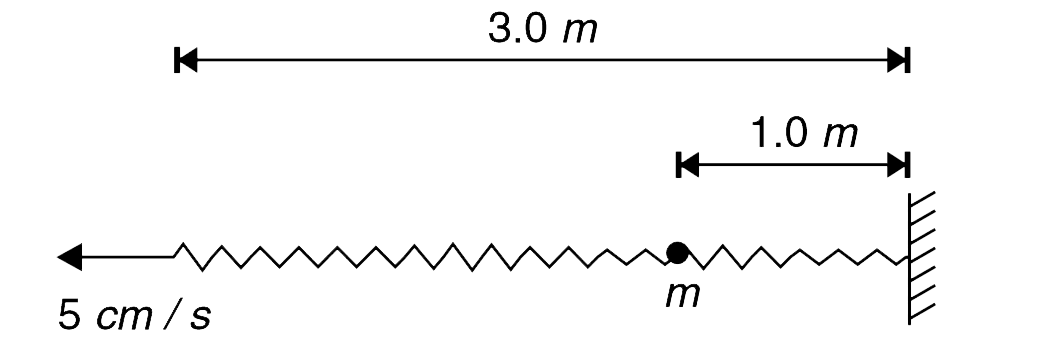
View SolutionA uniform light spring has unstretched length of 3.0 m. One of its end is fixed to a wall. A particle of mass m = 20 g is glued to the spring at a point 1.0 m away from its fixed end. The free end of the spring is pulled away from the wall at a constant speed of 5 cm/s. Assume that the spring remains horizontal (i.e., neglect gravity). Force constant of spring = 0.6 N / cm.
(a) With what speed does the particle of mass m move?
(b) Find the force applied by the external agent pulling the spring at time 2.0 s after he started pulling.
View SolutionA meteorite has mass of 500 kg and is composed of a metal. The temperature of the meteor is −20∘C and its speed is 10 km/hr when it is at large distance from a planet. The meteorite crashes into the planet and its entire kinetic energy gets converted into heat. This heat is equally shared between the planet and the meteorite. Assume that the heating of meteorite is uniform and the average specific heat capacity of the metal, for its solid, liquid and vapour phase, is 1200Jkg−1.∘C−1. The latent heat of fusion and vaporization of the metal are Lf=4×105Jkg−1 and Lv=1.1×107Jkg−1 respectively. The melting point and boiling points are 380.∘C and 2380.∘C respectively. Find the temperature of the meteorite material immediately after the impact.
Take: G=6.6×1011Nm2kg−2, mass of planet M=6×1024kg, radius of planet R = 6600 km
View SolutionRam and Ali have been fast friends since childhood. Ali neglected studies and now has no means to earn money other than a channel whereas Ram has become an engineer. Now both are working in the same factory. Ali uses camel to transport the load within the factory.
 Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
i. The load used in each trip is 1000kg and has friction coefficient μk=0.1 and μs=0.2.
ii. Mass of camel is 500kg.
iii. Load is accelerated for first 50m with constant acceleration, then it is pulled at a constant speed of 5ms−1 for 2km and at last stopped with constant retardation in 50m.
iv. From biological data, the rate of consumption of energy of camel can be expressed as P=18×103v+104Js−1 where P is the power and v is the velocity of the camel. After calculations on different issues, Ram suggested proper food, speed of camel, etc. to his friend. For the welfare of Ali, Ram wrote a letter to the management to increase his salary.
(Assuming that the camel exerts a horizontal force on the load):
The ratio of the energy consumed by the camel during uniform motion for the two cases when it moves with speed 5ms−1 to the case when it moves with 10ms−1
View SolutionRam and Ali have been fast friends since childhood. Ali neglected studies and now has no means to earn money other than a channel whereas Ram has become an engineer. Now both are working in the same factory. Ali uses camel to transport the load within the factory.
 Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
i. The load used in each trip is 1000kg and has friction coefficient μk=0.1 and μs=0.2.
ii. Mass of camel is 500kg.
iii. Load is accelerated for first 50m with constant acceleration, then it is pulled at a constant speed of 5ms−1 for 2km and at last stopped with constant retardation in 50m.
iv. From biological data, the rate of consumption of energy of camel can be expressed as P=18×103v+104Js−1 where P is the power and v is the velocity of the camel. After calculations on different issues, Ram suggested proper food, speed of camel, etc. to his friend. For the welfare of Ali, Ram wrote a letter to the management to increase his salary.
(Assuming that the camel exerts a horizontal force on the load):
The total energy consumed by the camel during the trip of 2100m is
View Solution
