A block weighing 10.0 N is attached to the lower end of a verticle spring (k=200.0N/m), the other end of which is attached to a ceiling. The block oscillates vertically and has a kinetic energy of 2.00 J as it passes through the point at which the spring is unstretched.
What is the amplitude of the oscillation and the maximum kinetic energy of the block as it oscillates?
0.20 m and 4.50 J
0.30 m and 3.35 J
0.25 m and 3.25 J
0.15 m and 2.25 J
The correct Answer is:D
To solve the problem step by step, we will break it down into two parts: finding the amplitude of the oscillation and the maximum kinetic energy of the block.
Step 1: Determine the Extension of the Spring at Equilibrium
When the block is attached to the spring, it stretches the spring until it reaches an equilibrium position. At this point, the force exerted by the spring equals the weight of the block.
- Given:
- Weight of the block (W) = 10.0 N
- Spring constant (k) = 200.0 N/m
Using Hooke's Law, the force exerted by the spring can be expressed as:
Fspring=k⋅x
Where x is the extension of the spring.
At equilibrium:
W=Fspring
10.0=200.0⋅x
Solving for x:
x=10.0200.0=0.05m
Step 2: Calculate Total Energy at the Unstretched Position
When the block passes through the point where the spring is unstretched, it has a kinetic energy of 2.00 J. At this point, the potential energy is zero because the spring is unstretched.
The total mechanical energy (E) in the system is given by:
E=K+U
Where K is the kinetic energy and U is the potential energy.
At the unstretched position:
E=2.00+0=2.00J
Step 3: Calculate the Total Energy at Maximum Displacement (Amplitude)
At the maximum displacement (amplitude A), the kinetic energy is zero, and all the energy is potential energy:
E=U=12kA2
Setting the total energy equal to the potential energy at maximum displacement:
2.00=12⋅200.0⋅A2
Solving for A2:
2.00=100.0⋅A2
A2=2.00100.0=0.02
A=√0.02=0.1414m
Step 4: Calculate Maximum Kinetic Energy
The maximum kinetic energy occurs when the block is at the equilibrium position. At this point, all the total energy is kinetic energy:
Kmax=E=2.00J
Final Results
- Amplitude of the oscillation: A≈0.1414m
- Maximum kinetic energy: Kmax=2.00J
When the block is attached to the spring, it stretches the spring until it reaches an equilibrium position. At this point, the force exerted by the spring equals the weight of the block.
- Weight of the block (W) = 10.0 N
- Spring constant (k) = 200.0 N/m
Fspring=k⋅x
Where x is the extension of the spring.
W=Fspring
10.0=200.0⋅x
x=10.0200.0=0.05m
When the block passes through the point where the spring is unstretched, it has a kinetic energy of 2.00 J. At this point, the potential energy is zero because the spring is unstretched.
E=K+U
Where K is the kinetic energy and U is the potential energy.
E=2.00+0=2.00J
At the maximum displacement (amplitude A), the kinetic energy is zero, and all the energy is potential energy:
E=U=12kA2
2.00=12⋅200.0⋅A2
2.00=100.0⋅A2
A2=2.00100.0=0.02
A=√0.02=0.1414m
The maximum kinetic energy occurs when the block is at the equilibrium position. At this point, all the total energy is kinetic energy:
Kmax=E=2.00J
- Amplitude of the oscillation: A≈0.1414m
- Maximum kinetic energy: Kmax=2.00J
Topper's Solved these Questions
- OSCILLATIONSBOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Problems
39 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)
10 Videos
- PHOTONS AND MATTER WAVESBOOK - RESNICK AND HALLIDAYCHAPTER - PHOTONS AND MATTER WAVESEXERCISE - PRACTICE QUESTIONS(Integer Type)
4 Videos
Similar Questions
A block weighing 10N is attached to the lower end of a vertical spring (k =200N/m), the other end of which is attached to a ceiling. The block oscillates vertically and has a kinetic energy of 2.0J as it passes through the point at which the spring is unstretched. The amplitude of the oscillation of block is
View SolutionA large fake cookie sliding on a horizontal surface is attached to one end of a horizontal spring with spring constant k=360 N/m, the other end of the spring is fixed in place. The cookie has a kinetic energy of 20.0 J as it passes through the spring's equilibrium position. As the cookie slides, a frictional force of magnitude 10.0 N acts on it . (a) How far will the cookie slide from the equilibrium position before coming momentarily to rest ? (c) What will be the kinetic energy of the cookie as it slides back through the equilibrium position ?
View Solution
Knowledge Check
A block weighing 10.0 N is attached to the lower end of a verticle spring (k=200.0N/m), the other end of which is attached to a ceiling. The block oscillates vertically and has a kinetic energy of 2.00 J as it passes through the point at which the spring is unstretched.
What is the period of the oscillation?A0.45 sB0.90 sC0.15 sD0.303 sA block weighing 10.0 N is attached to the lower end of a verticle spring (k=200.0N/m), the other end of which is attached to a ceiling. The block oscillates vertically and has a kinetic energy of 2.00 J as it passes through the point at which the spring is unstretched.
Use the law of conservation of energy to determine the maximum distance the block moves both above and below the point at which the spring is unstretched (these are not necessarily the same)A0.05 m and 0.25 mB0.1. m and 0.20 mC0.15 m and 0.15 mD0.13 m and 0.17 mA block of mass m lies on a horizontal frictionless surface and is attached to one end of a horizontal spring (with spring constant k) whose other end is fixed . The block is intinally at rest at the position where the spring is unstretched (x=0). When a constant horizontal force →F in the positive direction of the x−axis is applied to it, a plot of the resulting kinetic energy of the block versus its position x is shown in figure. What is the magnitude of →F ?
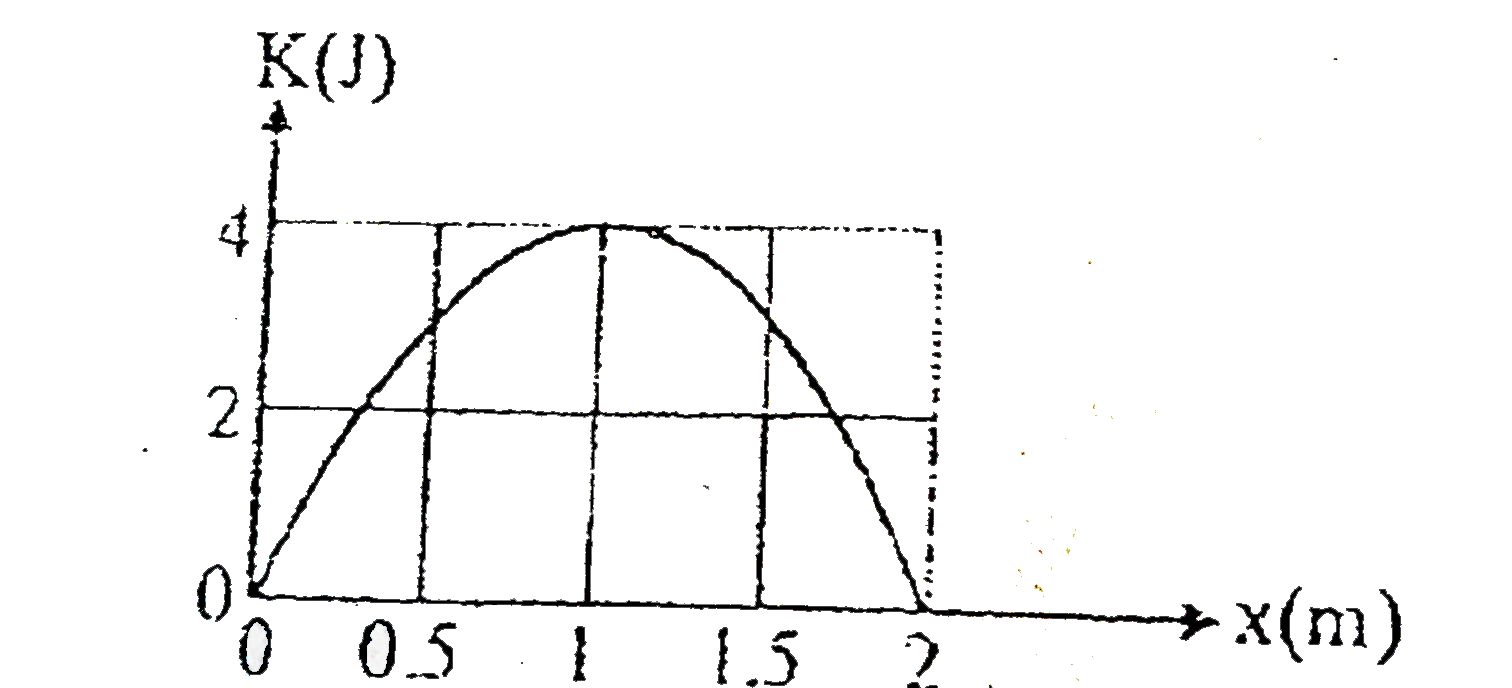 A2NB4NC8ND16N
A2NB4NC8ND16N
A block of mass m lies on a horizontal frictionless surface and is attached to one end of a horizontal spring (with spring constant k) whose other end is fixed . The block is intinally at rest at the position where the spring is unstretched (x=0). When a costant horizontal force →F in the positive direction of the x−axis is applied to it, a plot of the resulting kinetic energy of the block verus its position x is shown in figure. What is the magnitude of →F
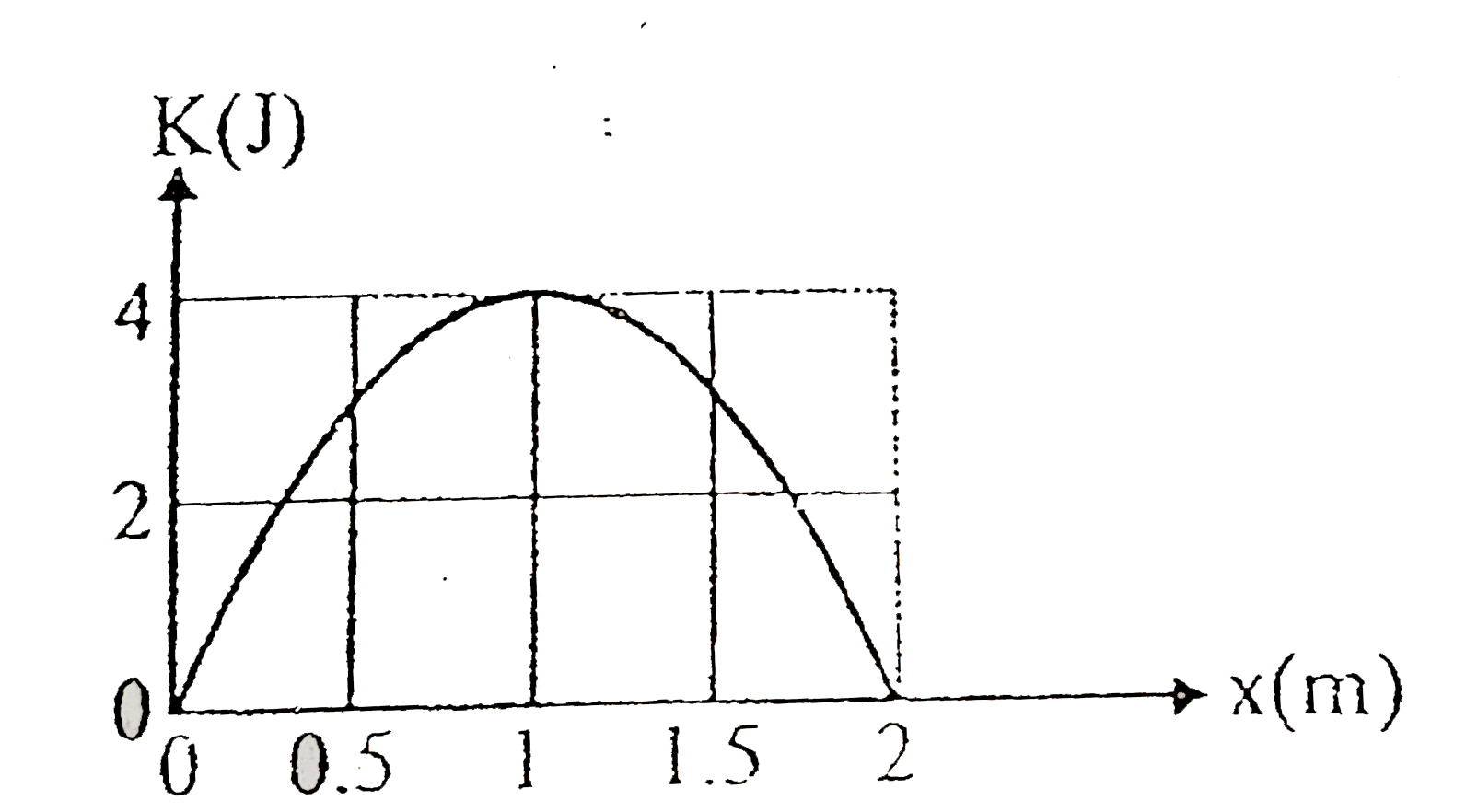
View SolutionIn a horizontal spring-block system force constant of spring is k = 16N/m, mass of the block is 1 kg. Maximum kinetic energy of the block is 8J. Then
View SolutionWhen a mass M is attached to the spring of force constant k , then the spring stretches by . If the mass oscillates with amplitude l , what will be maximum potential energy stored in the spring
View SolutionA 0.25kg block oscillates on the end of the spring with a spring constant of 200N/m. If the oscillation is started by elongating the spring 0.15m and giving the block a speed of 3.0m/s, then the maximum speed of the block is
View SolutionA spring has natural length 40cm and spring constant 500N/m. A block of mass 1kg is attached at one end of the spring and other end of the spring is attached to a ceiling. The block is relesed from the position, where the spring has length 45cm.
View Solution
