A steel rod of length . has a cross sectional area A. The force required to stretch this rod by the same amount as the expansion produced by heating it through is (coefficient of linear expansion of steel is and young's modulus for steel is Y ).
The correct Answer is:A
To solve the problem of finding the force required to stretch a steel rod by the same amount as the expansion produced by heating it through a temperature change ΔT, we can follow these steps:
1. Understand the Expansion Due to Heating:
The change in length (ΔL) of the steel rod when heated can be expressed using the coefficient of linear expansion (α):
ΔL=L0⋅α⋅ΔT
where L0 is the original length of the rod.
2. Define Strain:
Strain (ϵ) is defined as the change in length divided by the original length:
ϵ=ΔLL0=L0⋅α⋅ΔTL0=α⋅ΔT
3. Define Stress:
Stress (σ) is related to strain through Young's modulus (Y):
σ=Y⋅ϵ
Substituting the expression for strain:
σ=Y⋅(α⋅ΔT)
4. Relate Stress to Force:
Stress is also defined as force (F) per unit area (A):
σ=FA
Therefore, we can express force in terms of stress:
F=σ⋅A
5. Combine the Equations:
Substitute the expression for stress into the force equation:
F=(Y⋅(α⋅ΔT))⋅A
This simplifies to:
F=Y⋅α⋅ΔT⋅A
Final Expression
Thus, the force required to stretch the steel rod by the same amount as the expansion produced by heating it through ΔT is given by:
F=Y⋅α⋅ΔT⋅A
The change in length (ΔL) of the steel rod when heated can be expressed using the coefficient of linear expansion (α):
ΔL=L0⋅α⋅ΔT
where L0 is the original length of the rod.
Strain (ϵ) is defined as the change in length divided by the original length:
ϵ=ΔLL0=L0⋅α⋅ΔTL0=α⋅ΔT
Stress (σ) is related to strain through Young's modulus (Y):
σ=Y⋅ϵ
Substituting the expression for strain:
σ=Y⋅(α⋅ΔT)
Stress is also defined as force (F) per unit area (A):
σ=FA
Therefore, we can express force in terms of stress:
F=σ⋅A
Substitute the expression for stress into the force equation:
F=(Y⋅(α⋅ΔT))⋅A
This simplifies to:
F=Y⋅α⋅ΔT⋅A
Thus, the force required to stretch the steel rod by the same amount as the expansion produced by heating it through ΔT is given by:
F=Y⋅α⋅ΔT⋅A
Topper's Solved these Questions
- TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION BOOK - RESNICK AND HALLIDAYCHAPTER - TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION EXERCISE - PRACTICE QUETIONS (More than One Correct Choice Type )
7 Videos
- TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION BOOK - RESNICK AND HALLIDAYCHAPTER - TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION EXERCISE - PRACTICE QUETIONS (Matrix- Match )
3 Videos
- TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION BOOK - RESNICK AND HALLIDAYCHAPTER - TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION EXERCISE - PROBLEMS
24 Videos
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)
2 Videos
- THE FIRST LAW OF THERMODYNAMICSBOOK - RESNICK AND HALLIDAYCHAPTER - THE FIRST LAW OF THERMODYNAMICSEXERCISE - PRACTICE QUESTIONS ( INTEGER TYPE )
3 Videos
Similar Questions
A steel rod 25 cm long has a cross -sectiional area of 0.8cm2. What force wouyld be required to stretch this rod by the same amount as the expansion produced by heating it by 10∘C? Given that for steel coefficient of linear expansion and Young's modulus are given as α=1.1×10−5.∘C−1 and Y=2×1011Nm−2
View SolutionA steel rod of length 50 cm has a cross–sectional area of 0.4cm2. What force would be required to stretch this rod by the same amount as the expansion produced by heating it through 10∘C .
(α=10−5k−1 and Y=2×1011N/m2)
View Solution
Knowledge Check
A steel rod of length 25cm has a cross-sectional area of 0.8cm2 . The force required to stretch this rod by the same amount as the expansion produced by heating it through 10∘C is (αsteel=10−5/∘C and Ysteel=2×1010N/m2)
A40NB80NC120ND160NA metal rod of length 'L' and cross-sectional area 'A' is heated through 'T'∘C What is the force required to prevent the expansion of the rod lengthwise ?
AYAαT(1−αT)BYAαT(1+αT)C(1−αT)YAαTD(1+αT)YAαTCalculate the compressional force required to prevent the metallic rod of length l cm and cross sectional area Acm2 when heated through t∘C from expanding lengthwise. Young's modulus of elasticity of the metal is E and mean coefficient of linear expansion is α per degree celsius.
AEAαtBEAαt/((1+αt)CEAαt/(1−at)DElαt

In figure which strip (brass or steel) has higher coefficient of linear expansion.
View SolutionTwo steel rods and an aluminium rod of equal length l0 and equal cross section are joined rigidly at their ends as shown in the figure below. All the rods are in a state of zero tension at 00C. Find the length of the system when the temperature is raised to θ. Coefficient of linear expansion of aluminium and steel are αaandαs respectively. Young's modulus of aluminium is Ya and of steel is Ys.
steel
Aluminium
Steel

View SolutionTwo same length rods of brass and steel of equal cross-sectional area are joined end to end as shown in figure and supported between two rigid vertical walls. Initially the rods are unstrained. If the temperature of system is raised by Δt. Find the displacement of the junction of two rods. Given that the coefficient of linear expansion and young's modulus of brass and steel are aphab.αs(αb>αs),Yb and Ys respectively.
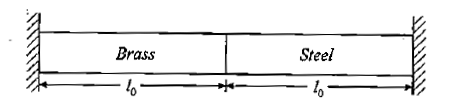
View SolutionCalculate the compressional force required to prevent the metallic rod length lcm and cross-sectional area Acm2 when heated through t∘C, from expanding along length wise. The Young's modulus of elasticity of the metal is E and mean coefficient of linear expansion is α per degree Celsius
View SolutionCalculate the compressional force required to prevent the metallic rod length lcm and cross-sectional area Acm2 when heated through t∘C, from expanding along length wise. The Young's modulus of elasticity of the metal is E and mean coefficient of linear expansion is α per degree Celsiuss
View Solution
