The ends of a thin bar are maintained at different temperatures. The temperature of the cooler end is , while the temperature at a point 0.13m from the cooler end is and the temperature of the warmer end is . Assuming that heat flows only along the length of the bar ( the sides are insulated), find the length of the bar.
0.50m
0.40m
0.23m
0.64m
The correct Answer is:B
To solve the problem, we will use the concept of heat conduction along the bar and apply the principle that the rate of heat flow is the same throughout the bar.
1. Identify the given temperatures and distances:
- Cooler end temperature, T1=11∘C
- Temperature at a point 0.13m from the cooler end, T2=23∘C
- Warmer end temperature, T3=48∘C
- Distance from the cooler end to the point where temperature is 23∘C, d1=0.13m
2. Define the length of the bar:
- Let the total length of the bar be L.
- The length from the cooler end to the point where the temperature is 23∘C is d1=0.13m.
- The remaining length from this point to the warmer end is d2=L−0.13.
3. Set up the heat conduction equations:
- According to Fourier's law of heat conduction, the heat flow rate Q is given by:
Q=K⋅A⋅(T2−T1)d1=K⋅A⋅(T3−T2)d2
- Here, K is the thermal conductivity, and A is the cross-sectional area of the bar.
4. Substitute the known values:
- For the first segment (from cooler end to point at 23∘C):
Q=K⋅A⋅(23−11)0.13=K⋅A⋅120.13
- For the second segment (from point at 23∘C to warmer end):
Q=K⋅A⋅(48−23)d2=K⋅A⋅25d2
5. Equate the two expressions for Q:
K⋅A⋅120.13=K⋅A⋅25d2
- Cancel K and A from both sides:
120.13=25d2
6. Solve for d2:
d2=25⋅0.1312
d2=3.2512≈0.2708m
7. Calculate the total length L:
L=d1+d2=0.13+0.2708≈0.4008m
- Rounding to two decimal places, we find:
L≈0.40m
Final Answer:
The total length of the bar is approximately 0.40m.
- Cooler end temperature, T1=11∘C
- Temperature at a point 0.13m from the cooler end, T2=23∘C
- Warmer end temperature, T3=48∘C
- Distance from the cooler end to the point where temperature is 23∘C, d1=0.13m
- Let the total length of the bar be L.
- The length from the cooler end to the point where the temperature is 23∘C is d1=0.13m.
- The remaining length from this point to the warmer end is d2=L−0.13.
- According to Fourier's law of heat conduction, the heat flow rate Q is given by:
Q=K⋅A⋅(T2−T1)d1=K⋅A⋅(T3−T2)d2
- Here, K is the thermal conductivity, and A is the cross-sectional area of the bar.
- For the first segment (from cooler end to point at 23∘C):
Q=K⋅A⋅(23−11)0.13=K⋅A⋅120.13
- For the second segment (from point at 23∘C to warmer end):
Q=K⋅A⋅(48−23)d2=K⋅A⋅25d2
K⋅A⋅120.13=K⋅A⋅25d2
- Cancel K and A from both sides:
120.13=25d2
d2=25⋅0.1312
d2=3.2512≈0.2708m
L=d1+d2=0.13+0.2708≈0.4008m
- Rounding to two decimal places, we find:
L≈0.40m
The total length of the bar is approximately 0.40m.
Topper's Solved these Questions
- HEAT-MEASUREMENT AND TRANSFERBook:RESNICK AND HALLIDAYChapter:HEAT-MEASUREMENT AND TRANSFERExercise:PRACTICE QUESTIONS(MORE THAN ONE CORRECT CHOICE TYPE )
Explore 8 Videos
- HEAT-MEASUREMENT AND TRANSFERBook:RESNICK AND HALLIDAYChapter:HEAT-MEASUREMENT AND TRANSFERExercise:PRACTICE QUESTIONS( LINKED COMPREHENSION)
Explore 9 Videos
- HEAT-MEASUREMENT AND TRANSFERBook:RESNICK AND HALLIDAYChapter:HEAT-MEASUREMENT AND TRANSFERExercise:PROBLEMS
Explore 35 Videos
- GRAVITATIONBook:RESNICK AND HALLIDAYChapter:GRAVITATIONExercise:PRACTICE QUESTIONS (INTEGER TYPE)
Explore 4 Videos
- HYDROGEN ATOMBook:RESNICK AND HALLIDAYChapter:HYDROGEN ATOMExercise:PRACTICE QUESTIONS(Integer Type)
Explore 6 Videos
Similar Questions
The temperature gradient in a rod 0.5 m long is 40∘C per metre. The temperature of the hotter end is 30∘C. What is the temperature of its colder end?
View SolutionThe temperature gradient in a rod of 1m long is '100^@' C/m if the temperature of hotter end is '30^@' C, then the temperature of colder end is
View Solution
Knowledge Check
The temperature gradient in a rod of 0.5m length is 80∘C/m. It the temperature of hotter end of the rod is 30∘C, then the temperature of the cooler end is
A40∘CB−10∘CC10∘CD0∘CThe temperature gradient in a rod of 0.5 m long is 80∘C/m. If the temperature of hotter end of the rod is 30∘C, then the temperature of the colder end is
A40∘CB−10∘CC10∘CD0∘CWhen two ends of a rod wrapped with cotton are maintained at different temperatures and after some time every point of the rod attains a constant temperature, then
AConduction of heat at different points of the rod stops because the temperature is not increasingBRod is bad conductor of heatCHeat is being radiated from each point of the rodDEach point of the rod is giving heat to its neighbour at the same rate at which it is receiving heat
The ends of a metallic bar are maintained at different temperature and there is no loss/gain of heat from the sides of the bar due to conduction or radiation. In the steady state the temperature variation along the length of the bar is a shown in the figure what do you think about the cross sectional area of the bar?
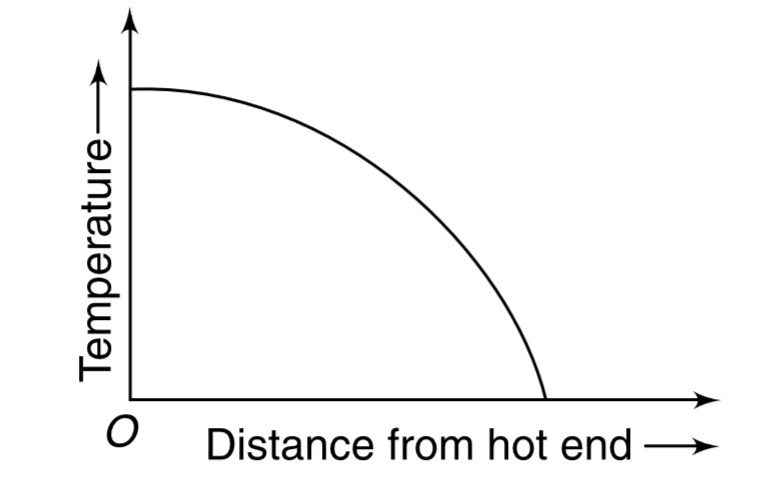
View SolutionIn the steady state the two ends of a meter rod are at 30∘C and 20∘C the temperature at the 40thcm from the end at higher temperature is .
View SolutionThe two ends of a metal rod are maintained at temperatures 100∘C and 110∘C . The rate of heat flow in the rod is found to be 4.0j/s. If the ends are maintaind at temperatures 200∘C and 210∘C, the rate of heat flow will be :
View SolutionThe two ends of a metal rod are maintained at temperatures 100∘C and 110∘C . The rate of heat flow in the rod is found to be 4.0j/s. If the ends are maintaind at temperatures 200∘C and 210∘C, the rate of heat flow will be :
View SolutionIn a steady state of heat conduction the temperature of the ends A and B of a rod 100cm long per 0∘C and 100∘C The temperature of the rod at a point 60cm distant from the end A is .
View Solution