A thermally isolated sample of an ideal gas at a fixed temperature is confined to one half of a container by an impermeable membrane. The other half of the container is evacuated. The membrane is then pierced and the gas is allowed to expand freely and to double its volume as shown. Which one of the following statements is true concerning this situation?
The process is reversible.
This is an isothermal process.
The entropy of the gas decreases.
The internal energy of the gas must decrease.
The correct Answer is:B
To solve the problem step by step, let's analyze the situation described:
Step 1: Understand the Initial Conditions
- We have a thermally isolated container divided by an impermeable membrane.
- One half of the container contains an ideal gas at a fixed temperature, while the other half is a vacuum (evacuated).
- The initial volume of the gas is V0 (in one half of the container).
Hint: Identify the properties of the system, including the fact that it is thermally isolated and that one side is a vacuum.
Step 2: Analyze the Process of Expansion
- When the membrane is pierced, the gas expands freely into the vacuum.
- This is a free expansion process, meaning there is no external pressure opposing the expansion.
Hint: Recall that free expansion occurs when a gas expands into a vacuum, resulting in no work done against external pressure.
Step 3: Apply the First Law of Thermodynamics
- The First Law of Thermodynamics states:
ΔQ=ΔU+W
where ΔQ is the heat added to the system, ΔU is the change in internal energy, and W is the work done by the system.
- Since the system is thermally isolated, ΔQ=0.
- The work done by the gas during free expansion into a vacuum is also W=0.
Hint: Remember that in an isolated system, no heat is exchanged with the surroundings, and in free expansion, no work is done.
Step 4: Determine the Change in Internal Energy
- From the First Law, we have:
0=ΔU+0⟹ΔU=0
- The change in internal energy ΔU being zero indicates that the internal energy of the gas remains constant.
Hint: Consider that for an ideal gas, the internal energy is a function of temperature. If ΔU=0, then the temperature must also remain constant.
Step 5: Identify the Type of Process
- Since the temperature remains constant during the expansion, this process is classified as an isothermal process.
- Additionally, because the gas expands into a vacuum, this process is irreversible.
Hint: Isothermal processes occur at constant temperature, and free expansion is inherently irreversible.
Step 6: Evaluate the Statements
Now, we can evaluate the statements provided in the question:
1. The process is isothermal (True).
2. The process is reversible (False).
3. The entropy of the system decreases (False).
4. The internal energy of the gas decreases (False).
Hint: Analyze each statement based on the conclusions drawn from the analysis of the process.
Conclusion
The correct statement concerning the situation is that the process is isothermal.
- We have a thermally isolated container divided by an impermeable membrane.
- One half of the container contains an ideal gas at a fixed temperature, while the other half is a vacuum (evacuated).
- The initial volume of the gas is V0 (in one half of the container).
- When the membrane is pierced, the gas expands freely into the vacuum.
- This is a free expansion process, meaning there is no external pressure opposing the expansion.
- The First Law of Thermodynamics states:
ΔQ=ΔU+W
where ΔQ is the heat added to the system, ΔU is the change in internal energy, and W is the work done by the system.
- Since the system is thermally isolated, ΔQ=0.
- The work done by the gas during free expansion into a vacuum is also W=0.
- From the First Law, we have:
0=ΔU+0⟹ΔU=0
- The change in internal energy ΔU being zero indicates that the internal energy of the gas remains constant.
- Since the temperature remains constant during the expansion, this process is classified as an isothermal process.
- Additionally, because the gas expands into a vacuum, this process is irreversible.
Now, we can evaluate the statements provided in the question:
1. The process is isothermal (True).
2. The process is reversible (False).
3. The entropy of the system decreases (False).
4. The internal energy of the gas decreases (False).
The correct statement concerning the situation is that the process is isothermal.
Topper's Solved these Questions
- THE FIRST LAW OF THERMODYNAMICSBOOK - RESNICK AND HALLIDAYCHAPTER - THE FIRST LAW OF THERMODYNAMICSEXERCISE - PRACTICE QUESTIONS ( MORE THAN ONE CORRECT CHOICE TYPE )
9 Videos
- THE FIRST LAW OF THERMODYNAMICSBOOK - RESNICK AND HALLIDAYCHAPTER - THE FIRST LAW OF THERMODYNAMICSEXERCISE - PRACTICE QUESTIONS ( LINKED COMPREHENSION )
15 Videos
- THE FIRST LAW OF THERMODYNAMICSBOOK - RESNICK AND HALLIDAYCHAPTER - THE FIRST LAW OF THERMODYNAMICSEXERCISE - PROBLEMS
41 Videos
- TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION BOOK - RESNICK AND HALLIDAYCHAPTER - TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION EXERCISE - PRACTICE QUETIONS (Integer Type)
4 Videos
- THE KINETIC THEORY OF GASESBOOK - RESNICK AND HALLIDAYCHAPTER - THE KINETIC THEORY OF GASESEXERCISE - PRACTICE QUESTIONS
72 Videos
Similar Questions
A closed container is fully insulated from outside. One half of it is filled with an ideal gas X separated by a plate P from the other half Y which contains a vacuum as shown in figure. When P is removed, X moves into Y. Which of the following statements is correct ?

View SolutionOne mole ofan ideal gas is allowed to expand freely and adiabatically into vacuum until its volume has doubled. The expression which is not true concerning statement is
View Solution
Knowledge Check
An ideal gas is heated at constant volume until its pressure doubles. Which one of the following statements is correct?
AThe mean speed of the molecule doubles.BThe number of molecules doubles.CThe mean square speed of the molecules doubles.DThe number of molecules per unit volume doubles.One mole of an ideal gas is allowed to expand freely and adiabatically into vacuum until its volume has doubled. A statement which is not true concerning this expression is
AΔH=0BΔS=0CΔE=0DW = 0One mole of an ideal gas is taken through a cyclic process as shown in the V-T diagram. Which of the following statements is true ?
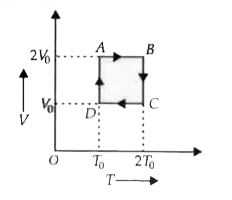 AThe magnitude of work done by the gas is RT0ln2.BWork done by gas is V0T0CNet work done by the gas is zero.DWork done by the gas is 2RT0ln2.
AThe magnitude of work done by the gas is RT0ln2.BWork done by gas is V0T0CNet work done by the gas is zero.DWork done by the gas is 2RT0ln2.
Mixing of N2 and H2 form an ideal gas mixture at roo, temperature in a container.For this process, which of the following statements is true?
View SolutionWhich one of the following statements concerning a collection of gas molecules at a certain temperature is true?
View Solution_E01_097_Q01.png)
Three blocks, labeled A, B and C are floating in water as shown in the drawing blocks A and B have the same mass and volume Block C has the same volume but is submerged to a greater depth that the other two blocks which one of the following statements concerning this situation is/are true?
View SolutionTwo flasks A and B of equal capacity of volume contain SO3 and CO gas respectively under similar conditions of temperature and pressure. Then, which of the following statement is true?
View SolutionWhen a sample of ideal gas is changed from an initial state to a final state, various curves can be plotted for the process like P-V curve, V-T curve,P-T curve etc.
For example, P-V curve for a fixed amount of an ideal gas at constant temperature is a rectangular hyperbola, V-T curve for a fixed amount of an ideal gas at constant volume is again a straight line. However, the shapes may vary if the constant parameters are also changed.
Now, answer the following questions :
Which of the following statements is correct regarding a fixed amount of ideal gas undergoing the following process :
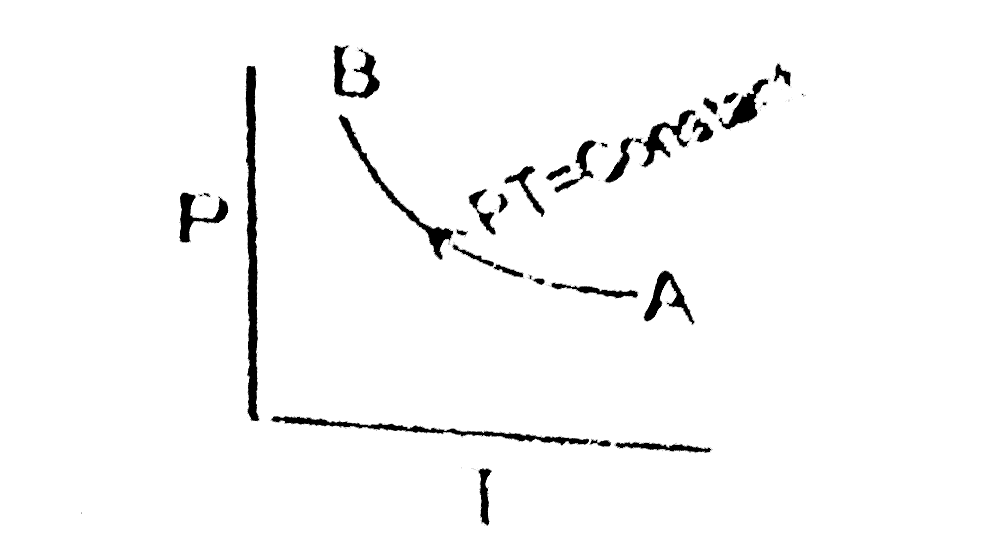
View Solution
