Suppose a monatomic ideal gas is contained within a vertical cylinder that is fitted with a movable piston. The piston is frictionless and has a negligible mass. The area of the piston is3.14×10−2m2, and the pressure outside the cylinder is 1.01×105 Pa. Heat (2093 J) is removed from the gas. Through what distance does the piston drop?
0.185m
0.389m
0.539m
0.264m
The correct Answer is:D
To solve the problem, we need to determine the distance the piston drops when 2093 J of heat is removed from a monatomic ideal gas in a cylinder. We will use the first law of thermodynamics and the relationship between pressure, area, and displacement.
1. Identify the Given Data:
- Area of the piston, A=3.14×10−2m2
- External pressure, P=1.01×105Pa
- Heat removed from the gas, Q=−2093J (negative because heat is removed)
2. Understand the First Law of Thermodynamics:
The first law states:
ΔU=Q+W
where ΔU is the change in internal energy, Q is the heat added to the system, and W is the work done by the system. Since heat is removed, Q is negative.
3. Calculate Work Done by the Gas:
At constant pressure, the work done by the gas when the piston moves down is given by:
W=PΔV
where ΔV is the change in volume. The change in volume can also be expressed in terms of the area of the piston and the distance it moves down:
ΔV=A⋅x
where x is the distance the piston drops.
4. Substituting Work into the First Law:
Rearranging the first law gives:
ΔU=Q+PΔV
Substituting for ΔV:
ΔU=Q+P(A⋅x)
5. Relate Change in Internal Energy to Heat Removed:
For a monatomic ideal gas, the change in internal energy can be expressed as:
ΔU=32nRΔT
However, since we are not given the number of moles or temperature change directly, we will use the heat removed directly in our calculations.
6. Setting Up the Equation:
From the first law:
−2093=P(A⋅x)
Rearranging gives:
x=−2093P⋅A
7. Substituting Values:
Substitute the values for P and A:
x=−2093(1.01×105)⋅(3.14×10−2)
8. Calculating x:
x=−2093(1.01×105)⋅(3.14×10−2)≈−20933164.14≈−0.661m
Since we are interested in the distance the piston drops, we take the absolute value:
x≈0.661m
Final Answer:
The piston drops approximately 0.661 meters.
- Area of the piston, A=3.14×10−2m2
- External pressure, P=1.01×105Pa
- Heat removed from the gas, Q=−2093J (negative because heat is removed)
The first law states:
ΔU=Q+W
where ΔU is the change in internal energy, Q is the heat added to the system, and W is the work done by the system. Since heat is removed, Q is negative.
At constant pressure, the work done by the gas when the piston moves down is given by:
W=PΔV
where ΔV is the change in volume. The change in volume can also be expressed in terms of the area of the piston and the distance it moves down:
ΔV=A⋅x
where x is the distance the piston drops.
Rearranging the first law gives:
ΔU=Q+PΔV
Substituting for ΔV:
ΔU=Q+P(A⋅x)
For a monatomic ideal gas, the change in internal energy can be expressed as:
ΔU=32nRΔT
However, since we are not given the number of moles or temperature change directly, we will use the heat removed directly in our calculations.
From the first law:
−2093=P(A⋅x)
Rearranging gives:
x=−2093P⋅A
Substitute the values for P and A:
x=−2093(1.01×105)⋅(3.14×10−2)
x=−2093(1.01×105)⋅(3.14×10−2)≈−20933164.14≈−0.661m
x≈0.661m
The piston drops approximately 0.661 meters.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - THE FIRST LAW OF THERMODYNAMICSEXERCISE - PRACTICE QUESTIONS ( MORE THAN ONE CORRECT CHOICE TYPE )9videos
THE FIRST LAW OF THERMODYNAMICS
- BOOK - RESNICK AND HALLIDAYCHAPTER - THE FIRST LAW OF THERMODYNAMICSEXERCISE - PRACTICE QUESTIONS ( LINKED COMPREHENSION )15videos
THE FIRST LAW OF THERMODYNAMICS
- BOOK - RESNICK AND HALLIDAYCHAPTER - THE FIRST LAW OF THERMODYNAMICSEXERCISE - PROBLEMS41videos
THE FIRST LAW OF THERMODYNAMICS
- BOOK - RESNICK AND HALLIDAYCHAPTER - TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION EXERCISE - PRACTICE QUETIONS (Integer Type)4videos
TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION
- BOOK - RESNICK AND HALLIDAYCHAPTER - THE KINETIC THEORY OF GASESEXERCISE - PRACTICE QUESTIONS72videos
THE KINETIC THEORY OF GASES
Similar Questions
Ten dm3 of hydrogen under 1 bar pressure are contained in a cylinder which has a movable piston. The piston is moved in until the same mass of gas occupies 2dm3 at the same temperature. Find the pressure in the cylinder.
View SolutionThe pressure of a gas contained in a cylinder with a movable piston is 300 Pa. The area of the piston is 0.5m2. Calculate the force that is exerted on the piston.
View Solution
Knowledge Check
- Question 1 - Select One
A gas is contained in a metallic cylinder fitted with a piston.The piston is suddenly moved in to compress the gas and is maintained at this position. As time passes the pressure of the gas in the cylinder
AincreasesBDecreasesCRemans constantDIncreases or decreases depending on the nature of the gas. - Question 2 - Select One
A gas is contained in a metallic cylinder fitted with a piston.the piston is suddenly moved in to compress the gas and is maintained at this position. As time passes the pressure of the gas in the cylinder
AincreaseBdecreaseCremains constantDincrease or decrease depending on the nature of the gas. - Question 3 - Select One
10dm3 of hydrogen under 1 bar pressure are contained in a cylinder which has a movable piston. The piston is moved in until the same mass of gas occupies 2dm3 at the same temperature. What will be the pressure in the cylinder ?
A5 barB6 barC7 barDNone of these
Two moles of an ideal monoatomic gas are confined within a cylinder by a massless spring loaded with a frictionless piston of negligible mass and of cross-sectional area 4×10−3m2. The springis initially in its relaxed state. Now the gas is heated by a heater for some time. During this time the gas expands and does 50 J of work in moving the piston through a distance of 0.1 m. The temperature of the gas increases by 50 K. Calculate the spring constant and the heat supplied by the heater.
View SolutionAn ideal gas enclosed in a cylinder fitted with a frictionless and weightless piston, pushes it outside. What would be the sign convention for the work ?
View SolutionTwo mole of an ideal monatomic gas are confined within a cylinder by a mass less spring loaded with a frictionless piston of negligible mass and crossectional area 4×10−3m2. The gas is heated by a heater for some time. During this time the gas expands and does 50J of work in moving the piston through a distance of 0.01m. The temperature of gas increases by 50k.
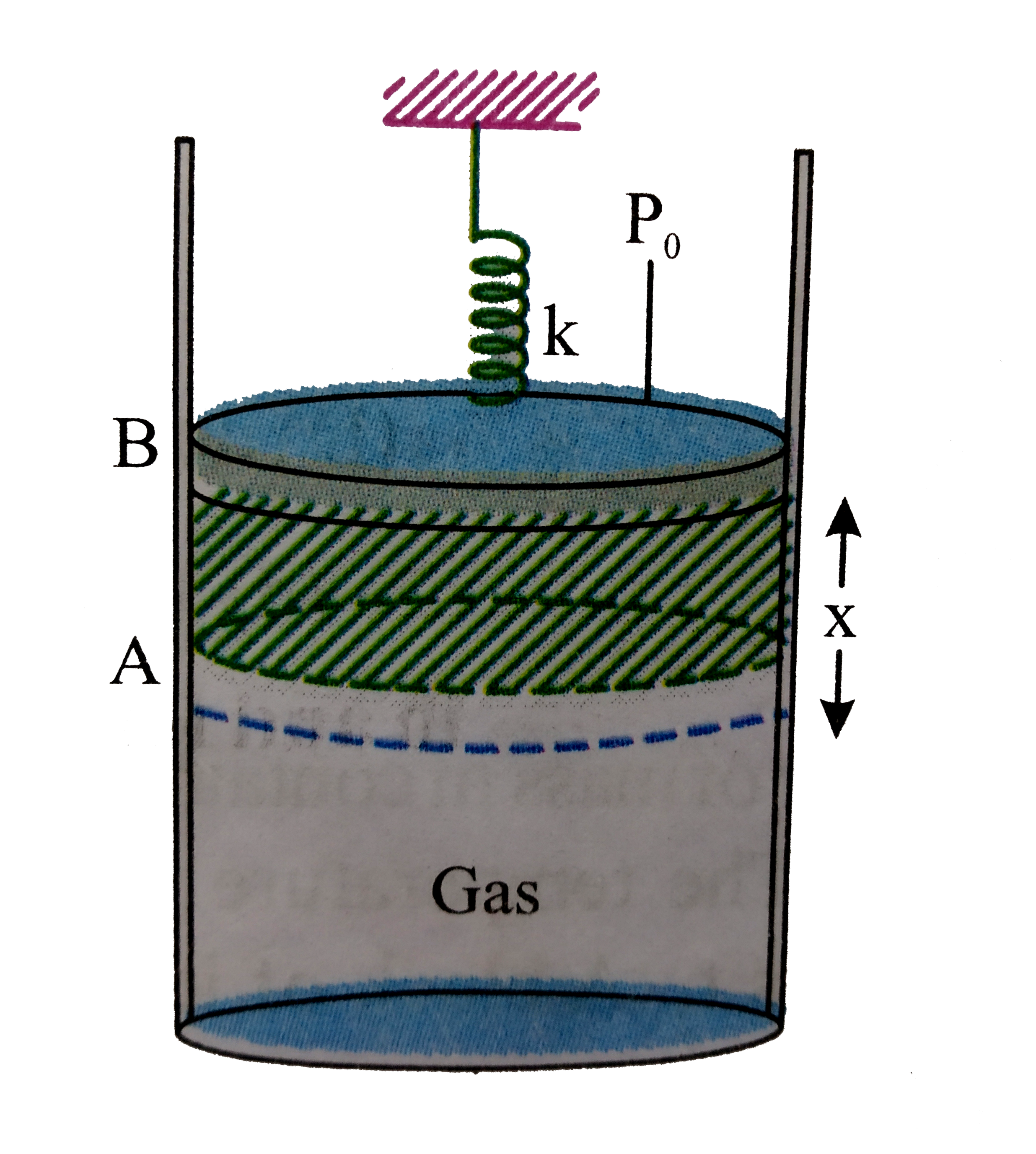
Heat supplied by heater during this process isView SolutionTwo mole of an ideal monatomic gas are confined within a cylinder by a mass less spring loaded with a frictionless piston of negligible mass and crossectional area 4×10−3m2. The gas is heated by a heater for some time. During this time the gas expands and does 50J of work in moving the piston through a distance of 0.01m. The temperature of gas increases by 50k.
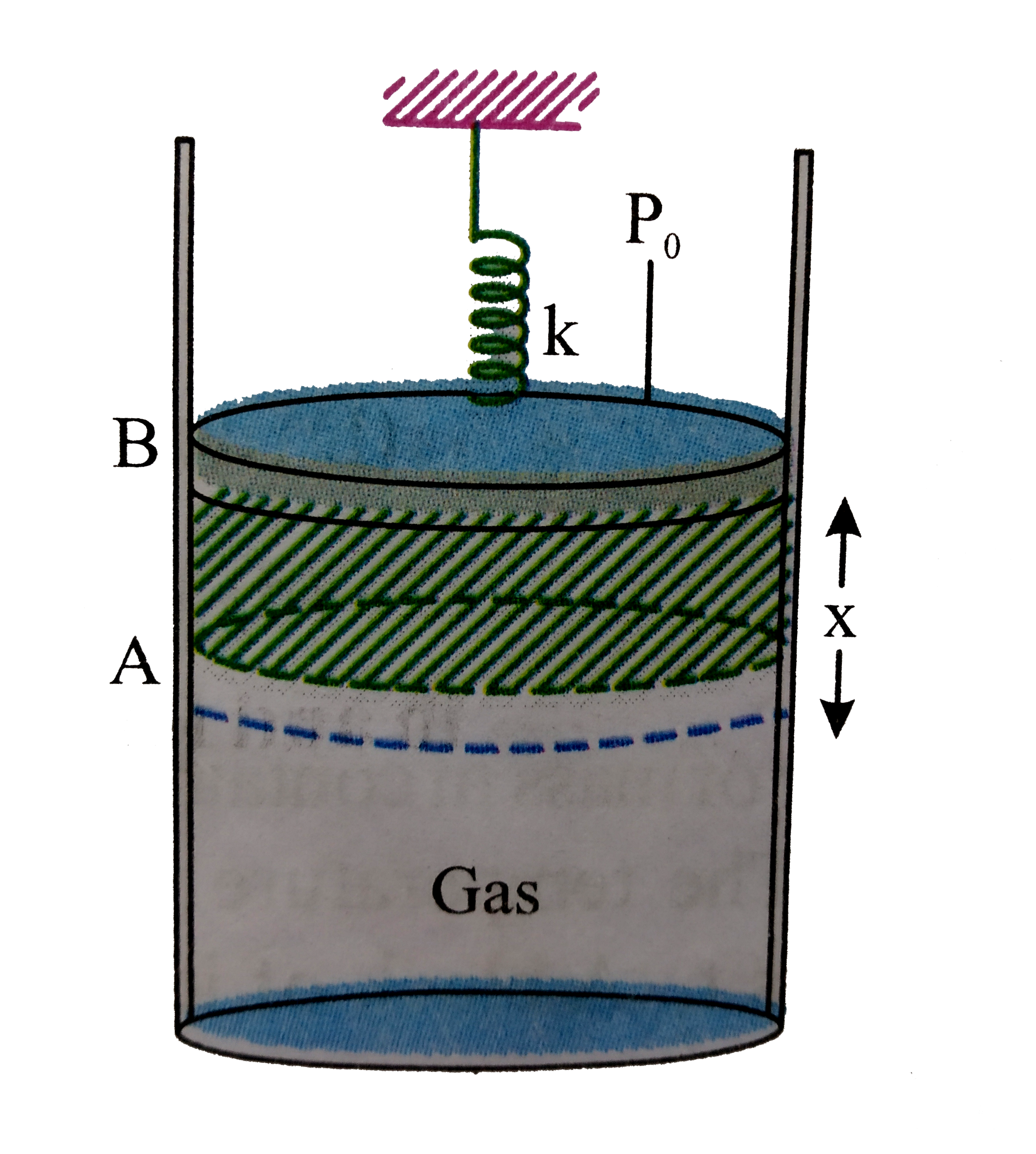
Change in internal energy of the gas isView SolutionTwo mole of an ideal monatomic gas are confined within a cylinder by a mass less spring loaded with a frictionless piston of negligible mass and crossectional area 4×10−3m2. The gas is heated by a heater for some time. During this time the gas expands and does 50J of work in moving the piston through a distance of 0.01m. The temperature of gas increases by 50k.
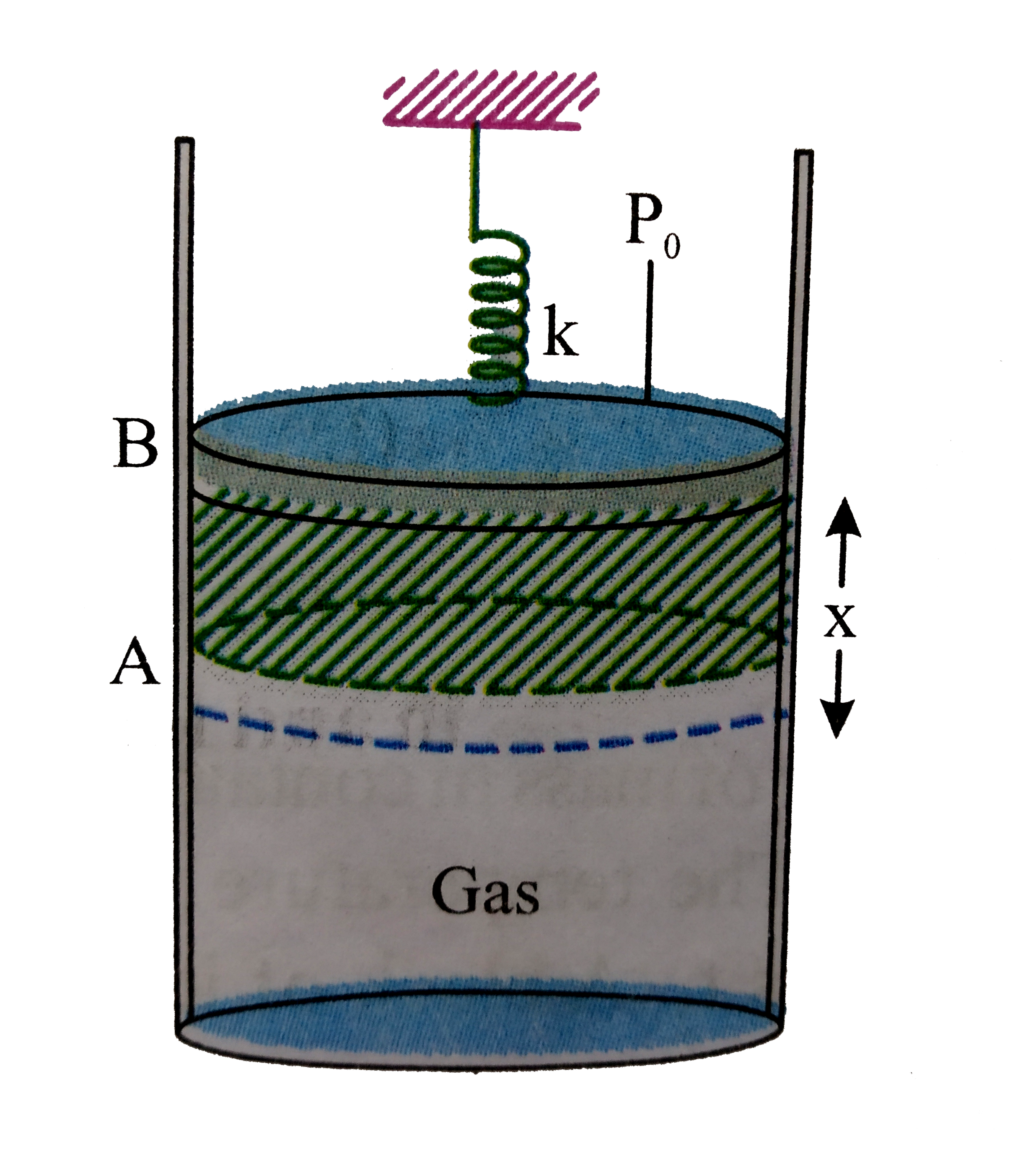
The force constant of spring isView Solution

