Calculation the flux through the flat disk held perpendicular to the end of a semi-infinite wire of charge per unit length l. The radius of the disk is R
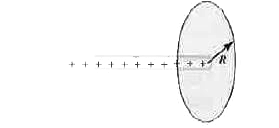
As can be easily seen, E1 is parallel to the surface of the disk at all the points. So, the angle between d→AandE⊥ is 90∘ at all the points. So, the flux due to E⊥ at all the points of the disk is
dϕ=→E⊥.d→A=E⊥dAcos90∘=0.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - CHECKPOINT7videos
GAUSS' LAW
- BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - PROBLEMS42videos
GAUSS' LAW
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)1videos
FORCE AND MOTION-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFLECTION EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
GEOMETRICAL OPTICS : REFLECTION
Similar Questions
Calculate the potential due to a thin charged rod of length L at the points along and perpendicular to the length. Charge per unit length on the rod is λ.
 View Solution
View SolutionCalculate the potential due to a thin charged rod of length L at the points along and perpendicular to the length. Charge per unit length on the rod is λ.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Consider the following four objects:
(i) a hoop
(ii) a flat disk
(iii) a solid sphere
(iv) a hollow sphere
Each of the objects has mass M and radius R. The axis of rotation passes through the center of each object and is perpendicular to the plane of the hoop and the plane of the flat disk. Which object requires the largest torque to give it the same angular acceleration?AThe solid sphereBThe hollow sphereCThe hoopDThe flat disk - Question 2 - Select One
A wire is bent to form a semi circle such that the radius of the semicircle is R. The charge per unit length is λ. The total electric field at the centre will be
A2λ/πε0RBλ/2πε0RC2λ/πε0R2Dλ/πε20R - Question 3 - Select One
A unifrom solid disk of radius R and mass M is free to rotate on a frictionless pivot through a point on its rim. If the disk is released from rest in the position shown in figure. The speed of the lowest point on the disk in the dashed position is.
 .A4√Rg3B2√Rg3C√Rg3D3√Rg2
.A4√Rg3B2√Rg3C√Rg3D3√Rg2
Find the electric field intensity at a point P which is at a distance R (point lying on the perpendicular drawn to the wire at one of its end) from a semi-infinite uniformly charged wire. (Linear charge density = λ).
View SolutionFind the electric field intensity at a point P which is at a distance R (point lying on the perpendicular drawn to the wire at one of its end) from a semi-infinite uniformly charged wire. (Linear charge density = λ).
View SolutionA wire of linear charge density λ passes through a cuboid of length l, breadth b and height h(l>b>h) in such a manner that the flux through the cuboid is maximum. The position of the wire is now changed, so that the flux through the cuboid is minimum. The raito of maximum flux to minimum flux will be
View SolutionNear an infinitely large flat plate with a surface charge density o on each side, the field strength is** E=δ∈nδ, while the field produced by a point charge at a distance r frorn the chargo is Prove that for a uniformly charged disk with a surface charge density a (on each side), the electric field strength on the axis of the disk is the same as for an infinitely large flat plate if the distances arc small in comparison with the disk's radius R, and is the same as for a point charge if the distances are large ** Usually the value of the field strength given in textbooks is half the one given here, since there it is assumed that the charge is on a geometric plane
View SolutionA non-conducting disk of radius R is rotating about its own axis with constant angular velocity ω in a perpendicular uniform magnetic field B as shown in figure. The emf induced between centre and rim of disk is
 View Solution
View Solution

