Find the electric field intensity at a point P which is at a distance R (point lying on the perpendicular drawn to the wire at one of its end) from a semi-infinite uniformly charged wire. (Linear charge density = λ).
Field at point P is due to an elemental charge.
dq(=λdl)
dE=kdq(R2+l2)
The component along x-axis
dEx=kdqcosθ(R2+l2)=k(dq)R(R2+l2)3/2
∴Ex=∞∫014πε0λdlR(R2+l2)3/2⇒Ex=λ4πε0R
Similarly, Ey=∞∫014πε0λ(dl)l(R2+l2)3/2
∴Ey=λ4πε0R
∴E=√E2X+E2Y=λ2.√2πε0R,tanθ=EyEx
⇒θ=45∘

Similar Questions
find the electric field strength due to a point charge of 5μC at a distance of 80 cm from the charge.
View SolutionIntensity of electric field at a point at a perpendicular distance .r. from an infinite line charge, having linear charge density .λ. is given by :
View Solution(i) Two infinitely long line charges each of linear charge density λ are placed at an angle θ as shown in figure. Find out electric field intensity at a point P, which is at a distance x from point O along angle bisector of line charges.
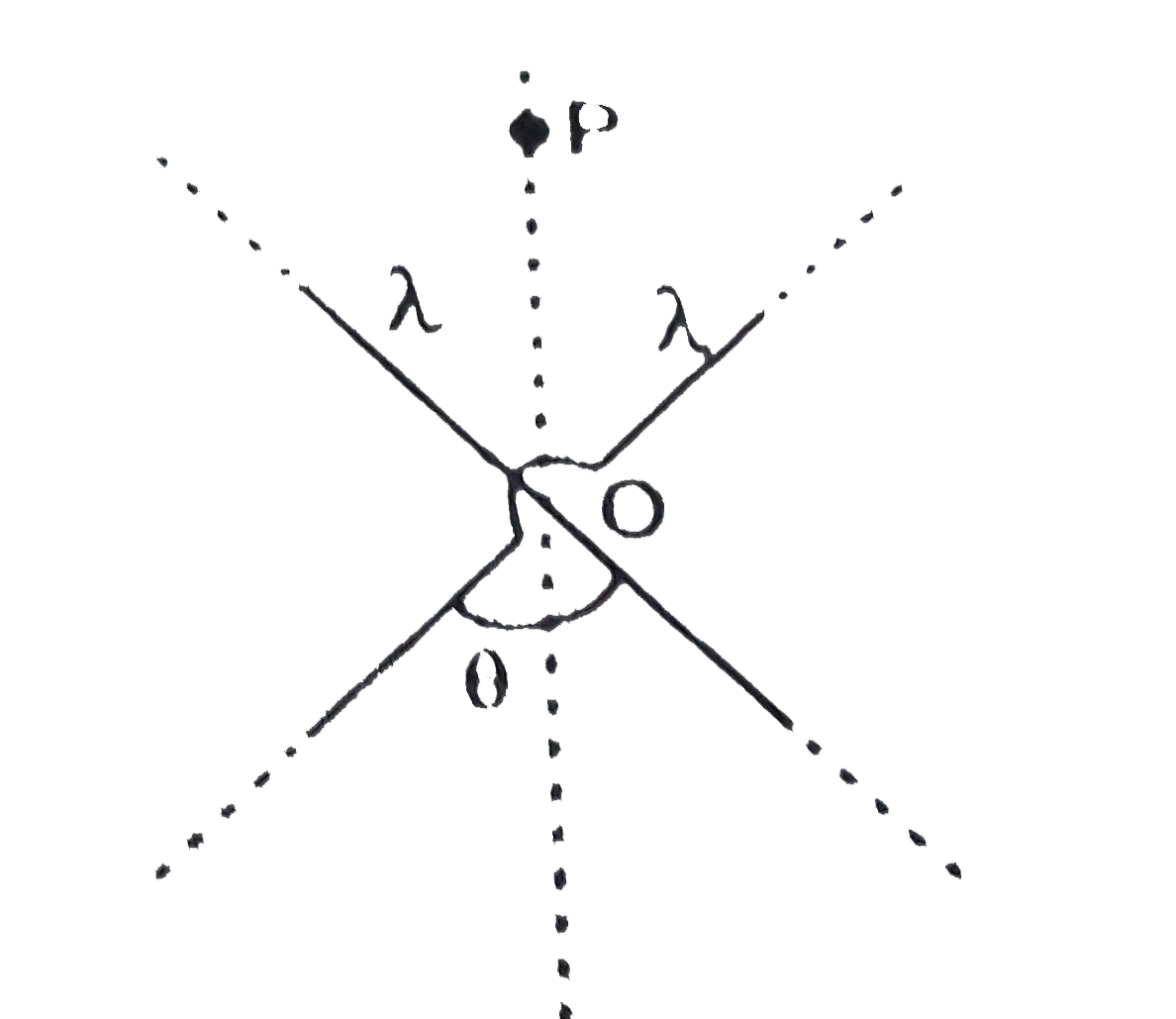
(ii) Repeat the above question if the line charge densities are λ and −λ. as shown in figure.

View SolutionIntensity of electric field at a point at a perpendicular distance .r. from an infinite line charge, having linear charge density .λ. is given by :
View SolutionFind the electric field at the centre of a uniformly charged semicircular ring of radius R. Linear charge density is λ
View SolutionWhat is the electric field intensity at any point on the axis of a charged rod of length 'L' and linear charge density λ? The point is separated from the nearer end by a.
View SolutionElectric field intensity at a point in between two parallel sheets with like charges of same surface charge densities (σ) is
View SolutionUsing Gauss’ law, derive an expression for the electric field at a point near an infinitely long straight uniformly charged wire.
View SolutionFind the electric field at point O, due to the segment of a ring, whose linear charge density is 8C/cm

View SolutionFind the electric field at a point P on the perpendicular bisector of a uniformly charged rod. The length of the rod is L, the charge on it is Q and the distance of P from the centre of the rod is a.
View Solution
