a nonconducting spherical shell of inner radius a=2.00 cm and outer radius b=2.40 cm has (within its thickness) a positive volume charge density ρ=A/r, where A is a constnat and r is the distance from the center of the shell. In addition, a small ball of charge q=45.0 fC is located at that center. What value should A have if the eletric field in the shell (a<b<c) is to be uniform ?

We solve for E:
E=14pε0[qr2g+2πA−2πAa2r2g]
Find the field to be uniform, the first and last terms in the brackets must cancel. They do if q−2πAa2=0orA=q/2πa2. With a=2.00×10−2m and q=45.0×10−15C, we have A=1.79×10−11C/m2.
The value we have found for A ensures the uniformity of the field strength inside the shell. Using the result found above, we can readily show that the clcctric field in the region a≤r≤b is
E=2πA4πε0=A2ε0
=1.79×10−11C/m22(8.85×10−12C2/N.m2)=1.01N/C.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - CHECKPOINT7videos
GAUSS' LAW
- BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - PROBLEMS42videos
GAUSS' LAW
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)1videos
FORCE AND MOTION-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFLECTION EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
GEOMETRICAL OPTICS : REFLECTION
Similar Questions
A spherical conducting shell of inner radius r1 and outer radius r2 has a charge Q.
(a) A charge q is placed at the centre of the shell. What is the surface charge density on the inner and outer surfaces of the shell ?View SolutionA conducting spherical shell having inner radius a and outer radius b carries a net charge Q. If a point charge q is placed at the centre of this shell, then the surface charge density on the outer surface of the shell is given as:
View Solution
Knowledge Check
- Question 1 - Select One
A point charge q is placed inside a conducting spherical shell of inner radius 2R and outer radius 3R at a distance of R from the center of the shell. Find the electric potential at the center of the shell.
A14πε0q2RB14πε04q3RC14πε05q6RD14πε02q3R
A metallic spherical shell has an inner radius R1 and outer radius R2. A charge is placed at the centre of the spherical cavity. The surface charge density on the inner surface is
 View Solution
View SolutionA metallic spherical shell has an inner radius R1 and outer radius R2. A charge is placed at the centre of the spherical cavity. The surface charge density on the inner surface is
 View Solution
View SolutionA conducting spherical shell of outer radius R and inner radius r = 3R/4 has no net charge on it. At its center there is a point charge q, and at a distance 2R from its center there is a point charge Q (Fig.) . (a) What is the magnitude of the electrostatic force on the charge q at the center due to the shell ? (b) What is the magnitude of net force on it?
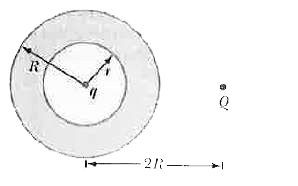 View Solution
View SolutionA point charge +q is placed at the centre of a conducting spherical shell of inner radius a and outer radius b. Find the charge appearing on the inner and outer surface of the shell.
View SolutionA point charge +q is placed at the centre of a conducting spherical shell of inner radius a and outer radius b. Find the charge appearing on the inner and outer surface of the shell.
View SolutionA metalic spherical shell has an inner radius R1and outer radius R2 . A charge Q is placed at the centre of the spherical cavity. What will be surface charge density on (i) the inner surface and (ii) the outer surface?
View SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d. The inner shell has total charge +2q and the outer shell has charge +4q.
(i) What is the total charge on the (a) inner surface of the small shell, (b) outer surface of the small shell (c) inner surface of the large shell, (d) outer surface of the large shell ?
(ii) Calculate the electric field in terms of q and the the distance r from the common centre of two shells for (a) r<a, (b) a<r<b, (c) b<r<c, (d) c<r<d, (e) r>d
 View Solution
View Solution

