An electron is releaed from the surface of a uniformly and positively charged sphere (volume charge density r, fig) Show that the electron will exceute SHM and find its time period

Text Solution

Verified by Experts

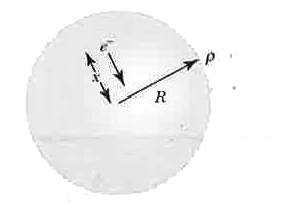
Since the electron will be negatively charged, it will be pulled by the positively charged sphere. The condition for the simple harmonic motion (SHM) is that the force should be proportional to the displacement x from the mean position.
At a distance x from the center, the face
$F = - e E = - \frac{ρ x}{3 ε_{0}}$
Since this force is proportional to distance x from the mean position (center) and directed toward it, the motion should be simple harmonic. Solving this, we get
$a = \frac{- e ρ}{3 m ε_{0}} x .$
But in an SHM,
$a = - ω^{2} x, ω = \sqrt{\frac{e ρ}{3 m ε_{0}}}, T = 2 π \sqrt{\frac{3 m ε_{0}}{e ρ}}$
Here the electron was moving along the diameter. Suppose that this electron was allowed to move only along a chord, starting from rest. In that case also the motion of the electron will be simple harmonic. A component of the force will be balanced by the walls of the tunnel in which electron moves. The net force will come out to be proportional to the distance from the center of the chord which will be the mean position in this case. Even the time period will come out to be the same

Updated on:21/07/2023