An insulating solid sphere of the radius R is charged in a non - uniform manner such that the volume charge density ρ=Ar, where A is a positive constant and r is the distance from the centre. The potential difference between the centre and surface of the sphere is
AR8ε0
AR4ε0
ARε0
AR2ε0
The correct Answer is:D
To find the potential difference between the center and the surface of an insulating solid sphere with a non-uniform charge density given by ρ=Ar, we can follow these steps:
Step 1: Understand the Charge Density
The charge density ρ is given as ρ=Ar, where A is a constant and r is the distance from the center of the sphere. This indicates that the charge density decreases as we move away from the center.
Step 2: Calculate the Charge Element
To find the electric field, we need to calculate the charge dq in a thin spherical shell of radius r and thickness dr. The volume of this shell is:
dV=4πr2dr
Thus, the charge dq in this shell can be expressed as:
dq=ρ⋅dV=(Ar)⋅(4πr2dr)=4πArdr
Step 3: Calculate the Total Charge Enclosed
To find the electric field at a distance r from the center, we need to consider the total charge Qenc enclosed within a sphere of radius r:
Qenc=∫r0dq=∫r04πAr′dr′=4πA((r′)22)r0=2πAr2
Step 4: Apply Gauss's Law
Using Gauss's law, we know that the electric field E at a distance r from the center is given by:
Φ=E⋅A=Qencϵ0
where A=4πr2 is the surface area of the sphere. Thus, we have:
E⋅4πr2=2πAr2ϵ0
From this, we can solve for E:
E=2A4ϵ0=A2ϵ0
Step 5: Calculate the Potential Difference
The potential difference V between the center and the surface of the sphere can be calculated using the relationship:
ΔV=−∫0REdr
Substituting the expression for E:
ΔV=−∫0RA2ϵ0dr=−(A2ϵ0r)0R=−(0−AR2ϵ0)=AR2ϵ0
Final Answer
Thus, the potential difference between the center and the surface of the sphere is:
ΔV=AR2ϵ0
The charge density ρ is given as ρ=Ar, where A is a constant and r is the distance from the center of the sphere. This indicates that the charge density decreases as we move away from the center.
To find the electric field, we need to calculate the charge dq in a thin spherical shell of radius r and thickness dr. The volume of this shell is:
dV=4πr2dr
Thus, the charge dq in this shell can be expressed as:
dq=ρ⋅dV=(Ar)⋅(4πr2dr)=4πArdr
To find the electric field at a distance r from the center, we need to consider the total charge Qenc enclosed within a sphere of radius r:
Qenc=∫r0dq=∫r04πAr′dr′=4πA((r′)22)r0=2πAr2
Using Gauss's law, we know that the electric field E at a distance r from the center is given by:
Φ=E⋅A=Qencϵ0
where A=4πr2 is the surface area of the sphere. Thus, we have:
E⋅4πr2=2πAr2ϵ0
From this, we can solve for E:
E=2A4ϵ0=A2ϵ0
The potential difference V between the center and the surface of the sphere can be calculated using the relationship:
ΔV=−∫0REdr
Substituting the expression for E:
ΔV=−∫0RA2ϵ0dr=−(A2ϵ0r)0R=−(0−AR2ϵ0)=AR2ϵ0
Thus, the potential difference between the center and the surface of the sphere is:
ΔV=AR2ϵ0
Similar Questions
A solid non conducting sphere of radius R has a non-uniform charge distribution of volume charge density, ρ=ρ0rR, where ρ0 is a constant and r is the distance from the centre of the sphere. Show that : (i) the total charge on the sphere is Q=πρ0R3 (ii) the electric field inside the sphere has a magnitude given by, E=KQr2R4
View SolutionA solid sphere of radius R has a charge Q distributed in its volume with a charge density ρ=kra, where k and a are constants and r is the distance from its centre. If the electric field at r=R2 is 18 times that r=R, find the value of a.
View Solution
Knowledge Check
A system consits of a uniformly charged sphere of radius R and a surrounding medium filled by a charge with the volume density ρ=αr, where α is a positive constant and r is the distance from the centre of the sphere. Find the charge of the sphere for which the electric field intensity E outside the sphere is independent of R.
Aα2ε0B2αε0C2παR2DNone of these
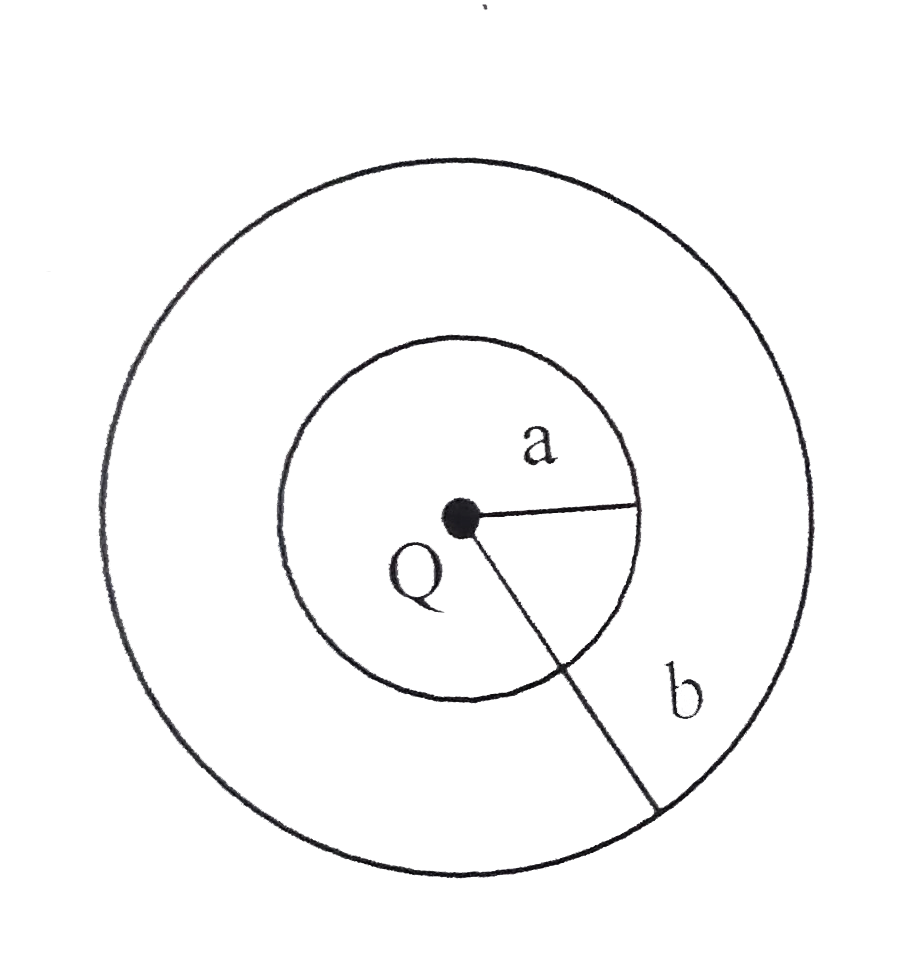
The region between two concentric spheres of radii 'a' and 'b', respectively (see figure), have volume charge density ρ=Ar, where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is:
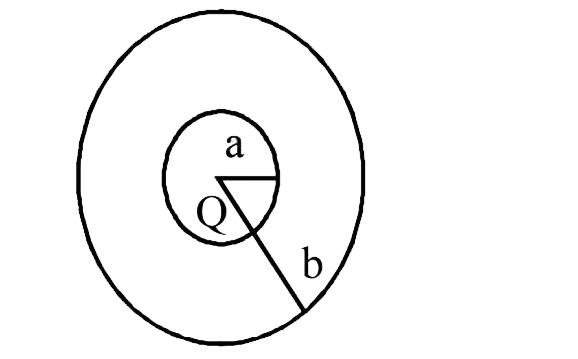
View SolutionThe region between two concentric spheres of radii ‘a’ and ‘b’, respectively (see figure), has volume charge density p=Ar, where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is :
View SolutionAn insulating solid sphere of radius R has a uniformly positive charge density ρ. As a result of this uniform charge distribution there is a finite value of electric potential at the centre of the sphere, at the surface of the sphere and also at a point out side the sphere. The electric potential at infinity is zero.
Statement-1: When a charge 'q' is taken from the centre to the surface of the sphere, its potential energy changes by qρ3∈0
Statement-2 : The electric field at a distance r(r<R) from the centre of the the sphere is ρr3∈0
View SolutionA solid sphere of radius R1 and volume charge density ρ=ρ0r is enclosed by a hollow sphere of radius R2 with negative surface charge density σ, such that the total charge in the system is zero . ρ0 is positive constant and r is the distance from the centre of the sphere . The ratio R2/R1 is
View SolutionTwo non-conducting solid spheres of radii R and 2R, having uniform volume charge densities ρ1 and ρ2 respectively, touch each other. The net electric field at a distance 2R from the centre of the smaller sphere, along the line joining the centres of the spheres, is zero. The ratio ρ1ρ2 can be
View SolutionA solid sphere of radius R is charged uniformly through out the volume. At what distance from its surface is the electric potential 1/4 of the potential at the centre?
View SolutionA sphere of radius R carries charge such that its volume charge density is proportional to the square of the distance from the centre. What is the ratio of the magnitude of the electric field at a distance 2 R from the centre to the magnitude of the electric field at a distance of R/2 from the centre?
View Solution